信息学奥赛初赛天天练-64-NOIP2017普及组-基础题3-逆序对、中缀表达式、后缀表达式、栈、链式栈、子序列、子串、十进制转R进制
PDF文档公众号回复关键字:20240814

NOIP 2017 普及组 基础题3
11 对于给定的序列 {ak},我们把 (i,j) 称为逆序对当且仅当 i<j 且 ai>aj。那么序列 1,7,2,3,5,4 的逆序对数为( )个
A 4
B 5
C 6
D 7
12 表达式 a * (b + c) * d 的后缀形式是( )
A a b c d * + *
B a b c + * d *
C a * b c + * d
D b + c * a * d
13 向一个栈顶指针为hs 的链式栈中插入一个指针s 指向的结点时,应执行( )
A hs->next = s;
B s->next = hs; hs = s;
C s->next = hs->next; hs->next = s;
D s->next = hs; hs = hs->next;
14 若串 S=copyright,其子串的个数是( )
A 72
B 45
C 46
D 36
15 十进制小数 13.375 对应的二进制数是( )
A 1101.011
B 1011.011
C 1101.101
D 1010.01
2 相关知识点
1) 逆序对
逆序对是组合数学和算法中的一个概念,它用于衡量一个序列中两个元素的位置关系。在一个给定的序列中,如果前面的元素大于后面的元素,那么这两个元素就构成了一个逆序对。
例如,在序列 [3, 1, 4, 2] 中,逆序对有 (3, 1), (3, 2), (4, 2),总共有 3 个逆序对。
逆序对的数量可以用来衡量序列的有序程度。在一个完全有序的序列中,逆序对的数量为 0;在一个完全逆序的序列中,逆序对的数量为 n(n-1)/2,其中 n 是序列的长度
2) 中缀表达式转后缀表达式
确定优先级,按优先级逐一处理操作符(把操作符从操作数中间移到操作数后边)
例如如下中缀表达式转为后缀表达式
1 + ( 2 + 3)* 4 ) – 5
// 按优先级对表达式数字加括号
((1 + (( 2 + 3)* 4 )) – 5 )
//从最里面的一层括号开始运算,转换成后缀表达式
//转换方法,去除括号,数字在前,顺序不变,操作符移到最后
1. ( 2 + 3) => 2 3 +
// ( 2 + 3)可以看作一个整体x
2. (( 2 + 3)* 4 ) => (x+4) => x 4 + => 2 3 + 4 *
//(( 2 + 3)* 4 )看作一个整体x
3. (1 + (( 2 + 3)* 4 ))=> (1+x)=>1 x + = 1 2 3 + 4 * +
// (1 + (( 2 + 3)* 4 )) 看作一个整体x
4. ((1 + (( 2 + 3)* 4 )) – 5 ) =>(x-5)=>x 5 - => 1 2 3 + 4 * + 5 -
所以转换后的后缀表达式为 1 2 3 + 4 * + 5 -
3) 栈
栈又名堆栈,是一种限定仅在表尾进行插入和删除操作的线性表,这一端称为栈顶,另一端称为栈底
栈中的数据元素遵守后进先出的原则
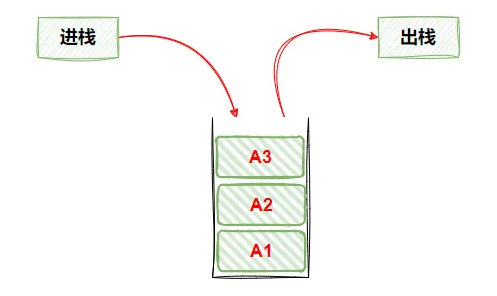
链式栈
链栈是指采用链式存储结构实现的栈,通常链栈用单链表表示
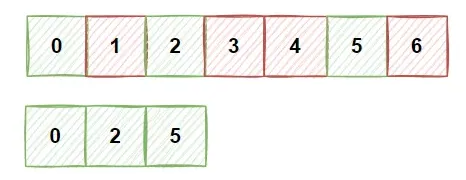
4) 子序列
一个给定的序列的子序列,就是将给定序列中零个或多个元素去掉之后得到的结果
例如
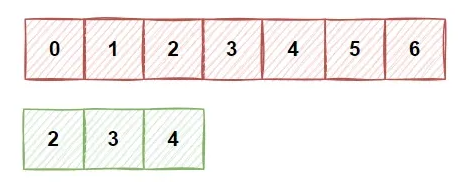
子串
给定串中任意个连续的字符组成的子序列称为该串的子串
5) 十进制转R进制
十进制整数转R进制
将十进制整数转换为 R 进制整数的方法是通过不断地将该整数除以 R,然后取余数,直到商为 0。将得到的余数按照从后往前的顺序排列,就得到了 R 进制表示的整数

十进制小数转R进制
将十进制小数转换为 R 进制小数的方法是通过不断地将该小数乘以 R,然后取整数部分,直到小数部分为 0 或达到所需的精度。将得到的整数部分按照从前往后的顺序排列,就得到了 R 进制表示的小数

3 思路分析
11 对于给定的序列 {ak},我们把 (i,j) 称为逆序对当且仅当 i<j 且 ai>aj。那么序列 1,7,2,3,5,4 的逆序对数为( B )个
A 4
B 5
C 6
D 7
分析
根据逆序对的定义,前面比后面大的一对数称为逆序对
给定的序列从头开始每2个数进行枚举
1开头,后面没有比1小的
7开头 (7,2),(7,3),(7,5),(7,4) 总共4个
2开头,后面没有比2小的
3开头,后面没有比3小的
5开头,(5,4) 1个
总共逆序对为4+1=5
12 表达式 a * (b + c) * d 的后缀形式是( B )
A a b c d * + *
B a b c + * d *
C a * b c + * d
D b + c * a * d
分析
中缀表达式转后缀,根据优先级加括号,然后逐一去括号
a * (b + c) * d 加括号后 ((a * (b + c)) * d)
(b + c) -- bc+
//把bc+看作x 继续去括号
(a * (b + c)) -- (a * x) -- ax* 用bc+替换 x -- abc+*
//看作 x
((a * (b + c)) * d) -- x*d -- xd* 用abc+*替换x -- abc+*d*
所以选B
13 向一个栈顶指针为hs 的链式栈中插入一个指针s 指向的结点时,应执行( B )
A hs->next = s;
B s->next = hs; hs = s;
C s->next = hs->next; hs->next = s;
D s->next = hs; hs = hs->next;
分析
A hs—>next指向s,栈顶的下一个节点为s,把s插入栈顶下面,不符合要求
B s->next=hs ,s的下一个节点指向栈顶元素,把栈顶下移,hs=s ,栈顶指针指向s,这样s成为新栈顶,符合要求
C s->next = hs->next,s的下一节点指向栈顶的下一个节点,hs->next = s 栈顶的下一个节点指向s,说明s插入到栈顶下面,不符合要求
D s->next = hs,s的下一个节点指向栈顶元素,hs = hs->next 栈顶指针指向栈顶的下一个节点,s没被插入到栈中,不符合要求
14 若串 S=copyright,其子串的个数是( C )
A 72
B 45
C 46
D 36
分析
空串 1个
1个字符 9个
2个字符 8个
3个字符7个
4个字符6个
5个字符5个
6个字符4个
7个字符3个
8个字符2个
9个字符1个
1+2+3...+9=(1+9)*9/2=45
再加1个空串45+1=46个
15 十进制小数 13.375 对应的二进制数是( A )
A 1101.011
B 1011.011
C 1101.101
D 1010.01
分析
十进制整数转二进制
整除法
13/2=6...1
6/2 =3...0
3/2 =1...1
1/2 =0...1
从下到上排列余数,1101
小数部分转二进制
0.375 * 2=0.75 整数为0 -- 0
0.75 * 2=1.5 整数为1 -- 1 ,1.5去1后变成0.5
0.5 * 2=1 正数为1 -- 1
从上到下取整数 011
整数部分和小数部分排列
1101.011
作者:newcode 更多资源请关注纽扣编程微信公众号

从事机器人比赛、机器人等级考试、少儿scratch编程、信息学奥赛等研究学习





