信息学奥赛初赛天天练-59-NOIP2018普及组-基础题3-同时取最大和最小、集合计数、质数与互质、特殊位运算、栈

PDF文档公众号回复关键字:20240808

NOIP2018 基础题3

单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

9 给定一个含 N 个不相同数字的数组，在最坏情况下，找出其中最大或最小的 数，至少需要N−1 次比较操作。则最坏情况下，在该数组中同时找最大与 最小的数至少需要( )次比较操作。
( ⌈⌉ 表示向上取整，⌊⌋ 表示向下取整）
A ⌈3N/2⌉ - 2
B ⌊3N/2⌋ - 2
C 2N-2
D 2N-4

12 设含有10个元素的集合的全部子集数为S，其中由 7 个元素组成的子集数为 T，则 T/S 的值为( )
A 5/32
B 15/128
C 1/8
D 21/128

13 10000 以内，与 10000 互质的正整数有( )个
A 2000
B 4000
C 6000
D 8000

14 为了统计一个非负整数的二进制形式中 1 的个数，代码如下：

int CountBit(int x)
{
	int ret = 0;
	while (x)
	{
		ret++;
		___________;
	}
	return ret;
}

则空格内要填入的语句是( )

A x>>=1
B x &= x-1
C x |=x>>1
D x<<=1

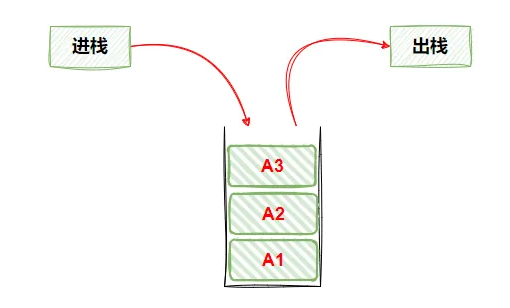
15 下图中所使用的数据结构是

A 哈希表
B 栈
C 队列
D 二叉树

2 相关知识点

1) 比较找最大

冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端

n个元素的冒泡排序，需要n趟完成，

每趟进行逐一两两比较，进行n-1次比较，把最大(最小)元素比较出来，交换到最后

如果同时取最大和最小，

可以定义2个变量，最大max和最小min，然后循环去找2个数，假设i为2，比较大小，得到max1和min1，然后max1和max比较，min1和min比较，总共比较3次

然后循环步长为2，i+=2，此时i=2，循环进行N/2次

所以总的比较次数为3*N/2次

2) 集合计数

集合中的元素，要么出现，要么不出现，因此n个元素的集合所有子集数(包括空集合)为n个2相乘，2^n

集合本身没有顺序，因此其中m个元素的子集为C(n,m)

3) 质数与互质

质数 -素数

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）

互质

若N个整数的最大公因数是1，则称这N个整数互质

例如

3和5的最大公约数是1，所以3和5是互质

8和10的最大公约数是2，不是1，因此8和10不是互质

4) x&=x-1

x&=x-1 去除二进制补码最后1个1

示例代码

#include<bits/stdc++.h>
using namespace std;
/*
  去除二进制补码最后一个1
  正数 
  9对应补码 0000 1001 
  8对应补码 0000 1000 
  x&=x-1;
  0000 1001 
& 0000 1000 
-------------
  0000 1000
结果为10进制的8
 负数
 -9
 原码  1000 1001
 反码  1111 0110
 补码  1111 0111
 x-1 -9-1=-10
 原码  1000 1010
 反码  1111 0101
 补码  1111 0110
 x&=x-1;
  1111 0111
& 1111 0110 
-------------
  1111 0110 
  比-9的补码 1111 0111少了末尾的1
  补码 1111 0110  对应反码 1111 0101 对应原码 1000 1010 对应十进制-10 
*/ 
int main(){
	int x=9;
	//去除二进制补码最后1个1 
	x&=x-1;
	cout<<x<<endl;//输出 8 
	
	x=-9;
	//去除二进制补码最后1个1 
	x&=x-1;
	cout<<x<<endl;//输出 -10 
	return 0;
}

5) 栈

栈又名堆栈，是一种限定仅在表尾进行插入和删除操作的线性表，这一端称为栈顶，另一端称为栈底

栈中的数据元素遵守后进先出的原则

3 思路分析

9 给定一个含 N 个不相同数字的数组，在最坏情况下，找出其中最大或最小的 数，至少需要N−1 次比较操作。则最坏情况下，在该数组中同时找最大与 最小的数至少需要( A )次比较操作。
( ⌈⌉ 表示向上取整，⌊⌋ 表示向下取整）
A ⌈3N/2⌉ - 2
B ⌊3N/2⌋ - 2
C 2N-2
D 2N-4

分析

如果分别找最大值、最小值，则至少都需要N-1次操作。
同时找最大最小值，按照下面的优化算法
N为奇数，最大值、最小值的初始值都设为第一个元素
枚举，从第2个元素开始，每次两个元素 (循环步长为2)，1)比较1次找最大和最小，2)找到最大值和当前最大值比较，3)找到最小值和当前最小值比较
除去第1个元素，循环 (N-1)/2次比较，总共比较3*(N-1)/2=3N+1/2-2

N为偶数时，前2个数比较1次，查出最大，最小
枚举，从第3个元素开始，每次两个元素 (循环步长为2), 1)比较1次找最大和最小，2)找到最大值和当前最大值比较，3)找到最小值和当前最小值比较
除去前2个元素，循环 (N-2)/2次比较，上面3种情况总共比较3*(N-2)/2再加上第1次前2个数比较的1次
3*(N-2)/2+1=3N/2-3+1=3N/2-2
N为奇数时，3N/2自动向下取整 例如3*3/2=4 实际比较次数应该向上取整，⌈3N/2⌉=3N+1/2 所以3N+1/2=⌈3N/2⌉-2  
N为偶数时，3N/2正好可以整除，和向上取整的值相同，也可以表示成：⌈3N/2⌉，所以比较次数为⌈3N/2⌉-2

12 设含有10个元素的集合的全部子集数为S，其中由 7 个元素组成的子集数为 T，则 T/S 的值为( B )
A 5/32
B 15/128
C 1/8
D 21/128

分析

S为10个元素的集合，每个元素可以在集合和不在集合2种情况，根据乘法原理 10个2相乘，为2^10=1024
T为10个元素取其中7个元素组成的子集，表示从10个元素中任意取7个没有顺序，C(10,7)=C(10,3)=10*9*8/3/2/1=120
T/S=120/1024=15/128

13 10000 以内，与 10000 互质的正整数有( B )个
A 2000
B 4000
C 6000
D 8000

分析

互质表示与10000没有公约数，即不能被10000的质因数整除
10000=10^4=2^4*5^4
10000/2=5000，10000以内有质因数2的数有5000个
10000/5=2000，10000以内有质因数5的数有2000个
10000/10=1000，同时有质因数2和5的数有1000个
能被2和5整除的数有5000+2000-1000=6000个
所以互质的数为10000-6000=4000个

14 为了统计一个非负整数的二进制形式中 1 的个数，代码如下：

int CountBit(int x)
{
	int ret = 0;
	while (x)
	{
		ret++;
		___________;
	}
	return ret;
}

则空格内要填入的语句是( B )

A x>>=1
B x &= x-1
C x |=x>>1
D x<<=1

x &= x-1 表示去除最右边的1
每次循环去除1个最右边的1，累计ret加1
直到去除完结束

15 下图中所使用的数据结构是( B )

A 哈希表
B 栈
C 队列
D 二叉树

图中B后进先出，可以看出是栈
A 进  B 进  B 出 C进