信息学奥赛初赛天天练-44-CSP-J2020基础题-排列组合、乘法原理、捆绑法、隔板法、排除法示例及应用

信息学奥赛初赛天天练-44-CSP-J2020基础题-排列组合、乘法原理、捆绑法、隔板法、排除法示例及应用

PDF文档公众号回复关键字:20240711

2020 CSP-J 选择题

单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

10.有5 个小朋友并排站成一列，其中有两个小朋友是双胞胎，如果要求这两个双胞胎必须相邻，则有（ ）种不同排列方法?

A.48

B.36

C.24

D.72

13.干支纪年法是中国传统的纪年方法，由10个天干和12个地支组合成60个天干地支。由公历年份可以根据以下公式和表格换算出对应的天干地支。
天干 =（公历年份）除以10所得余数
地支 =（公历年份）除以12所得余数

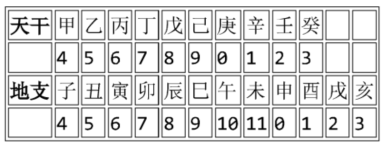
例如，今年是 2020 年，2020 除以 10 余数为 0，查表为"庚”；2020 除以 12，余数为 4，查表为“子” 所以今年是庚子年。
请问 1949 年的天干地支是（ ）

A.己酉

B.己亥

C.己丑

D.己卯

14.有10 个三好学生名额分配到 7 个班级，每个班级至少有一个名额，一共有（ ）种不同的分配方案

A.84

B.72

C.56

D.504

15.有五副不同颜色的手套（共 10 只手套，每副手套左右手各 1 只），一次性从中取 6 只手套，请问恰好能配成两副手套的不同取法有（ ）种

A.120

B.180

C.150

D.30

2 相关知识点

1) 乘法原理

做一件事，完成它需要分成n个步骤，做第一 步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法。

那么完成这件事共有 N=m1 * m2 * m3 …* mn 种不同的方法

每个步骤没有完成一件事，只是完成了其中一个步骤

例如

马戏团的小丑有红、黄、蓝三顶帽子和黑、白两双鞋，他每次出场演出都要戴一顶帽子、穿一双鞋。问：小丑的帽子和鞋共有几种不同搭配?

分析

演出前着装需要2步

第1步 选1顶帽子 ，有3种选法

第2步 选1双鞋子 ，有2种选法

分2步适合乘法原理，总共搭配数 3 * 2 =6 种

2) 捆绑法

排列组合中的相邻问题可以通过捆绑法来解决。

这种方法的基本思路是，将要求相邻的元素视为一个整体（即一个“大元素”），然后与其他元素一起进行排列。同时，需要注意这个“大元素”内部元素的排列

具体步骤如下：

将要求相邻的元素捆绑在一起，视为一个整体。

将这个整体与其他元素一起进行全排列。

考虑这个整体内部元素的排列。由于它们是相邻的，所以需要考虑它们之间的相对顺序

例题1

5个男生和3个女生排成一排，3个女生必须排在一起，有多少种不同排法?( )

A. 240 B. 320 C. 450 D. 4320

答案 D

分析

3个女生必须在一起，采用捆绑法，把3个女生捆绑在一起当作一个元素

第1步

把3个女生视为一个元素，与5个男生进行排列,共有 A(6,6)=6 * 5 * 4 * 3 *2 * 1=720

第2步

3个女生内部再进行排列，A(3,3) = 3 * 2 * 1=6

需要2步完成，需采用乘法原理对2步排列数进行相乘：720 * 6 = 4320种

2) 隔板法

将n个相同元素分给m个不同对象，要求元素全部分完，且每个对象至少分一个元素的问题

在n个元素之间的n-1个空中插入m-1个板，可以把n个元素分成m组的方法

总共有 C(n-1,m-1)种

n-1是n个元素之间有n-1个空，m-1是m-1个板可以分成m组

例题

现有7个一样的苹果，要分给3个小朋友，每人至少分1个，请问有多少种分法?

分析

7个一样的苹果，要分给3个小朋友，即7个一样的苹果分成3组，在7个苹果形成的6个空中，插入2个隔板即可

C(6,2)=6 * 5 /(2 * 1) = 15 种

排除法

当符合条件的情况繁杂而不符合条件的情况单一时，适合将不符合条件的情况从所有情况中减去

例题

从6名男生，5名女生中任选4人参加竞赛，要求男女至少各1名，有多少种不同的选法?

A.240 B.310 C.720 D.1080

分析

男女至少各一人的反面就是分别只选男生或者女生，这样就可以变化成C(11，4)-C(6，4)-C(5，4)=310

3 思路分析

10.有5 个小朋友并排站成一列，其中有两个小朋友是双胞胎，如果要求这两个双胞胎必须相邻，则有（ A ）种不同排列方法?

A.48

B.36

C.24

D.72

分析

第1步

双胞胎必须相邻，使用捆绑法，需要把双胞胎捆绑在一起当作一个，和其他3个做排列组合

A(4,4)

第2步

双胞胎内部有顺序，A在左，B在右或者A在右B在左

A(2,2)

根据乘法原理 A(4,4) * A(2,2) = 4 * 3 * 2 * 1 * 2 *1 = 48

13.干支纪年法是中国传统的纪年方法，由10个天干和12个地支组合成60个天干地支。由公历年份可以根据以下公式和表格换算出对应的天干地支。
天干 =（公历年份）除以10所得余数
地支 =（公历年份）除以12所得余数

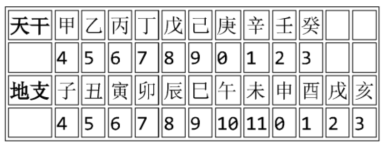
例如，今年是 2020 年，2020 除以 10 余数为 0，查表为"庚”；2020 除以 12，余数为 4，查表为“子” 所以今年是庚子年。
请问 1949 年的天干地支是（ C ）

A.己酉

B.己亥

C.己丑

D.己卯

分析

天干：1949%10 = 9 对应 己

地支：1949%12 = 5 对应 丑

所以1949 年的天干地支是 己丑

14.有10 个三好学生名额分配到 7 个班级，每个班级至少有一个名额，一共有（ A ）种不同的分配方案

A.84

B.72

C.56

D.504

分析

相同名额分给不同的班级，每班至少有一个名额，使用隔板法，分成7个班级，分成7组，需要6个隔板

6个隔板可以放到9个空中

C(9,6)=C(9,3)=9 * 8 * 7 /(3 * 2 * 1) = 84

15.有五副不同颜色的手套（共 10 只手套，每副手套左右手各 1 只），一次性从中取 6 只手套，请问恰好能配成两副手套的不同取法有（ A ）种

A.120

B.180

C.150

D.30

分析

第1步

从5副不同颜色的手套中选2副

C(5,2)=5*4 /2=10

第2步

需要选择6只，还差2只，从剩余6只手套中选2只

C(6,2)=6 * 5 /2 =15

由于第1步已经选择好了2副手套，所以此步选择的不能是1副，排除是1副的情况，共有3种情况

15-3=12

根据乘法原理 10 * 12=120