信息学奥赛初赛天天练-38-CSP-J2021阅读程序-约数个数、约数和、埃氏筛法、欧拉筛法筛素数应用

PDF文档公众号回复关键字:20240628

2021 CSP-J 阅读程序3

1阅读程序(判断题1.5分选择题3分共计40分 )

01 #include<stdio.h>
02 using namespace std;
03
04 #define n 100000
05 #define N n+1
06 
07 int m;
08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];
10 
11 void init()
12 {
13	 f[1]=g[1]=1;
14	 for(int i=2;i<=n;i++){
15	 	if(!a[i]){
16			b[m++]=i;
17			c[i]=1,f[i]=2;
18			d[i]=1,g[i]=i+1;
19		}
20		for(int j=0;j<m&&b[j]*i<=n;j++){
21			int k=b[j];
22			a[i*k]=1;
23			if(i%k==0){
24				c[i*k]=c[i]+1;
25				f[i*k]=f[i]/c[i*k]*(c[i*k]+1);
26				d[i*k]=d[i];
27				g[i*k]=g[i]*k+d[i];
28				break;
29			}
30			else{
31				c[i*k]=1;
32				f[i*k]=2*f[i];	
33				d[i*k]=g[i];
34				g[i*k]=g[i]*(k+1);
35			}
36		}
37	 }
38 }
39
40 int main()
41 {
42	 init();
43	
44	 int x;
45	 scanf("%d",&x);
46	 printf("%d %d\n",f[x],g[x]);
47	 return 0;
48 }

假设输入的x是不超过1000的自然数，完成下面的判断题和单选题

判断题

28.若输入不为"1"，把第13删去不会影响输出的结果( )

29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( )

30.(2分)在执行完init()后，f数组不是单调递增的，但g数组是单调递增的( )

单选题

31.init 函数的时间复杂度为( )

A. O(n)

B. O(nlogn)

C. O(n sqrt(n))

D. O(n^2)

32.在执行完init()后，f[1],f[2],f[3]...... f[100]中有( )个等于2.

A. 23

B. 24

C. 25

D. 26

33.(4分)当输入为"1000"时，输出为( )

A. "15 1340"

B. "15 2340"

C. "16 2340"

D. "16 1340"

2 相关知识点

埃式筛法

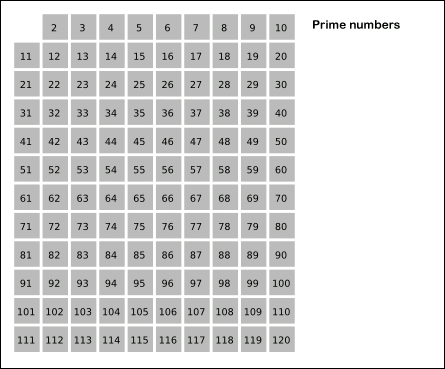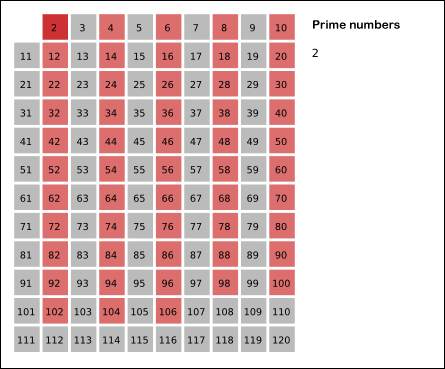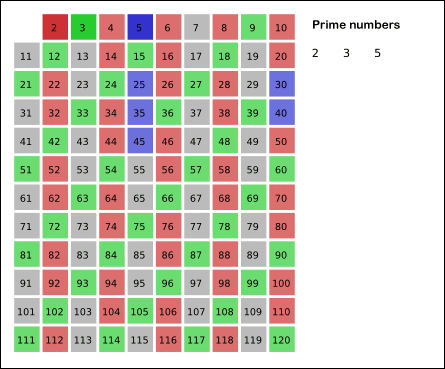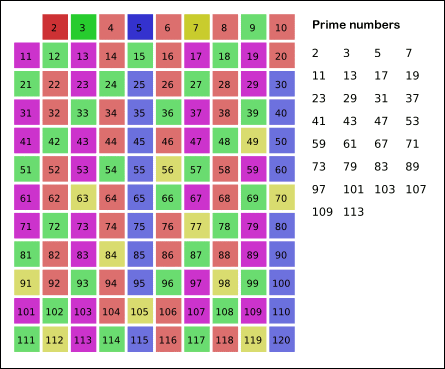
如果一个数是素数，那么它的倍数一定不是素数。我们要找n以内的所有素数，那么把n以内的合数全部筛掉，剩下的就是素数了

时间复杂度

O(n * log (log n) )

欧拉筛法

将合数分解为一个最小质数乘以另一个数的形式，即合数 = 最小质数 * 自然数，然后通过最小质数来判断当前数是否被标记过

时间复杂度

O(n)

3 思路分析

分析

本程序通过欧拉筛求约数个数及其约数和

使用到的对应数组

标记a数组，对合数进行标记，未标记的则是质数

质数表b数组，从小到大知道质数写到b数组

约数个数f数组，记录一个数对应的约数的个数

在填入约数个数f数组时，使用到最小质因数个数c数组

在填入约数和g数组时，使用到约数和对应的连乘积除第1项外的其他连乘积d数组

约数和g数组，记录一个数对应的约数之和

08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];

假设输入的x是不超过1000的自然数，完成下面的判断题和单选题

判断题

28.若输入不为"1"，把第13删去不会影响输出的结果( T )

分析

13行程序计算并未使用，只对f[1],g[1]输出有影响，如果不输出f[1],g[1]，不会影响输出

所以输入不为"1"，删除不影响输出结果

29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( F )

分析

c[i]表示i的最小质因数个数
f[i]表示i的约数个数，计算公式如下

H = p1^a1 * p2^a2 ....pn^an 其中 pi都是质数，ai是幂次，p1是最小的质数
约数的个数f[i]=(a1+1)*(a2+1)*...(an+1)
其中a1是最小质因数个数
c[i]表示i的最小质因数个数=a1
满足条件i%k==0
c[i*k]=相当于最小质数+1=a1+1
a1+1是f[i]的因子，所以f[i]/c[i*k]不会存在无法整除的情况
所以错误

30.(2分)在执行完init()后，f数组不是单调递增的，但g数组是单调递增的( F )

分析

f数组是约数个数，合数个数多，质数个数少，3 4 5 对应约数个数分别是2 3 2 看，并不是单调递增的

g数组是约数和，3 4 5 对应约数和分别是4 7 6 看，并不是单调递增的

单选题

31.init 函数的时间复杂度为( A )

A. O(n)

B. O(nlogn)

C. O(n sqrt(n))

D. O(n^2)

分析

此算法是欧拉筛法求质数，欧拉筛是线性筛法，即所有的合数都被它最小的质因子筛一次，减少了埃氏筛法的重复筛的次数，时间复杂度近似O(n)

32.在执行完init()后，f[1],f[2],f[3]...... f[100]中有( C )个等于2.

A. 23

B. 24

C. 25

D. 26

分析

f数组是约数个数，约数个数和为2，表示对应数组下标的数为质数

1~100之间的质数有25个，分别是

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97

33.(4分)当输入为"1000"时，输出为( C )