信息学奥赛初赛-组合数学-容斥原理应用分析

1 原题

题目描述

有一根60m的绳子，每隔3m做一个记号，每隔4m做一个记号，然后把有记号的地方剪断，问绳子共被剪成了几段？

A. 25 B. 30 C. 35 D. 40

答案 B

分析

60m的绳子，每隔3m做一个记号(绳子的两端不需要剪)，可以做60/3-1=19个

60m的绳子，每隔4m做一个记号(绳子的两端不需要剪)，可以做60/4-1=14个

上面标记19个点和14个点有重合的，这些重合的点既是3的倍数，又是4的倍数，所以这些重合的点是12的倍数

重合点的个数为 60/12-1=4

可以通过容斥原理计算所有的记号

所以标记的点的个数为19+14-4=29个

绳子被剪的段数为标记点的个数+1=29+1=30

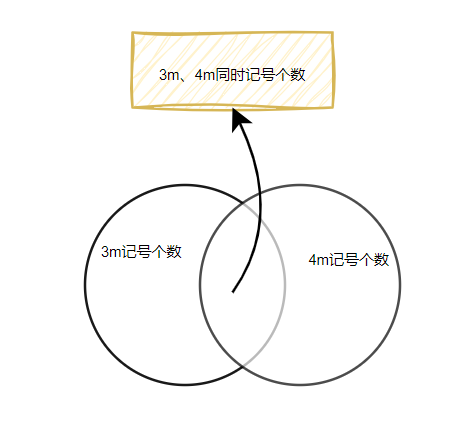
容斥原理 韦恩图 (文氏图) 表示

所有的记号=3m的记号+4m的记号-3m和4m同时标记的记号

2 数据缩小图示-12个数没有重合的点

题目描述

有一根12m的绳子，每隔3m做一个记号，每隔4m做一个记号，然后把有记号的地方剪断，问绳子共被剪成了几段？

分析

每隔3m做一个记号，共12/3-1=3个

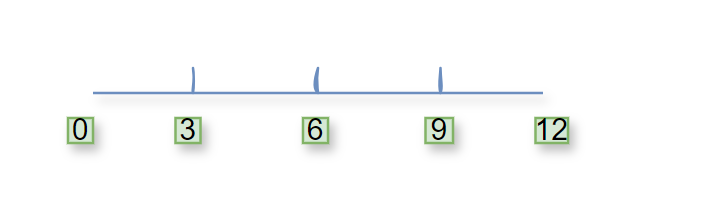
在上面图的基础上，每隔4m再做一个记号，共12/4-1=2个(红色)

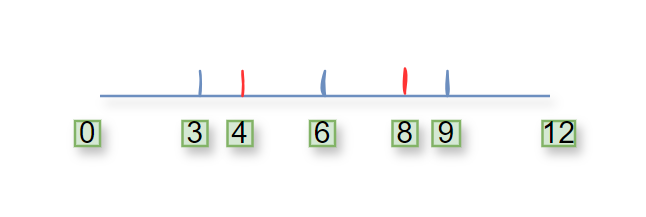
12/3-1=3

12/4-1=2

所以剪的标记为3+2=5个

有图可知，被5个标记点分成了6段

3 数据缩小图示-24个数有重合的点

题目描述

有一根20m的绳子，每隔3m做一个记号，每隔4m做一个记号，然后把有记号的地方剪断，问绳子共被剪成了几段？

分析

每隔3m做一个记号，共24/3-1=7个

在上面图的基础上，每隔4m再做一个记号，共24/4-1=5个(红色)

所以剪的标记为7+5=12个

有图可知，被12个标记点分成了13段