NOIP初赛复习（七）排序与算法复杂度

排序

排序（Sorting）是计算机程序设计中的一种重要操作，其功能是对一个数据元素集合或序列重新排列成一个按数据元素某个项值有序的序列。

简单排序算法

简单排序算法包括冒泡排序、插入排序、选择排序。这三种算法容易理解、编写方便，适用于数据规模较小的情形。

冒泡排序

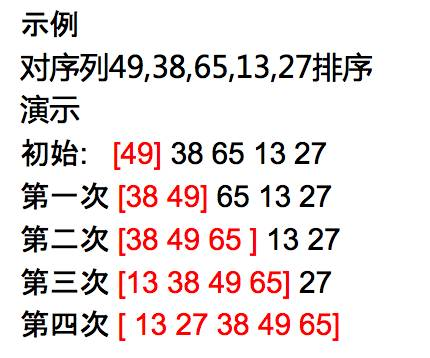
基本思想：两两比较待排序记录的关键字，发现两个记录的次序相反时即进行交换，直到没有反序的记录为止。

排序方法：依次比较相邻的两个数，将大数放在前面，小数放在后面。

 

 

 

 

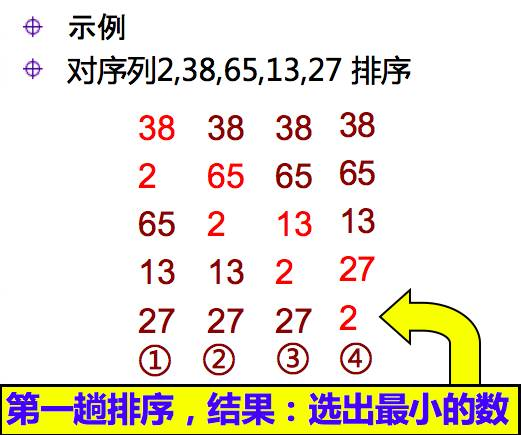
首先比较第1个和第2个数，将大数放前，小数放后。然后比较第2个数和第3个数，将大数放前，小数放后，如此继续，直至比较最后两个数，将大数放前，小数放后，此时第一趟结束，在最后的数必是所有数中的最小数。

 

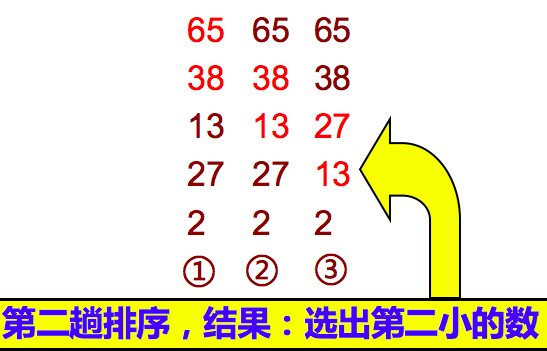
重复以上过程，仍从第一对数开始比较（因为可能由于第2个数和第3个数的交换，使得第1个数不再大于第2个数），将大数放前，小数放后，一直比较到最小数前的一对相邻数，将大数放前，小数放后，第二趟结束，在倒数第二个数中得到一个新的最小数。

 

 

 

 

 

 

 

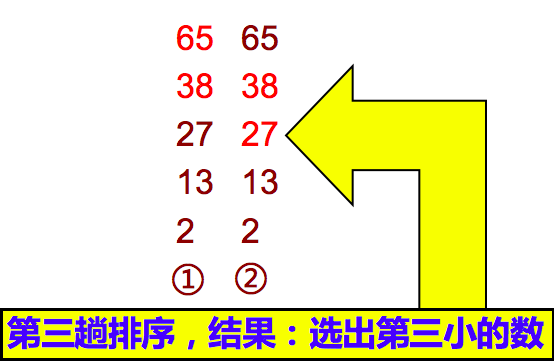
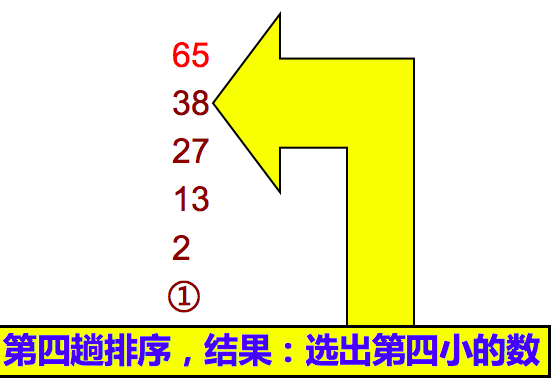
如此下去，直至最终完成排序。

效率分析
空间效率：仅用了一个辅助交换单元。
时间效率：总共要进行n-1趟冒泡，对n个记录的表进行一趟冒泡需要n-1次数值大小比较。

移动次数：最好情况下，待排序列已有序，不需移动。

直接插入排序

基本思想：依次将每个记录插入到一个有序中去。就是说，第i遍整理时，A₁,A₂,...,A_i-1已经是排好序的子序列；取出第i个元素A_i，在已排好序的子序列为A_i找到一个合适的位置，并将它插到该位置上。易知上述排序当i=1时实际上为空操作，故可直接从i=2开始。

排序方法：每步将一个待排序的记录按其关键字的大小插到前面已经排序的序列中的适当位置，直到全部记录插入完毕为止。

 

效率分析

空间效率：仅用了一个辅助单元。
时间效率：向有序表中逐个插入记录的操作，进行了n-1趟，每趟操作分为比较关键码和移动记录，而比较的次数和移动记录的次数取决于待排序列按关键码的初始排列。

对于NOIP提高组而言，这些算法时间复杂度过高，很难应付较大的数据规模。建议尽量不要采用简单排序算法，除非你十分确信数据规模在可承受范围之内。

快速排序

基本思想：基于分治思想。（以从小到大排序为例）取一个数作为标记元素，将比它大的数放在它右侧，比它小的数放在它左侧，再通过递归的方法，将左侧的数用以上的方法排好，右侧的数也用以上的方法排好即可。

在数据规模很大时，平均情况下快排比冒泡快很多。在处理NOIP提高组含排序的问题时，一般要选择快速排序或堆排序。

排序方法：运用分治思想，因而要用函数的递归调用来实现。

 

 

 

 

快速排序实现方法的最差情形是排列整齐的情况，这时它的运行效率会很低。为了解决排列整齐的情形，我们可以使用随机快速排序法，即随机选取一个数作为标记元素（实现时，将其与第一个数交换即可）。

 

---

 

 

 

算法时空复杂度

为了描述一个算法的优劣，我们引入算法时间复杂度和空间复杂度的概念。

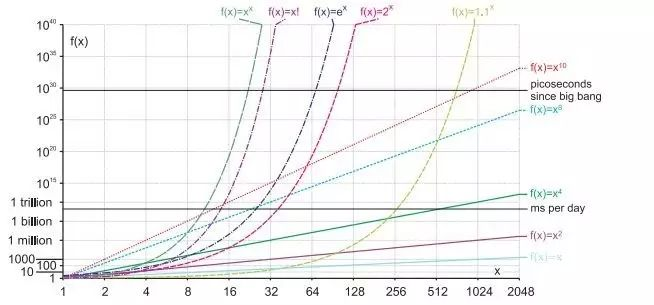
时间复杂度：一个算法主要运算的次数，用 O( )表示。 通常表示时间复杂度时，我们只保留影响最大的项，并忽略该项的系数。

例如主要运算为赋值的算法，赋值做了3n^3+n^2+8次，则认为它的复杂度为 O(n^3)；若主要运算为比较，比较做了4*2^n+2*n^4+700次，由于数据很大时，指数级增长的2^n影响最大，我们认为它的时间复杂度为 O(2^n)。

常见的时间复杂度：

O(n) ——贪心算法多数情况下为此时间复杂度

O(nlbn)——有时带有分治思想的算法的时间复杂度

(注 lbn 表示以2为底的 n 的对数)

O(n^2) ——有时动态规划的时间复杂度

O(n^3) ——有时动态规划的时间复杂度O(2^n) ——有时搜索算法的时间复杂度

O(n!) ——有时搜索算法的时间复杂度

O(m*n)——有时时间复杂度中含有两个或多个字母，比如遍历一个m*n 的矩阵，时间复杂度为 O(m*n)

要注意的是，时间复杂度相同的两个算法，它的实际执行时间可能会有数倍的差距，因而实现时要特别注意细节处的优化。

NOIP 提高组执行时限常常为1s。一般认为，将数据规模代入到时间复杂度，若所得值小于或接近于 1000000，就是绝对安全的、不超时的。

例如：O(n^2)的动态规划算法，可承受的数据规模是 n≤1000；O(2^n)的搜索算法，可承受的数据规模是n≤20；O(n!)的搜索算法，可承受的数据规模是n≤9。实际上，以现在的 CPU 运行速度，5000000也应该不成问题。

空间复杂度：一个算法消耗储存空间(内存)的大小，用 O( )表示。 空间复杂度的表示规则与时间复杂度类似。

在实际应用时，空间的占用是需要特别注意的问题。太大的数组经常是开不出来的，即使开出来了，遍历的时间消耗也是惊人的。

下面我们简单地分析一下简单排序算法、快速排序、堆排序的时空复杂度。这三种算法都是基于比较的排序算法，以比较次数作为主要运算。

时间上，简单排序算法最差时需做 n^2次比较，平均情况下时间复杂度通常被认为是 O(n^2)；快速排序最差时需做 n^2次比较，可以证明平均情况下需做 nlbn 次比较，时间复杂度是 O(nlbn)；堆排序时间复杂度是 O(nlbn)。

空间上，三者都不需要额外开辟暂存数组，快排递归调用时需要使用稍多一些的储存空间。综合来看，快速排序、堆排序优于简单排序算法。另外，可以证明基于比较的排序算法时间复杂度下界为O(nlbn)。

时空的简单优化方法

时间上的优化在于少做运算、做耗时短的运算等。有几个规律需要注意：

1、整型运算耗时远低于实型运算耗时。

2、+、-运算非常快(减法是将减数取补码后与被减数相加，其中位运算更快一些，但是减法也比加法稍慢些。)

3、*运算比加法慢得多/运算比乘法慢得多比较运算慢于四则运算赋值运算慢于比较运算(因为要写内存) 这些规律我们可以从宏观上把握。

事实上，究竟做了几步运算、几次赋值、变量在内存还是缓存等多数由编译器、系统决定。 但是，少做运算（尤其在循环体、递归体中）一定能很大程度节省时间。 下面来举一个例子：

计算组合数 C(m,n)——n 件物品取出 m 件的组合数。 C(m,n)可用公式直接计算。C(m,n)=n!/((n-m)!m!)，C(m,n)=n(n-1)(n-2)...(n-m+1)/(n-m)!。显然，有时所作的乘法少很多，会快一些。

可是这样算真的最快吗？另一条思路是 C(m,n)=C(m,n-1)+C(m-1,n-1)，递推下去，直到可利用 C(1,k)=k=C(k-1,k)为止。这种只用加法的运算会快些，尽管加法多一些。

空间上的优化主要在于减小数组大小、降低数组维数等。常用的节省内存的方法有:

1、压缩储存——例：数组中每个数都只有0、1两种可能，则可以按位储存，空间压缩为原来的八分之一。

2、覆盖旧数据——例：矩阵中每一行的值只与上一行有关，输出只和最末行有关，则可将奇数行储存在第一行，偶数行储存在第二行，降低空间复杂度。

要注意的是，对空间的优化即使不改变复杂度、只是改变 n 的系数也是极有意义的。空间复杂度有时对时间也有影响，要想方设法进行优化。

 

---

 

 

 

计数排序

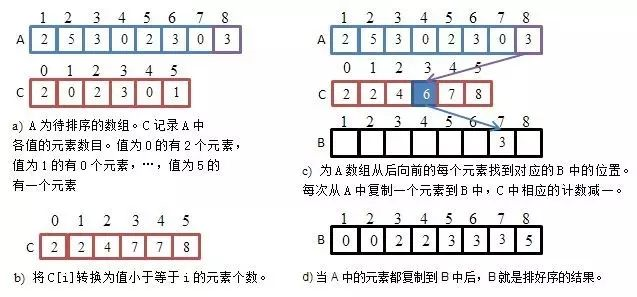
基本思想：开辟暂存数组 b[ ]，b[k]表示欲排序数组 a[ ]中 k 出现的次数（需要遍历a[ ]），最后遍历 b[ ]，可将 a[ ]排好。这种想法非常简单，实现也很容易。

 

 

 

 

事实证明，在 a[ ]取值范围很小（如整型范围）时，它是很高效的排序算法，比快排快不少。可是a[ ]取值范围较大（如长整型范围）时，它的执行时间会变长，而且数组 b[ ]有时开不出来。实际上计数排序时间复杂度为 O(n+m)，空间复杂度也为 O(n+m)，m 表示 a[ ]取值范围。若 m 很大，则也不能在时限内执行完。

归并排序

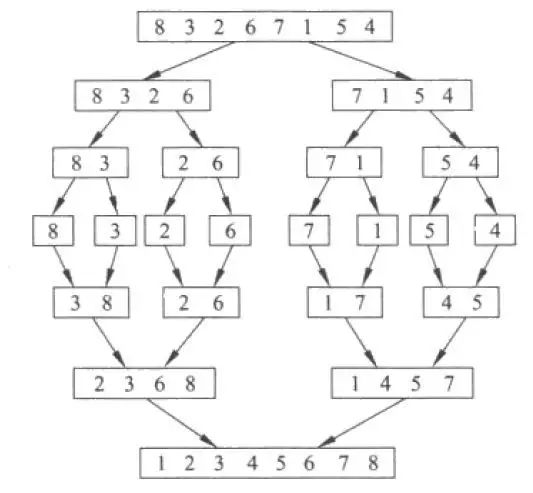
基本思想：将两个或两个以上的有序（大小关系）序列组合成一个新的有序序列。

 

 

 

 

排序方法：

1、将序列每相邻两个数字进行归并操作，形成n / 2个序列，排序后每个序列包含两个元素 。

2、将上述序列再次归并，形成n / 4个序列，每个序列包含四个元素。

3、重复步骤2，直到所有元素排序完毕。

 

 

 

 

 

 

 

排序的稳定性

举例：有一张成绩表，记录着许多学生的成绩，要将他们按成绩排序，但成绩相同者的相对顺序不能改变。换句话说，ABCDE 五人，A、C、D 成绩相同，显然排序完之后会排在一起，现在的要求是：他们排在一起的顺序也必须是ACD，不能是 ADC、CAD...。这样的实际问题涉及到排序的稳定性。

排序的稳定性：一个排序算法，若可使排序前后关键字相同的项相对顺序不变，则称该排序算法是稳定的排序算法。

在编写合理的情况下，简单排序算法是稳定的；快速排序、堆排序是不稳定的。在NOIP中，往往排序是没有附带其他项目的，也就不要求排序稳定。快速排序、堆排序仍然是最佳选择。可是有没有时间复杂度为O(nlbn)的稳定的排序算法呢？有的。归并排序基于分治思想：把要排序的数组平分两半，对两部分分别排序（递归地）后再合并起来。合并时，将一个数组按顺序插入另一个数组中，需要开辟一个暂存数组。利用空间优化，可只用开辟一个与原数组等大的数组。归并排序的优缺点都很明显。无论情形如何，它的比较次数、赋值次数都稳定在nlbn，没有最差情况，运行时间与快速排序、堆排序相当。而且，它是稳定的排序算法。但是，它的内存占用会达到快速排序、堆排序的两倍，竞赛时使用容易造成内存超出限制。

NOIP初赛曾考察过归并排序。问题大意是：找出一个算法，使五个数在n 次比较（两两比较）后一定能排定次序，求n 的最小值。在快速排序、堆排序的最差情况下，需要10次、9次比较。可是，使用归并排序只需要7次！记住：归并排序没有最差情况。

合理选用排序算法

下面是一些主排序算法的优缺点比较：

排序 算法	时间 复杂度	优点	缺点
简单 排序	O(n^2)	编写方便	执行时间长
快速 排序	O(nlbn)	执行时间短	很差情况下执行时间长 占用内存多
堆 排序	O(nlbn)	执行时间短	编写有点麻烦 有较差的情况
计数 排序	O(n+m)	编写方便 取值范围小时很高效	取值范围大时效率低 易超内存限制
归并 排序	O(nlbn)	稳定的排序算法 无较差情况	占用内存很大

竞赛中首选快速排序、堆排序。但有时也应比较各排序的优缺点，依实际合理选用。如：

1. 若n较小(如n≤50)，可采用直接插入或选择排序；
2. 若序列初始状态基本有序（指正序），则应选用直接插人、冒泡或随机的快速排序为宜；
3. 若n较大，则应采用时间复杂度为O(nlbn)的排序方法：归并排序。