CSP初赛复习-28-动态规划

动态规划(Dynamic Programming) 是在20世纪50年代由美国数学家理查德-贝尔曼（Richard Bellman）发明的。

把原问题分解成若干子问题，自底向上求解最小子问题，把子问题的解存储到表格中，然后求解较大问题，求解原问题的解时，需要用到较小子问题的解，可以直接从表格中查询较小子问题的解，避免重复计算，从而提高求解效率

例题 斐波那契数列

如下图

f(3)用到了3次，f(4)用到了2次，在用动态规划解决问题时，f(3)计算1次存储表格，f(4)计算1次存储表格，在使用时直接从表格取，避免重复计算，提高了速度

特别是在求较大斐波那契数时，避免了大量计算，大大提高了算法的响应时间

动态规划解决问题，一般具有如下性质

1 最优子结构

当一个问题的最优解包含着它的子问题的最优解时，称此问题具有最优子结构性质

也可以认为如果对每个子问题的最优解可以构建全局最优解，说明具有最优子结构

斐波那契数列例子中

f(5)=f(4)+f(3) ,f(5)的解可以通过f(4)和f(3)求出，说明具有最优子结构

如果求问题f(5)的解和子问题f(4),f(3)等子问题的解无关，则说明不具有最优子结构

2 重叠子问题

重叠子问题是指求解问题的过程中，每次求解的问题并不是总是新问题，有大量的重复问题存在。

斐波那契数列例子中

f(3)用到了3次，f(4)用到了2次，只计算1次，存储到数组中，后续使用时直接O(1)的时间复杂度直接取出

重叠子问题时动态规划效率高的主要原因

3 无后效性

把原问题分解成若干子问题，每个子问题求解都作为一个阶段，求解当前阶段解时，只与之前已经求出之前阶段的解有关，和之后未求出的阶段无关，这种称作无后效性

由于之前阶段问题的解已经求出，因此无后效性是可以使用动态规划的前提

斐波那契数列例子中

求解f(5)与f(4)和f(3)有关，不与f(5)以后的解有关，说明其具备无后效性

关键连接 -动态转移方程

动态规划解决问题时，把问题分解成一个个小问题，每个问题求解时作为一个阶段。当前阶段和下一个阶段存在着某种联系，这种确定的联系，一定存在着某种方程式(根据前一阶段通过某种关系式计算出下一阶段)，叫做动态转移方程

例题1 爬楼梯 一维动态规划

题目描述

楼梯有 N 阶，上楼可以一步上一阶，也可以一步上二阶

编一个程序，计算共有多少种不同的走法

输入格式

一个数字，楼梯数n (n<40)

输出格式

输出走的方式总数

样例输入

4

样例输出

5

大致思路

1 问题分解每层楼梯的方案数,可以分为n个小问题，即n个阶段

2 dp[i]表示爬到第 i 阶时有多少种方法

3 斐波那契数列模型 第1项目为0 第2项为1 从第3项开始当前项=前2项目之和

4 从小到大，逐项计算出对应的方案数存放入数组中

5 下图列出前10项目爬楼梯的方案数

参考程序

#include <bits/stdc++.h> 
using namespace std;
int n,dp[41]; 
int main(){
    dp[0]=dp[1]=1;//边界 0 1都是1 
    for(int i=2;i<=sizeof(dp)/4;i++){//提前计算前40楼梯方案放入数组中
        dp[i]=dp[i-2]+dp[i-1];//动态转移方程 当前项可以有前2项计算得出
    }
    cin>>n;
    cout<<dp[n];//使用时直接从数组取 
    
}

例题2 - 数字三角形 二维动态规划

题目描述

如下所示为一个数字三角形

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

请编程计算从顶至底部某处的一条路径，使该路径所经过的数字的总和最大

每一步可沿直线向下或右斜线向下走

输入格式

第一行为一个自然数，表示数字三角形的行数 n
接下来的 n 行，表示一个数字三角形。同一行的两数之间都有一个空格

输出格式

输出一行一个整数，表示要求的最大总和

样例输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出

30

大致思路

1 把求解走过的路径数字和最大值，分解为求走过路径每个点的数字最大值，由于不知道具体走哪条路径最大，因此需要先把二维数组所有点

2 求出走到二维数组dp[i] [j] 所有数字和的最大值，提前计算出来存入二维表格

3 计算当前dp[i] [j] 数字和最大值，由于只能从左上和正上走来，所以dp[i] [j] 之和左上dp[i-1] [j-1]

正上dp[i-1] [j] 有关，即左上和正上取较大的 再加上自己

4 状态转移方程 dp[i] [j]=max(dp[i-1] [j-1],dp[i-1] [j])+a[i] [j]

5 最优子结构 走到某一位置的数字和最大值可以由前面子问题最大和计算出，因此具有最优子结构性质

6 重叠子问题 计算出来的数字和会再计算后续更大问题时被多次计算，因此具有重叠子问题，可以减少重复计算

7 无后效性 计算走到某一位置最大值时，只和前面左上和正上的子问题相关，后面未走过的位置无关，因此具有无后效性的性质

具体数据参考

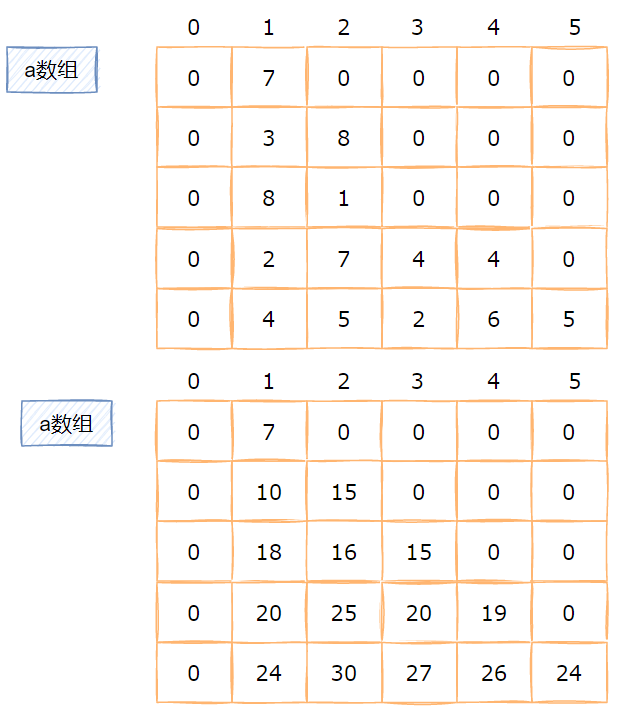
参考程序

#include<bits/stdc++.h>
using namespace std;
//ans 保存最大数 a[i][j]读取三角形对应数字 
int ans,a[105][105],dp[105][105];//dp[i][j]走到i行j列时的数字和最大值 
int main(){
    int n;
    cin>>n;//录入行数 
    for(int i=1;i<= n;i++){
    	for(int j=1;j<=i;j++){//j<=i三角形列最大到行数 
    		cin>>a[i][j];//输入数字三角形对应数字 
		}
	}
             
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            //走过路径最大数字和为左上和正上最大值+当前值 
            dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j];
        }
    } 
         
    for(int j=1;j<=n;j++){//最大值必然在最后一行  
        //在最后一行，取最大数
        ans = max(ans,dp[n][j]);
    } 
    cout<<ans<<endl;
    return 0;
}

CSP初赛复习-28-动态规划-练习题
https://www.cnblogs.com/myeln/articles/17626730.html