CSP初赛复习-16排序-进阶

计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，并且考虑到存储空间的限制计数排序要求输入的数据必须是有确定范围的整数

计数排序对数据的要求十分严格：

1 计数排序适用于数据范围不大且小于元素个数的情况；

2 待排序数据的最小单位需为整数，如果不是，需转换到整数，排序后恢复；

3 待排序数据需为正，如果不是，则需转化为非负，排序后恢复

排序过程

1 找出原始数组L中最大的元素值max

2 构造一个计数数组count，count的下标为从0到max，下标为待排序数字

3 从前往后遍历计数数字，如果计数数字某个元素为多个，则多个逐个输出

示例图

对 5 4 8 9 7 进行排序

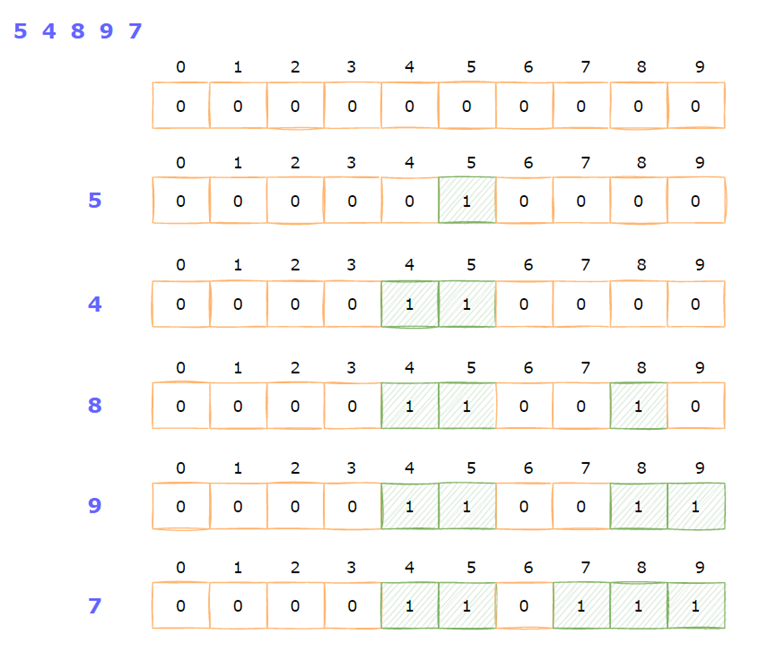
计数排序动图

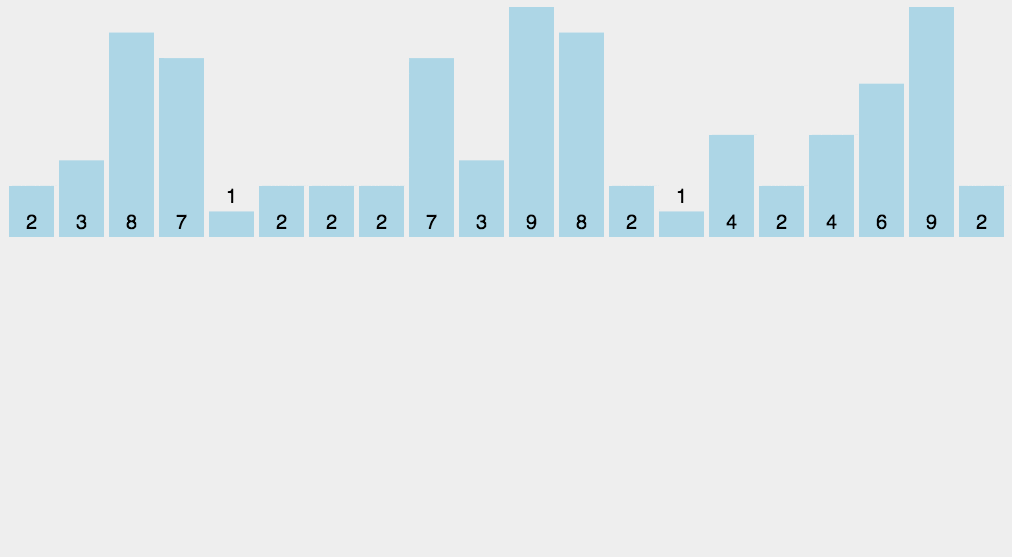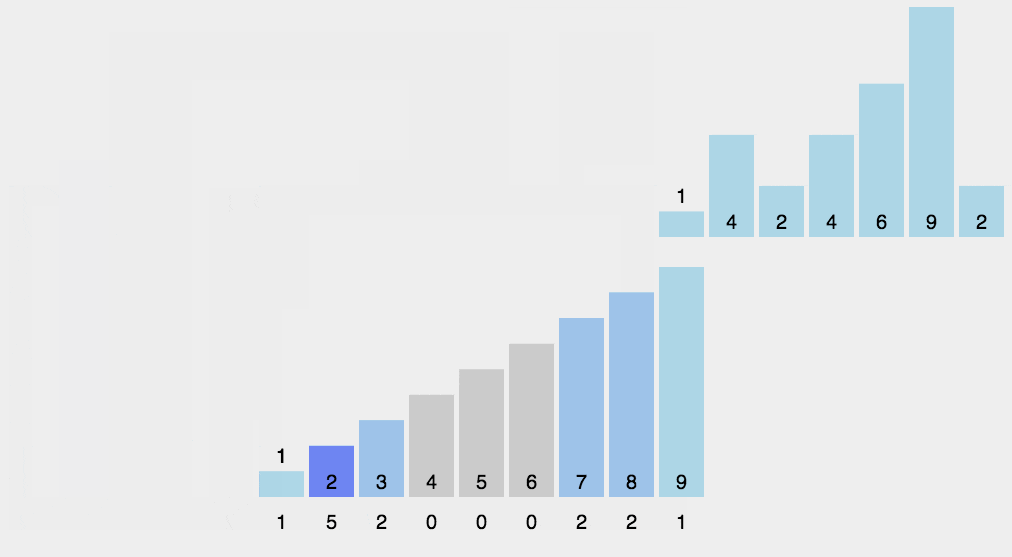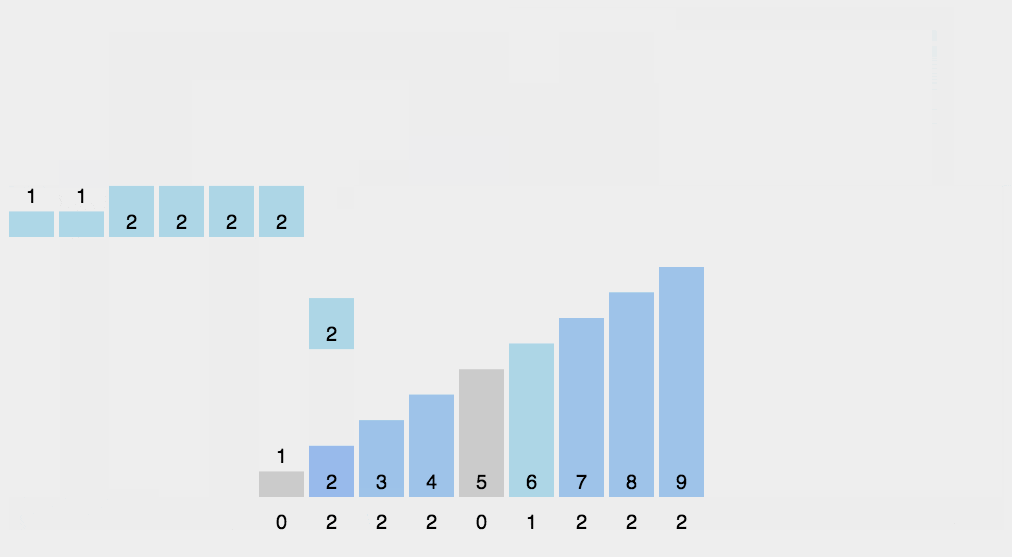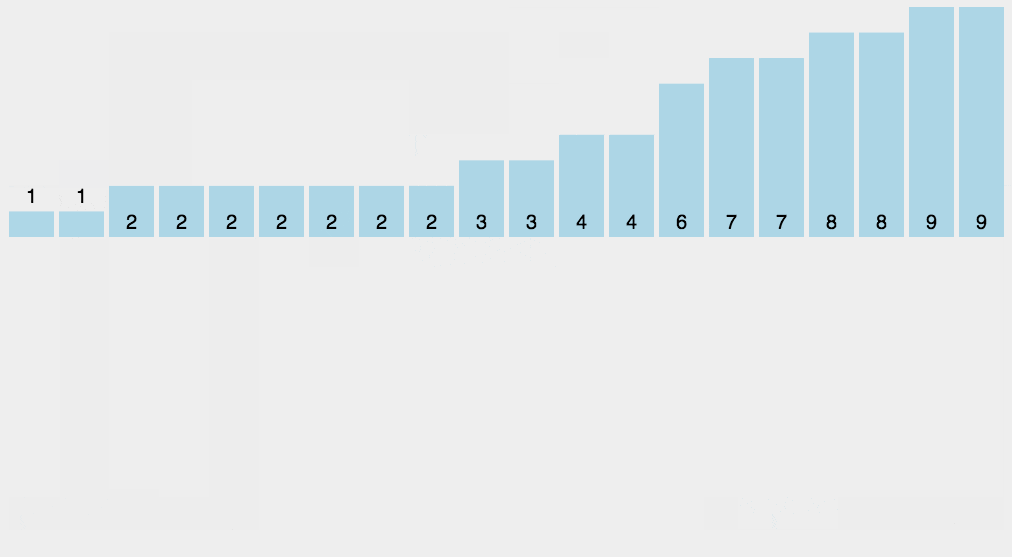
示例程序

#include<bits/stdc++.h>
using namespace std;

void show(int a[],int length){
    for(int i=1;i<=length;i++)
        cout<<a[i]<<' ';
}
/*
计数排序
100 93 79 71 65 55 53 21 9 42
temp[9]=1
temp[21]=1
temp[42]=1
temp[53]=1
temp[55]=1
temp[65]=1
temp[71]=1
temp[79]=1
temp[93]=1
temp[100]=1
其他temp为0 
*/ 
void countingSort(int a[],int length){
    int temp[101]={0};
    for(int i=1;i<=length;i++){
        temp[a[i]]++;//把a[i]作为下标 值累加进temp数字 
    }
    int k=1;
    for(int i=1;i<=100;i++){// 1-100循环遍历 temp[i]的值 9 23 42 ... 
        for(int j=0;j<temp[i];j++){//此数出现过几次temp[i]为几 0-8都无法进入循环 
            a[k++]=i;//按排序复原a数组 a[1]=9 a[2]=23 a[3]=42
        }
    }
}

int main(){
    int a[11]={0, 100, 93, 79, 71, 65, 55, 53, 21, 9,42};
    int n=10;
    /*
    for(int i=1;i<=10;i++)
        cin>>a[i];
    */
    countingSort(a,n);
    
    show(a,n);
    return 0;
}

时间复杂度

平均时间复杂度

O(n+k) 其中n待排序数字长度，k为计数数组长度

最好时间复杂度

O(n+k) 其中n待排序数字长度，k为计数数组长度

最坏时间复杂度
O(n+k) 其中n待排序数字长度，k为计数数组长度

稳定性

稳定

排序后 2 个相等键值的顺序和排序之前它们的顺序相同

快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快

快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法

1 从数列中挑出一个元素，称为 “基准”

2 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。

3递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

1 对如下5个数字进行快速排序

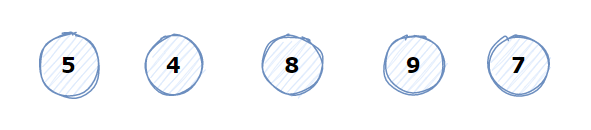
2 找最左边点为基准点

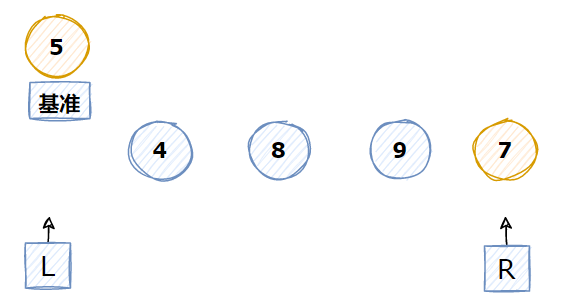
3 基准点5<右边点数字7 所以不需要移动，指针R左移

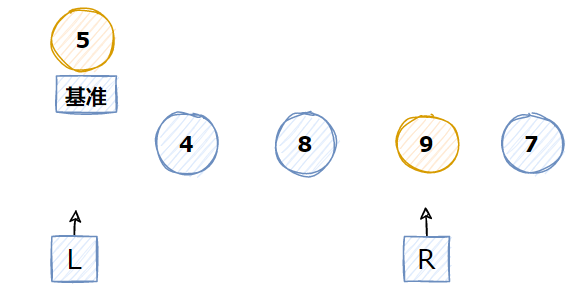
4 基准点5<右边点数字9 所以不需要移动，指针R左移

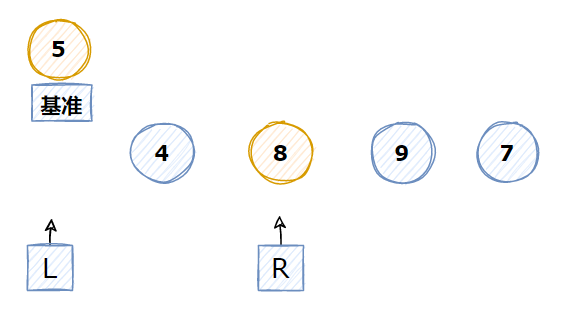
5 基准点5>右边点数字4 ,所以4左移，指针L右移

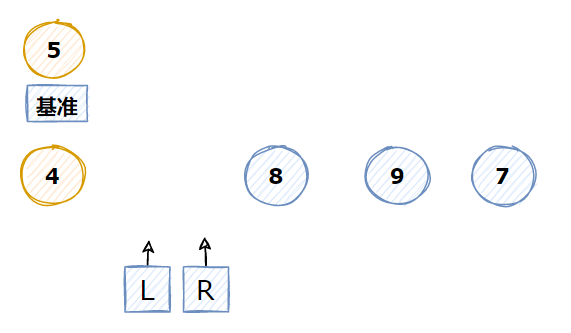
6 一轮结束，通过基准点分成两部分，左边比基准点小，右边比基准点大

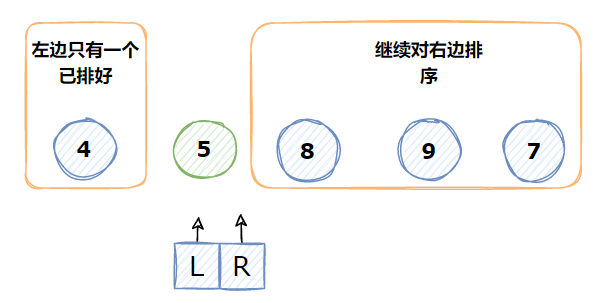
7 左边只剩一个元素，已经排好序，需要对右边进行上述一轮操作

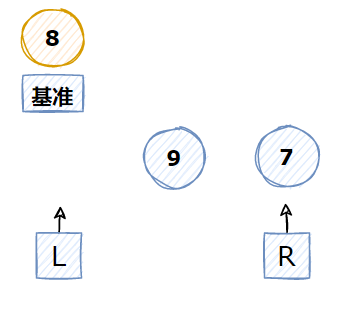
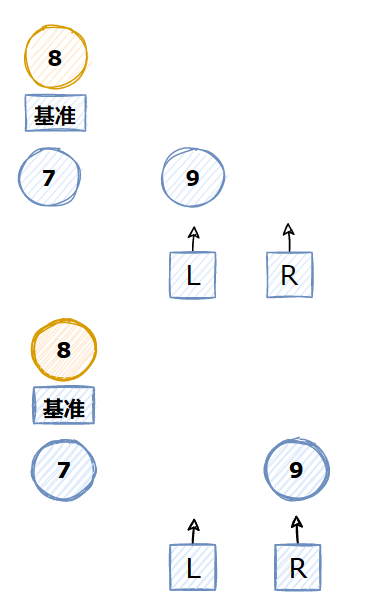
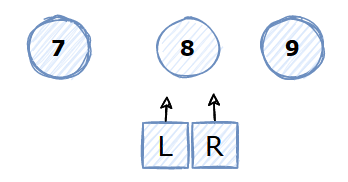
快速排序动图

示例代码

#include<bits/stdc++.h>
using namespace std;
void quickSort(int arr[],int l,int r){
    int i=l,j=r,mid=arr[l];
//    mid=arr[l+rand()%(r-l+1)];
    while(i<=j){
        while(arr[i]<mid) i++;
        while(arr[j]>mid) j--;
        if(i<=j){
            swap(arr[i],arr[j]);
            i++;
            j--;
        }
    }
    if(l<j) quickSort(arr,l,j);
    if(i<r) quickSort(arr,i,r);
}

int main(){
    int a[100],n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    quickSort(a,0,n-1);
    for(int i=0;i<n;i++){
        printf("%d ",a[i]);
    }
}
/*
输入: 
5
5 4 3 2 1
输出:
1 2 3 4 5
*/

时间复杂度

平均时间复杂度

O(n * logn)

最好时间复杂度

O(n * logn)

最坏时间复杂度
O(n^2)

稳定性

不稳定

排序后 2 个相等键值的顺序和排序之前它们的顺序可能不相同

归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。

该算法是采用分治法（Divide and Conquer）的一个非常典型的应用

归并排序是一个基于分治法思想的算法，主要分两步骤完成

1把整个序列平均分成两部分，得到的子序列继续平分下去

2 一直拆分下去，直到拆分的每一部分都只有一个元素为止

3 从底层开始重新组合成一个有序的序列，指定所有元素都被合并

1 排序过程

中间拆分过程

2 合并过程

每次合并两部分，并且通过一个临时数组分别取每个数组最小的，完成2部分排序

归并排序动图

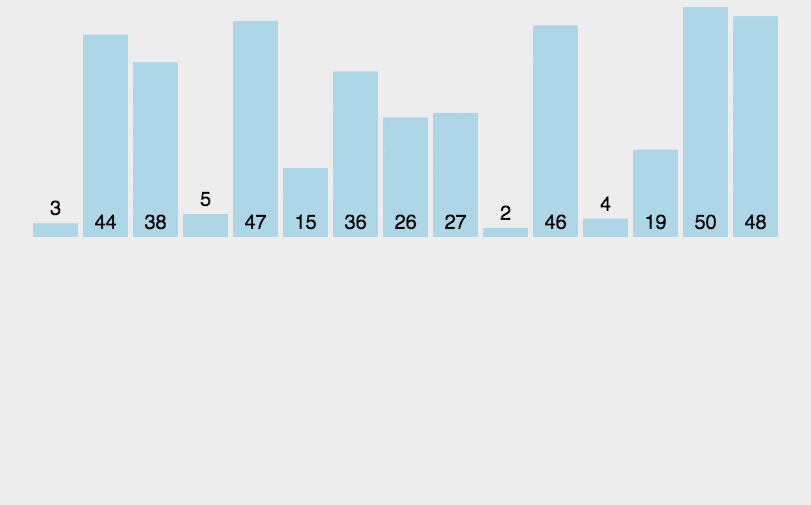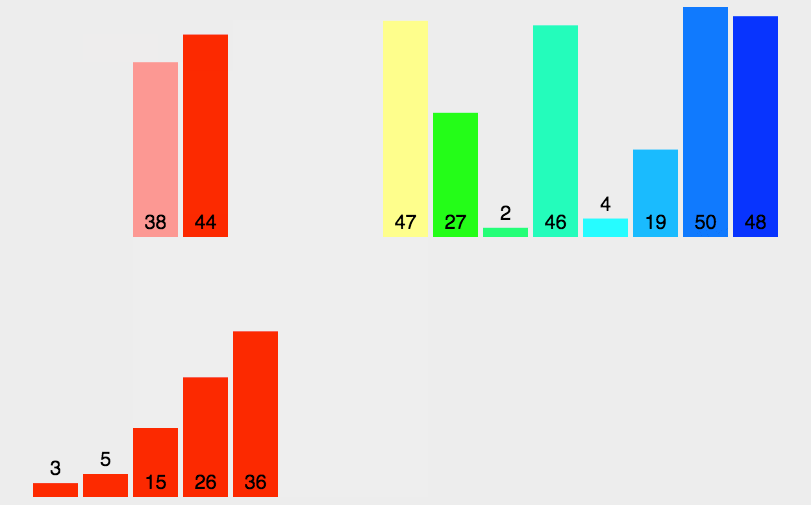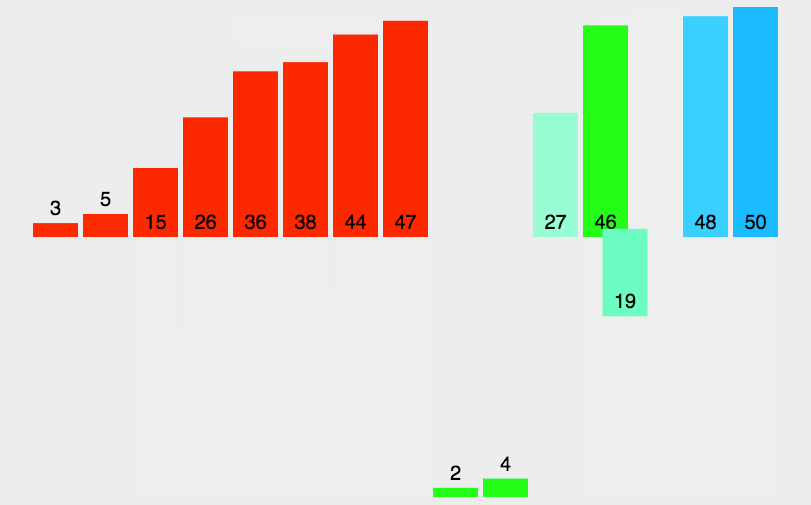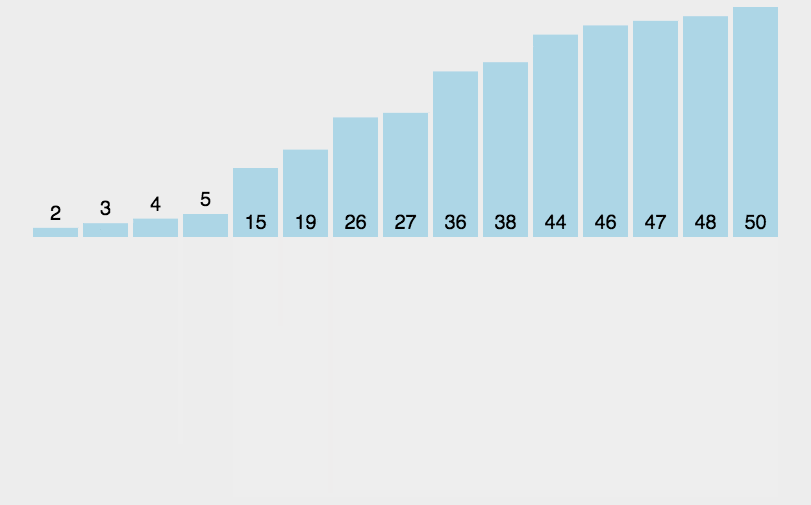
时间复杂度

平均时间复杂度

O(n * logn)

最好时间复杂度

O(n * logn)

最坏时间复杂度
On * logn)

稳定性

稳定

排序后 2 个相等键值的顺序和排序之前它们的顺序相同

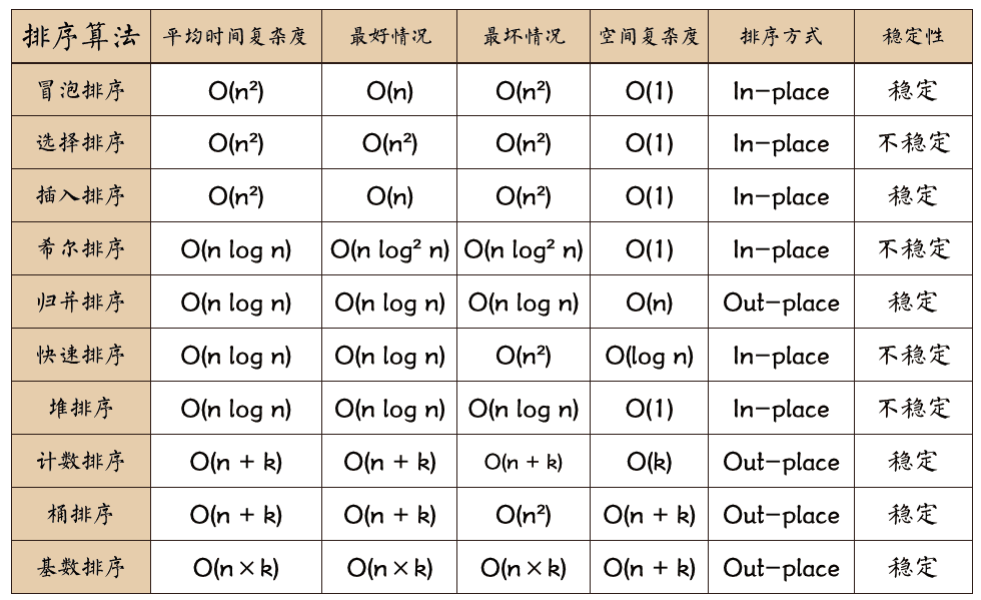
除了上述介绍的6种基本排序算法，还有希尔排序/堆排序/桶排序/基数排序，这些排序算法也可能出现在阅读程序或者补充程序种

程序的时间复杂度，往往考察的可能不是平均时间复杂度，更多是最坏时间复杂度或者最好时间复杂度

排序的稳定性 ，往往也是考察内容之一

因此下表需要熟练掌握

CSP初赛复习-16-数据结构-排序-练习题
https://www.cnblogs.com/myeln/articles/17574468.html