电子学会五级-分治时间复杂度-主定理
主定理是分治算法分析中非常重要的定理
如,我们要处理一个 规模为 n 的问题通过分治,得到 a 个规模为 \(\frac{n}{b}\) 的问题,分解子问题和合并子问题的时间是 f(n):
$ T(n) = aT(\frac{n}{b})+f(n)$
在上面这个式子里,我们得要求 \(a \geqslant 1, b> 1\) (如果 b=1 时,递推无意义),f(n) 是渐进意义上的正数。
回顾一下,a 和 b 的含义:
a 个子问题,即 a 是原问题分为子问题的个数;
每个子问题的规模是 \(\frac{n}{b}\);
分治算法共三部分,分治合,而 f(n) 就是分+合的时间
若 \(T(n)=a*T(\frac{n}{b}) + O(n^d)\) 对于a>0,b>1,d>=0
则有
应用距离
1.二分查找(Binary search):
T(n)=T(n/2)+1
a=1 b=2
因为
\(1=n^0 且 n^{log_{2}{1}}=n^0\)
所以适合情况2 时间复杂度为
\(n^d*log_{2}{n}=log_{2}{n}\)
2.归并排序(Merge sort):
T(n)=2T(n/2)+n
a=2 b=2
\(log_{2}{2}=1 且~~ f(n)=n=n^1\)
所以适合情况2 时间复杂度为
\(n*log_{2}{n}\)
3.二叉树遍历(Binary tree traversal):
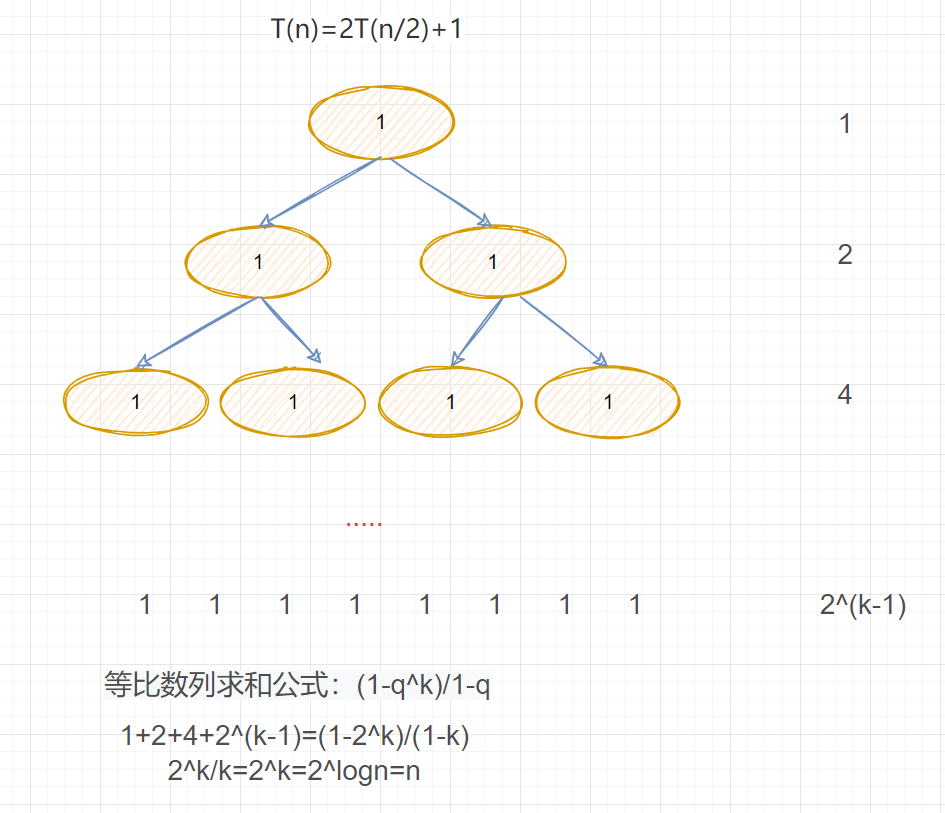
T(n)=2T(n/2)+1
a=2 b=2
\(log_{2}{2}=1 且~~ f(n)=1=n^0\)
所以适合情况3 时间复杂度为
\(n^{log_{b}{a}} = n^{log_{2}{2}}=n\)
4.T(n)=3T(n/4)+nlogn
a=3 b=4
\(log_{4}{3}<1 且~~ f(n)=n^1*logn\)
所以适合情况3 主要看f(n)的时间复杂度
所以时间复杂度为nlogn
https://blog.csdn.net/qq_41739364/article/details/101224786
https://blog.csdn.net/qq_37375427/article/details/100865396
https://blog.csdn.net/weixin_43560913/article/details/119616265
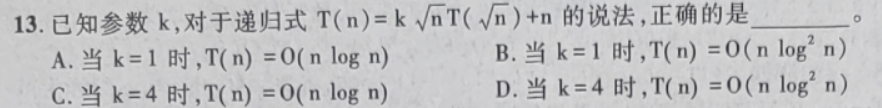
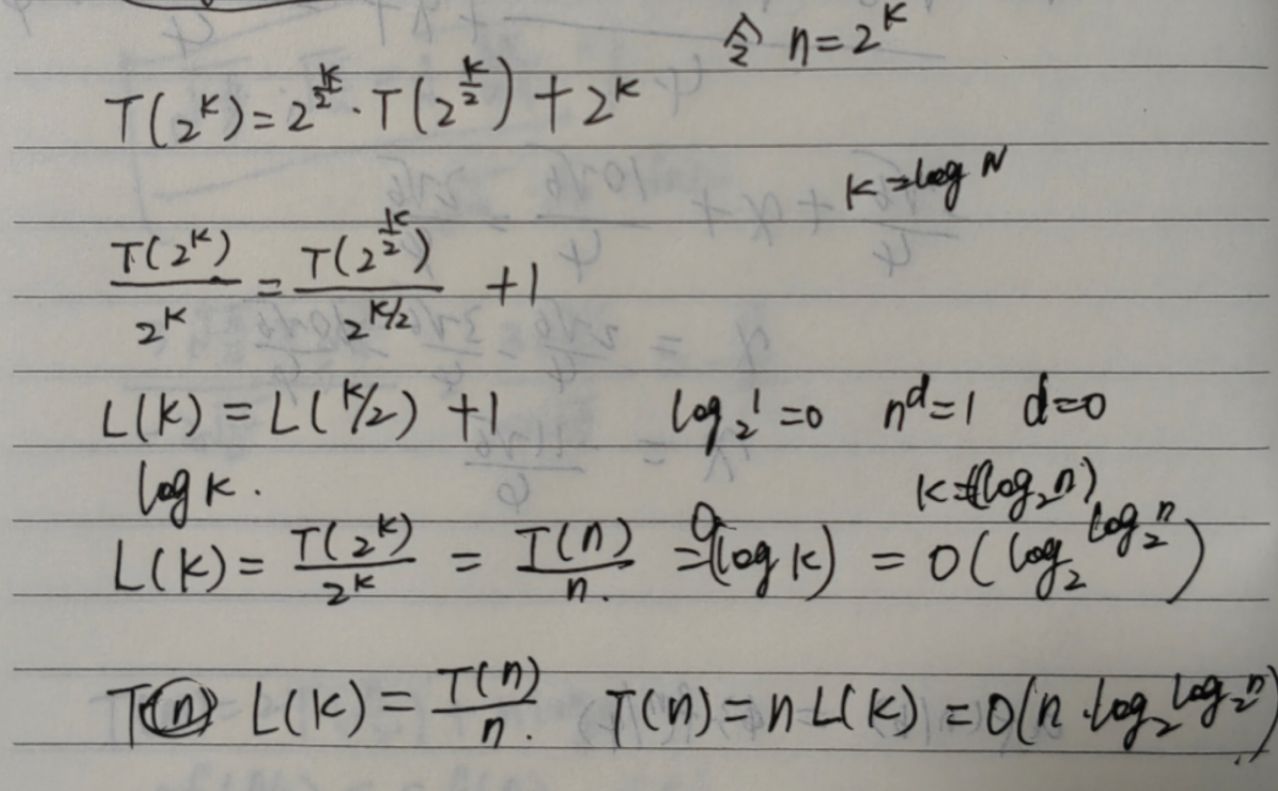
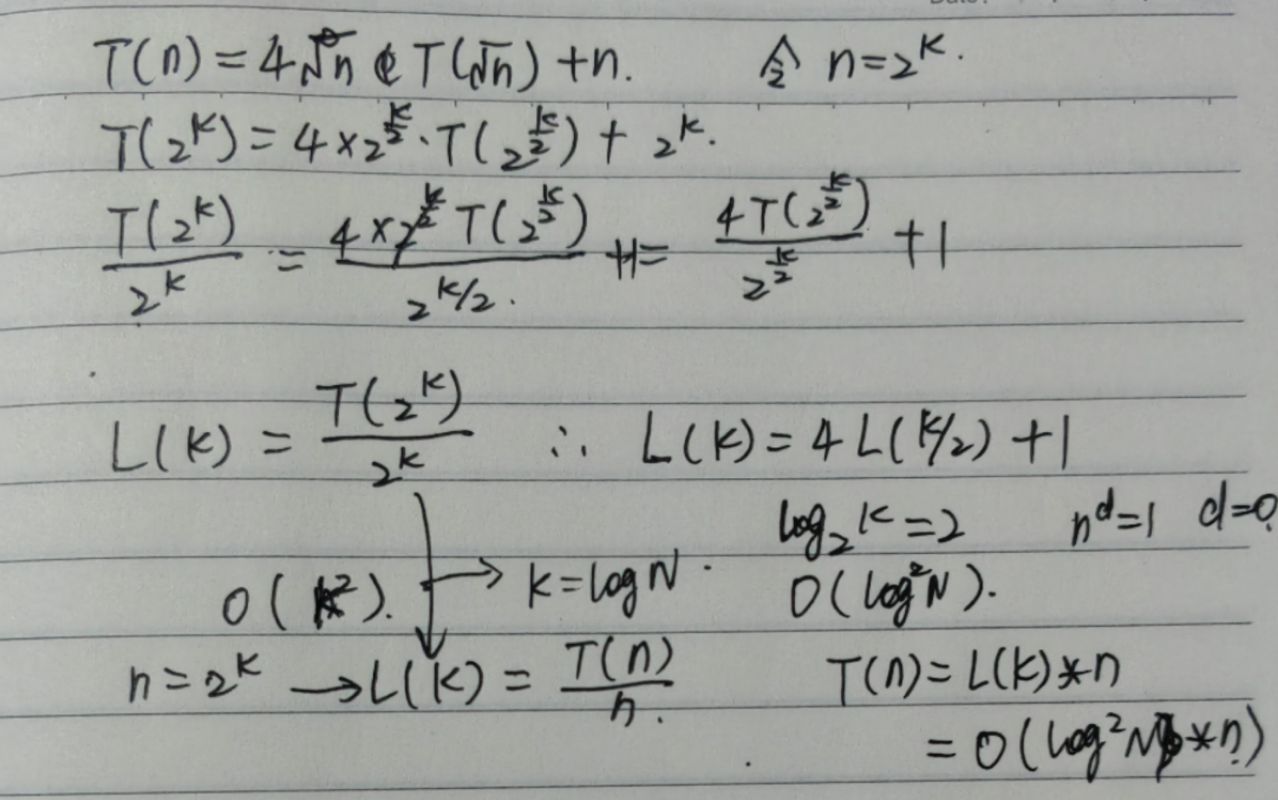
不适用主定理情况
n不等比例缩小 而是逐渐缩小
1.T(n)=T(n-1)+n 时间复杂度 \(O(n^2)\)
推导:
T(n)
=T(n-1)+n
=T(n-2)+(n-1)+n
=T(n-3)+(n-2)+(n-1)+n
…
=T(0)+1+2+…+(n-2)+(n-1)+n
=1+1+2+…+(n-2)+(n-1)+n
=1+(n+1)*n/2
2.T(n)=T(n-1)+1/n 时间复杂度 \(O(logn)\)
推导:
T(n) = T(n-1)+1/n
= T(n-2)+1/(n-1)+ 1/n
= T(n-3)+1/(n-2) +1/(n-1)+ 1/n
……
= T(2)+1+1/2+… +1/(n-1)+ 1/n
= 1+1+1/2+… +1/(n-1)+ 1/n
=O(logn)
当n趋于无穷大时调和级数有:(1 + 1/2 + 1/ 3 + 1/ 4.) - lnn
所以时间复杂度为对数级
- T(n)=T(n/2) + n
不满足 af(n/b)<=cf(n)
f(n/2)=n/2=n<=cn --n/2到n放大,c不可能小于1
可以使用代入法计算 T(n)=n+n/2+n/4+n/8+...1
根据等比数列求和:
\(S(n)=a1*(1-q^n)/(1-q)=1*(1-2^{log^n})/(1-2)=2^{log^n}-1=2^{log^n}=n\)
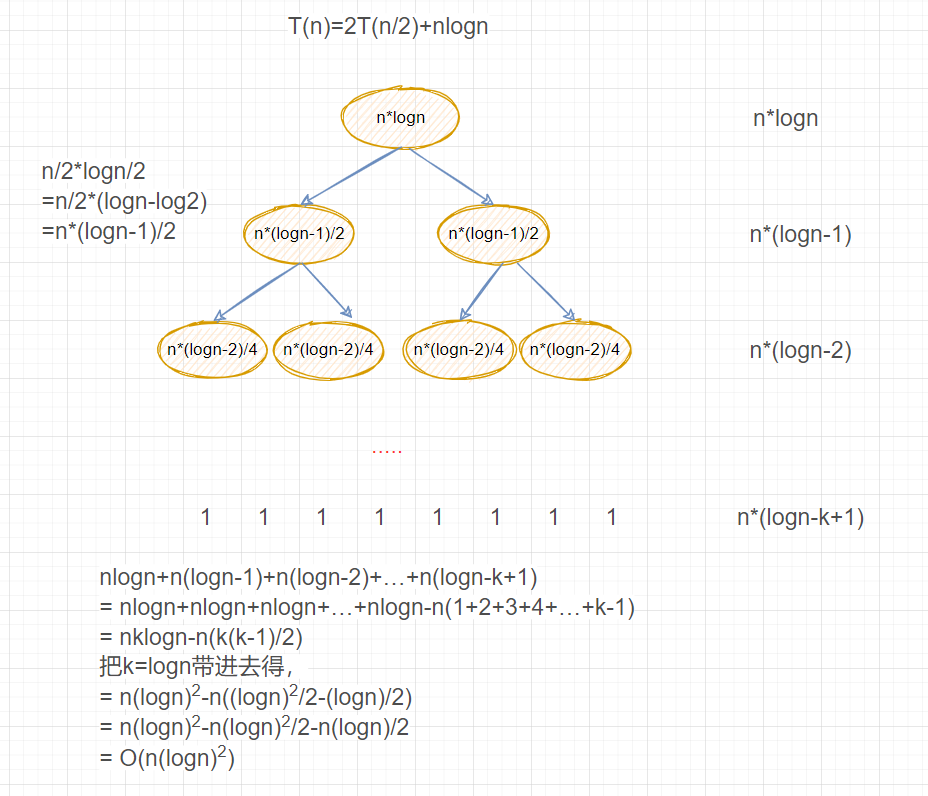
4.T(n)=2T(n/2)+n*logn
a=2 b=2
\(log_{2}{2}=1 且~~ f(n)=n^1*logn\)
不满足 af(n/b)<=cf(n)
\(2*(n/2 * log^{n/2})=n*log^{n/2}=n*log^n <=c*n*log^n ~所以c=1 不满足c<1\)
所以2T(n/2)和nlogn多项式属于同阶
所以T(n)的时间复杂度为:每层规模nlogn再乘以递归深度logn
所以T(n)的时间复杂度为:nlognlogn
https://www.zhihu.com/question/63075755
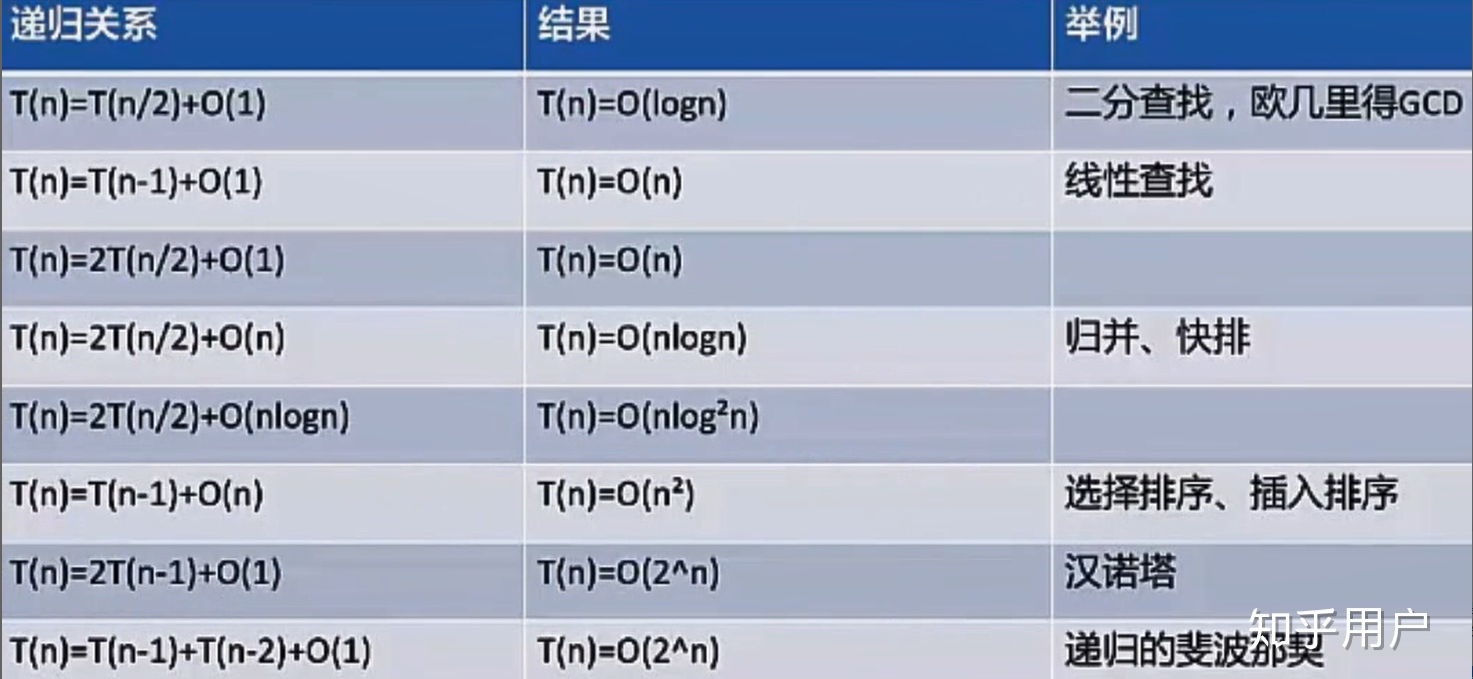
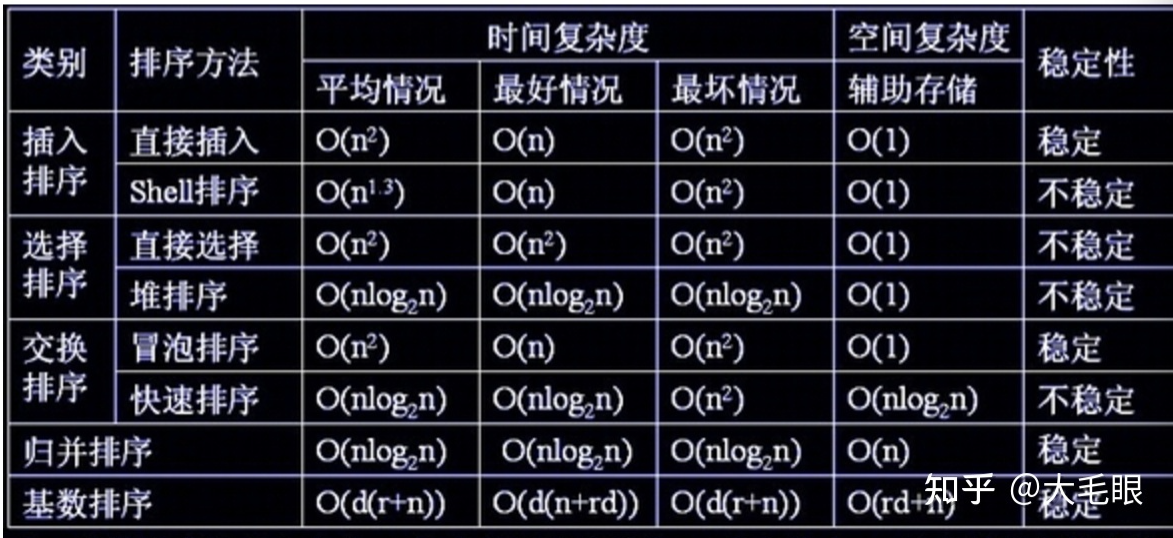
主定理参考
https://blog.csdn.net/weixin_47268276/article/details/109706486
作者:newcode 更多资源请关注纽扣编程微信公众号

从事机器人比赛、机器人等级考试、少儿scratch编程、信息学奥赛等研究学习


 浙公网安备 33010602011771号
浙公网安备 33010602011771号