电子学会八级-基础算法-位运算

位运算那些事儿
https://www.bilibili.com/video/BV1u3411m7fg?spm_id_from=333.337.search-card.all.click
带你读《算法竞赛进阶指南》
https://www.bilibili.com/video/BV1334y1178n?spm_id_from=333.337.search-card.all.click

运算符优先级

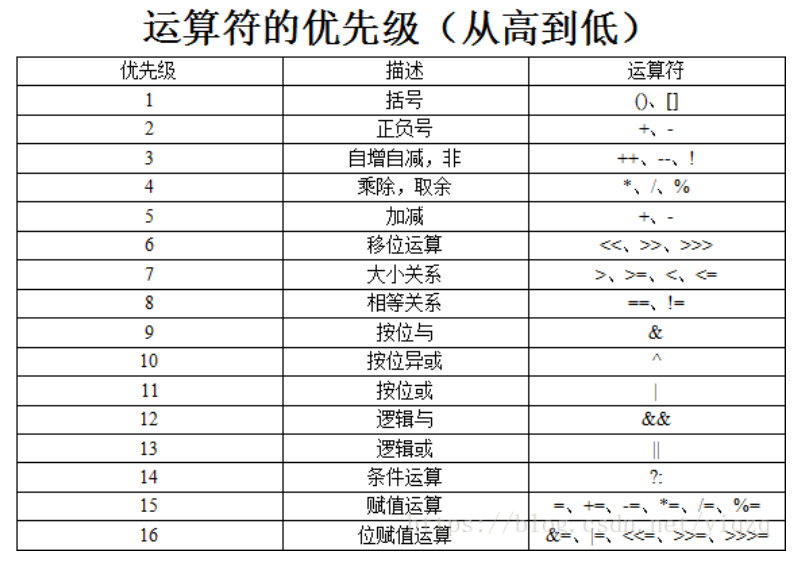
位运算符优先级

  /*
按位取反     >     左移 右移     >      按位与     >    异或      >     或
   ~        >      <<   >>     >        &        >     ^       >      |
  */

常用运算符优先级

  /*
      按位取反   >   乘 除 取余  加 减   >     左移 右移     >   相等关系    >   按位与     >    异或      >     或
         ~      >    *  /  %    +  -   >      <<   >>     >    ==  !=     >     &       >      ^       >     |
  */

#include<bits/stdc++.h>
using namespace std;
/*
取整数 n 在二进制表示下的第k位 (n>>k)&1  				--test1 
取整数 n 在二进制表示下的 0~k-1位 --后k位  n&((1<<k)-1) --test2 
把整数 n 在二进制表示下的第k位取反 n xor(1<<k) 			--test3 
对整数 n 在二进制表示下的第k位赋值 1 n|(1<<k) 			--test4 
对整数 n 在二进制表示下的第k位赋值 0 n&(~(1<<k)) 		--test5 
	
置位 set bit    --  n|=1<<k 						--同test4 
清位 clear bit  --  n&=~(1<<k) 						--同test5 
	
第k位 0还是1 1返回true 0返回false
测位 test bit   --  (n&1<<k)!=0 					--test6
	                    (n>>k&1)!=0					--test7
						
取最后一个非0位   -- A & -A							--test8
	                  -- A & ~(A-1)					--test9
统计非0位         -- for(;A;A-=A & -A) ++cnt        --test10

					  
判断是否相邻的1   -- (A & A>>1) ==0                 --test11
交换两个整数      -- a^=b,b^=a,a^=b 				--test12 
	
检查某个数是否是2的幂
if(n&n-1==0) 如果true则表示为2的n次方				--test13
	
计算n中1的个数										--test14
int n，count=0;
while(n){
	  count+=n&1；
	  n=>>1;
}
*/

/*
	取整数 n 在二进制表示下的第k位 (n>>k)&1
*/
void test1(){
	int n=10,k=2;//1010 --1010>>2 -->10 & 1 = 0
	int ret=(n>>k)&1;
	cout<<ret<<endl;
	k=3;// --1010>>3 -->1 & 1 = 1 
	ret=(n>>k)&1;
	cout<<ret<<endl;
}

/*
	取整数 n 在二进制表示下的 0~k-1位 --后k位  n&((1<<k)-1)
*/ 
void test2(){
	
	int n=10,k=2;//1010 --1<<2 -->100 - 1 =011 -->1010 & 0011 =10 =2
	int ret=n&((1<<k)-1);
	cout<<ret<<endl;
	k=3;// --1010 --1<<3 -->1000 - 1 =0111 -->1010 & 0111 =010 =2
	ret=n&((1<<k)-1);
	cout<<ret<<endl;
}

/*
	把整数 n 在二进制表示下的第k位取反 n xor(1<<k) 
*/ 
void test3(){
	
	int n=10,k=2;//1010 --第k位 从右到左 0 1 2  2位取反 变成 1110=14 
	int ret=n xor(1<<k); 
	cout<<ret<<endl;
}

/*
	对整数 n 在二进制表示下的第k位赋值 1 n|(1<<k)
*/ 
void test4(){
	
	int n=10,k=2;//1010 --第k位 从右到左 0 1 2  2位赋值1 变成 1110=14 
	int ret=n xor(1<<k); 
	cout<<ret<<endl;
}

/*
	对整数 n 在二进制表示下的第k位赋值 0 n&(~(1<<k))
*/ 
void test5(){
	int n=10,k=2;//1010 --1<<2 =100  ~100 =1011  1010&1011=1010 =10
	int ret=n&(~(1<<k)); 
	cout<<ret<<endl;
}

/*
	测位1 test bit 第k位 0还是1 1返回true 0返回false
*/ 
void test6(){
	int n=110,k=2; 
	// 1<<2 ==100 --110 &100 =100 =2  不等0 根据逻辑表达式非0为1 ==非false为true 
	if((n&1<<k)!=0){
		cout<<"k==1"<<endl;
	}else{
		cout<<"k==0"<<endl;
	}
	
	n=1010,k=2; 
	// 1<<2 ==100 --1010 &0100 =0  等0 根据逻辑表达式非0为1 ==非false为true 
	if((n&1<<k)!=0){
		cout<<"k==1"<<endl;
	}else{
		cout<<"k==0"<<endl;
	}
}

/*
	测位2 test bit 第k位 0还是1 1返回true 0返回false
*/ 
void test7(){
	int n=110,k=2; 
	// 110>>2 --1 & 1 =1  不等0 根据逻辑表达式非0为1 ==非false为true 
	if((n>>k&1)!=0){
		cout<<"k==1"<<endl;
	}else{
		cout<<"k==0"<<endl;
	}
	
	n=1010,k=2; 
	// 1010>>2 --10 & 1 等0 根据逻辑表达式非0为1 ==非false为true 
	if((n>>k&1)!=0){
		cout<<"k==1"<<endl;
	}else{
		cout<<"k==0"<<endl;
	}
}

/*
	lowbit 取最后一个非0位
	A & -A --    8      &     -8
	原码      00001000  &     10001000
	反码      00001000  &     11110111
	补码      00001000  &     11111000 = 1000 = 8 
*/
void test8(){
	int A=8; 
	int ret = A & -A;
	cout<<ret<<endl;
}

/*
	lowbit 取最后一个非0位
	A = 8 
	  A           (A-1)			~(A-1)		A  &  ~(A-1)
		      	00001000       00000111	      11111000    
	~(A-1)      11111000
	A&~(A-1)    00001000 =8     
*/
void test9(){
	int A=8; 
	int ret = A & ~(A-1);
	cout<<ret<<endl;
}

/*
	for(;A;A-=A & -A) ++cnt;
	统计十进制对应二进制1的个数 
	logbit： A & -A 取最后一个1对应二进制  比如：110 --10 
	10 -- 110 --第一次循环 110-10=100 第二次循环 100-100=0
	A为0 for循环表达式为false 退出循环 
*/
void test10(){
	int A=10,cnt=0;
	for(;A;A-=A & -A) ++cnt;
	cout<<cnt;
}

/*
	判断是否右相邻的1 
	(A & A>>1) ==0 
	A		10101  
	A>>1 	01010
			0
	
	A		11110
	A>>1	01111
			01110
*/
void test11(){
	int A=10; //--1010
	if((A & A>>1) ==0){//没有相邻的1 
		cout<<"没有相邻的1"<<endl; 
	}else{//有相邻的1 
		cout<<"有相邻的1"<<endl;
	} 
	
	A=11; //--1011
	if((A & A>>1) ==0){//没有相邻的1 
		cout<<"没有相邻的1"<<endl; 
	}else{//有相邻的1 
		cout<<"有相邻的1"<<endl;
	} 
}

/*
	交换两个整数
	-- a^=b,b^=a,a^=b
	a=8 b=7
	 1000
   ^ 0111
     1111
	 
	 a=1111 b=0111
	1111
  ^ 0111
    1000
	a=1111 b=1000
	1111
  ^	1000
	0111 
	a=0111 b=1000  a=7  b=8	
*/
void test12(){
	int a=8,b=7;
	cout<<"a="<<a<<",b="<<b<<endl;
	a^=b;
	b^=a;
	a^=b;
	cout<<"a="<<a<<",b="<<b<<endl;
}

/*
	检查某个数是否是2的幂
	if(n&n-1==0) 如果true则表示为2的n次方
	
	n=2^3=8      n-1=7
		1000 	    0111
	  1000
	^ 0111
	  0000   =0
	运算符优先级  * / % > + - >  & > ==
*/
void test13(){
	int n=8;
	
	if((n&n-1)==0){
		cout<<"n是2的幂";
	}else{
		cout<<"n不是2的幂";
	}
}

/*
	计算n中1的个数
	int n,count=0;
	while(n){
		count+=n&1;//取最右测一个1 
		n=>>1;//右移一位 右侧第2位变为第1位 继续循环取最右测1 
	}
	
*/
void test14(){
	int n=10,count=0;
	int nn=n;
	while(n){
		count+=n&1; 
		n>>=1; 
	}
	cout<<nn<<"包含"<<count<<"个1"<<endl;
	
	n=14,nn=n,count=0;
	while(n){
		count+=n&1; 
		n>>=1; 
	}
	cout<<nn<<"包含"<<count<<"个1"<<endl;
}

int main(){
//	test1();
//	test2();
//	test3();
//	test4();
//	test5();
//	test6();
//	test7();
//	test8();
//	test9();
//	test10();
//	test11();
//	test12();
//	test13(); 
	test14();
}

功能	示例	位运算
去掉最后一位	(101101->10110)	x >> 1
在最后加一个0	(101101->1011010)	x << 1
在最后加一个1	(101101->1011011)	x << 1+1
把最后一位变成1	(101100->101101)	x | 1
把最后一位变成0	(101101->101100)	x | 1-1
最后一位取反	(101101->101100)	x ^ 1
把右数第k位变成1	(101001->101101,k=3)	x | (1 << (k-1))
把右数第k位变成0	(101101->101001,k=3)	x & !(1 << (k-1))
右数第k位取反	(101001->101101,k=3)	x ^ (1 << (k-1))
取末三位	(1101101->101)	x & 7
取末k位	(1101101->1101,k=5)	x & (1<< k -1)
取右数第k位	(1101101->1,k=4)	x >> (k-1) & 1
把末k位变成1	(101001->101111,k=4)	x | (1 << k-1)
末k位取反	(101001->100110,k=4)	x ^ (1 << k-1)
把右边连续的1变成0	(100101111->100100000)	x & (x+1)
把右起第一个0变成1	(100101111->100111111)	x | (x+1)
把右边连续的0变成1	(11011000->11011111)	x | (x-1)
取右边连续的1	(100101111->1111)	(x ^ (x+1)) >> 1
去掉右起第一个1的左边	(100101000->1000)	x & (x ^ (x-1))