电子学会六级-数据结构-离散化
电子学会六级-数据结构-离散化
离散化
离散化是一种数组处理编程技巧
有些数据因为本身很大或者类型不支持,自身无法作为数组的下标来方便地处理,而影响最终结果的只有元素之间的相对大小关系时,我们可以将原来的数据按照从大到小编号来处理问题,即离散化
用来离散化的可以是大整数、浮点数、字符串
离散化目的是将较大区间的个体映射到较小的区间中,提升空间效率,常用来求当前位置的数在源序列的相对位置
https://www.bilibili.com/video/BV1E3411W7G5
校门外的树
http://noi.openjudge.cn/ch0106/06/
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[10001];
int l,m,x,y,s=0;
scanf("%d%d",&l,&m);
for(int i=0;i<=l;i++){// 0-l包括l+1种树位置
a[i]=1;//都赋值为1表示都种树
}
for(int i=1;i<=m;i++){//m段修地铁
scanf("%d%d",&x,&y);//每段起始
for(int j=x;j<=y;j++){//每段起始位置包括中间数都不能种树
a[j]=0;//不能种树的地方设置为0 可能有重复的多次设置为0
}
}
for(int i=0;i<=l;i++){// 0-l包括l+1种树位置
if(a[i]==1) s++; //可以种树的位置累加到s
}
printf("%d",s);
return 0;
}
火烧赤壁
https://www.luogu.com.cn/problem/P1496

二分实现离散化
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=20050;
bool vis[maxn*2];
//len 存储p数组的长度
int n,len;
ll ans=0;
ll l[maxn];//存每艘船的左边坐标,将其离散化之后再存回l中
ll r[maxn];//同l,但是存右边坐标
ll p[maxn*2];//算法分析2中的p数组
/*
二分 在离散后的p数组中 查找v在p中的下标
*/
int search(int x,int y,ll v){
int m;
while(x<y){
m=x+(y-x)/2;
if(p[m]==v) return m;
else if(p[m]>v) y=m;
else x=m+1;
}
return -1;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){//输入n条着火信息
cin>>l[i];//一条着火位置起点
cin>>r[i];//一条着火位置终点
p[len++]=l[i];//起点存入p数组
p[len++]=r[i];//终点存入p数组
}
sort(p,p+len);//p数组排序
for(int i=0;i<n;i++){//离散化后的坐标
l[i]=search(0,len,l[i]);//p数组中找l[i]对应的位置放入l[i]
r[i]=search(0,len,r[i]);//p数组中找r[i]对应的位置放入r[i]
for(int j=l[i];j<r[i];j++)//l[i]~r[i]所有在p中的下标 左闭右开赋值
vis[j]=true;//赋值vis[] true
}
for(int i=0;i<len;i++){//循环查看vis的连续true数
if(vis[i]) ans+=p[i+1]-p[i];//由于左闭右开赋值 区间长度p[i+1]-p[i]
}
cout<<ans;
return 0;
}
二分实现离散化--连续区间长度合并累加
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=20050;
bool vis[maxn*2];
//len 存储p数组的长度
int n,len;
ll ans=0;
ll l[maxn];//存每艘船的左边坐标,将其离散化之后再存回l中
ll r[maxn];//同l,但是存右边坐标
ll p[maxn*2];//算法分析2中的p数组
/*
二分 在离散后的p数组中 查找v在p中的下标
*/
int search(int x,int y,ll v){
int m;
while(x<y){
m=x+(y-x)/2;
if(p[m]==v) return m;
else if(p[m]>v) y=m;
else x=m+1;
}
return -1;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){//输入n条着火信息
cin>>l[i];//一条着火位置起点
cin>>r[i];//一条着火位置终点
p[len++]=l[i];//起点存入p数组
p[len++]=r[i];//终点存入p数组
}
sort(p,p+len);//p数组排序
for(int i=0;i<n;i++){//离散化后的坐标
l[i]=search(0,len,l[i]);//p数组中找l[i]对应的位置放入l[i]
r[i]=search(0,len,r[i]);//p数组中找r[i]对应的位置放入r[i]
for(int j=l[i];j<r[i];j++)//l[i]~r[i]所有在p中的下标 左闭右开赋值
vis[j]=true;//赋值vis[] true
}
// for(int i=0;i<len;i++){//循环查看vis的连续true数
// if(vis[i]) ans+=p[i+1]-p[i];//由于左闭右开赋值 区间长度p[i+1]-p[i]
// }
/*
如果右连续true 累加到变量k
比如下标 1 2 3 对应2 5 8
1.其中1 true 2 true 3 false 2~5=3 5~8=3
则k=3 则长度为:p[k]-[pos]=p[3]-p[1]= 8-2=6
2.其中1 true 2 false 3 false 2~5=3
则k=2 则长度为:p[k]-[pos]=p[2]-p[1]= 5-2=6
*/
int pos=0;
while(pos<len){
if(vis[pos]==0) pos++;
else{
int k=pos;
while(vis[k]) k++;//如果k为true k++ 线段长度记录在起点
ans+=p[k]-p[pos];
pos=k;
}
}
cout<<ans;
return 0;
}
C++ STL 离散化
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=20050;
ll n,cLen=1,uLen,ans=0;
ll L[maxn],R[maxn];//存每艘船的左右边坐标,将其离散化之后再存回l r中
ll c[maxn*2];
ll flag[maxn*2];//标记数组
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>L[i];
cin>>R[i];
c[cLen++]=L[i];
c[cLen++]=R[i];
}
sort(c+1,c+cLen+1);//排序
uLen = unique(c + 1, c + cLen+1) - c - 1;//去重
for(int i=1;i<=n;i++){
L[i]=lower_bound(c+1,c+uLen+1,L[i])-c;//离散化下标
R[i]=lower_bound(c+1,c+uLen+1,R[i])-c-1;//离散化下标 左闭右开 所以 -1
for(ll j=L[i];j<=R[i];j++) flag[j]=1;//标记为true
}
for(int i=1;i<=uLen;i++){//计算每一段标记长度
if(flag[i]) ans+=(c[i+1]-c[i]);
}
cout<<ans;
}
数组存储结构体线段
/*
离散化 就是把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。
通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小
https://www.jianshu.com/p/9347659dcf18
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
struct arr{
int x, y;//起点 终点
}a[maxn];//结构体存储 离散化 不存储无用的连续其他点
int cmp(arr p, arr q){//按起点排序 升序
return p.x < q.x;
}
int ans,n;//ans 累加燃烧的长度和 n起火长度个数
int main(){
scanf("%d",&n);//输入起火的长度个数
for (int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y);//输入每条线段的起点 终点
sort(a+1,a+n+1,cmp);//按起点升序排序
int u = a[1].x, v = a[1].y;//u v记录当前前端的起点和终点
for (int i = 2; i <= n; i++){
if (a[i].x > v){//如果当前的起点>上一个终点 累加上一次 记录本次的u v
ans+= v - u;//累加上一次 到ans
u = a[i].x;
v = a[i].y;//记录本次的u v
}
else if (a[i].y > v) v = a[i].y;//如果x不大于前一次或者前几次 y>v u不变 合并v 线段合并计算
}
ans+= v - u;//累加最后一次线段长度
printf("%d", ans);
}
Blocked Billboard B
https://www.luogu.com.cn/problem/P4122
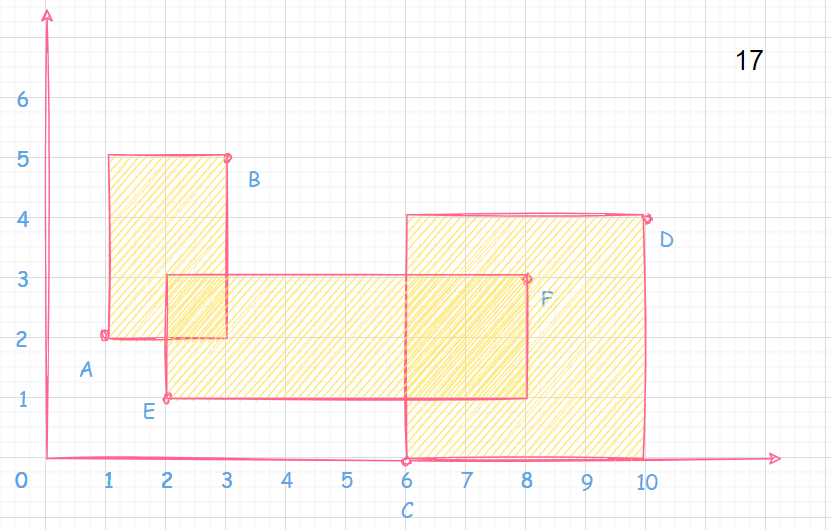
#include <iostream>
#include <algorithm>
using namespace std;
struct Rectangle{//(x1, y1)为左下坐标,(x2, y2)为右上的坐标
int x1, y1, x2, y2;
}A, B, C;
int Area(Rectangle t){//计算矩形面积 长*宽
return (t.x2 - t.x1)*(t.y2 - t.y1);
}
bool check(Rectangle a, Rectangle b){//判断矩形a是否在矩形b内
// 在b左下角右上方 并且在b右上角的左下方 则矩形a在矩形b内
return (a.x1 >= b.x1 && a.y1 >= b.y1
&& a.x2 <= b.x2 && a.y2 <= b.y2);
};
int X[10], Y[10];
int main()
{
cin >> A.x1 >> A.y1 >> A.x2 >> A.y2;
cin >> B.x1 >> B.y1 >> B.x2 >> B.y2;
cin >> C.x1 >> C.y1 >> C.x2 >> C.y2;
//输入6个点的x坐标
X[1] = A.x1, X[2] = A.x2, X[3] = B.x1;
X[4] = B.x2, X[5] = C.x1, X[6] = C.x2;
//输入6个点的y坐标
Y[1] = A.y1, Y[2] = A.y2, Y[3] = B.y1;
Y[4] = B.y2, Y[5] = C.y1, Y[6] = C.y2;
sort(X + 1, X + 7);//对x进行排序
sort(Y + 1, Y + 7);//对y进行排序
int ans = 0;//存放c无法覆盖的a、b面积和
for(int i = 1; i < 6; i ++){//从小到大遍历x
for(int j = 1; j < 6; j ++){//从小到大遍历y
//构造x[i],y[i] -- x[i+1],y[i+1] 最小组成的矩形,可以覆盖a,b,c所有可能的情况
struct Rectangle R = {X[i], Y[j], X[i + 1], Y[j + 1]};
// 判断矩形R在A内 R在B内 且R不在C内的情况
if((check(R, A) || check(R, B)) && !check(R, C))
ans += Area(R);//面积累加到ans
}
}
cout << ans << endl;
return 0;
}
Tallest Cow S
https://www.luogu.com.cn/problem/P2879
程序自动分析
https://www.luogu.com.cn/problem/P1955
过河
https://www.luogu.com.cn/problem/P1052
火柴排队
https://www.luogu.com.cn/problem/P1966
作者:newcode 更多资源请关注纽扣编程微信公众号

从事机器人比赛、机器人等级考试、少儿scratch编程、信息学奥赛等研究学习


 浙公网安备 33010602011771号
浙公网安备 33010602011771号