电子学会二级-二分查找

二分查找

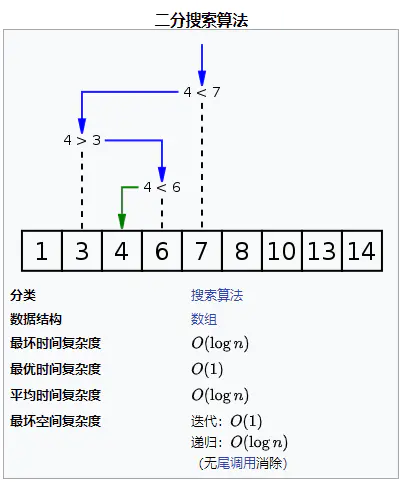
二分查找也叫二分搜索 (binary search)，也叫折半查找 (half-interval search)，是一种在有序数组中查找特定元素的搜索算法。所以用二分查找的前提是数组必须是有序的.

模板1-匹配目标数据

int binarySearch(int a[], int left, int right, int target) {
      while(left <= right) { // 注意
        int mid = (right + left) / 2;
        if(a[mid] == target)
            return mid;
        else if (a[mid] < target)
            left = mid + 1; // 注意
        else if (a[mid] > target)
            right = mid - 1; // 注意
        }
    return -1;
}

right是最后一个有效的下标.搜索区间是[left, right]. 所以while循环中是 " <= "
while(left <= right)的终止条件是 left == right + 1
while(left < right)的终止条件是 left == right

如果有相同数据，匹配到结束，无法匹配最左、最右下标，比如：
数组 a[1, 2, 2, 2, 3]，target = 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

模板2-查询左边界

/*
	左闭右开 [   ) 
	查询左边界 
*/
int left_bound(int a[], int  left, int right, int target) {
    while (left < right) { // 注意
        int mid = (left + right) / 2;
        if (a[mid] >= target) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }

   return left;
}

循环的「搜索区间」是 [left, right) 左闭右开
区间」是 [left, right)左闭右开，所以当 nums[mid] 被检测之后，下一步的搜索区间应该去掉 mid 分割成两个区间，即 [left, mid) 或 [mid + 1, right)
找到 target时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的

模板3-查询左边界

/*
	左开右闭 (    ] 
	查询左边界 
*/
int left_bound2(int a[], int  left, int right, int target) {
    while (left < right) { // 注意
        int mid = (left + right+1) / 2;
        if (a[mid] >= target) {
            right = mid - 1;
        } else {
            left = mid;
        }
    }

   return left;
}

模板4-查询右边界

int right_bound(int a[], int left, int right, int target) {
    while (left < right) {
        int mid = (left + right) / 2;
        if (a[mid] <= target) {
            left = mid + 1; // 注意
        } else if (a[mid] > target) {
            right = mid;
        }
    }

    return left - 1; // 注意
}

模板5

/*
	左开右闭 (    ] 
	查询右边界
*/
int right_bound(int a[], int left, int right, int target) {
    while (left < right) {
        int mid = (left + right+1) / 2;
        if (a[mid] <= target) {
            left = mid; // 注意
        } else if (a[mid] > target) {
            right = mid-1;
        }
    }

    return left - 1; // 注意
}

模板6-左开右开

/*
	左开右开 (    ) 
	出口条件 L+1<R
*/
int binary_search(int a[],int size,int p)
{
    int L = 0;
    int R = size - 1;
    while(R-L > 1){
        int mid = L + (R-L)/2;
        if(a[mid] == p)
            return mid;
        else if(p < a[mid]){
            R = mid;
        }
        else{
            L = mid;
        }
    }
}

切割绳子

#include<iostream>
using namespace std;

int n,m,i,lbound,ubound,mid,count;
int len[100];

int main(){
	cin>>n;
	count=0;
	for(int i=0;i<n;i++){
		cin>>len[i];
//		1
		count=count+len[i];
	}
	cin>>m;
	if(count<m){//  2
		cout<<"Failed"<<endl;
		return 0;
	}
	lbound=1;
//	ubound=1000000;
	ubound=10;
	while(lbound<ubound){//  3
		mid=(lbound+ubound+1)/2;// 4
		count=0;
		for(int i=0;i<n;i++){
			count+=len[i]/mid;
		}
		if(count<m){//分割的数量不到m段  缩小每段长度继续分割 
			ubound=mid-1;//右闭区间 
		}else{
			lbound=mid;//左开区间 
		}
	}
	cout<<lbound<<endl;//输出开区间 
}

/*
n条绳子 分成m段 每条绳子长度已知
5
1 2 3 4 5
2
*/

郊游活动

#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000000
int n,B,A,M[MAXN],C[MAXN],L,R,ans,mid;

bool check(int nn){
	int count=0,i,j;
	i=n-nn+1;//1
	j=1;
	while(i<=n){
		if(M[i]<C[j])// 2  M[i]<=C[j]
			count+=C[j]-M[i];
		i++;
		j++;
	}
	return count<=A;//3
}

void sort(int a[],int L,int R){
	int i=L,j=R,x=a[(L+R)/2],y;
	while(i<=j){
		while(a[i]<x)
			i++;
		while(a[j]>x)
			j--;
		if(i<=j){
			y=a[i];
			a[i]=a[j];
			a[j]=y;
			i++;
			j--;
		}
	}
	if(i<R)
		sort(a,i,R);
	if(L<j)
		sort(a,L,j);
}
int main(){
	int i;
	cin>>n>>B>>A;//n名同学 B辆自行车 学校经费A元 
	for(i=1;i<=n;i++)//n名同学自带钱数组 
		cin>>M[i];
	for(i=1;i<=B;i++)//B辆自行车租赁费用 
		cin>>C[i];
	sort(M,1,n);
	sort(C,1,B);
	L=0;
	R=n;
	while(L<=R){
		mid=(L+R)/2;
		
		if(check(mid)){//4
			ans=mid;
			L=mid+1;//左闭 
		}else
			R=mid-1;//5 右闭 
	}
	cout<<ans;//需要借助n输出 
	return 0;
}
/*
1.输入 
3 2 100
20 10 15
60 70
输出 
2

2.输入
3 2 100
20 10 15
70 80
输出
1
*/

中位数

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1000;
int n,i,lbound,rbound,mid,m,count;
int x[MAXN];
int main(){
	cin>>n>>m;
	for(int i=0;i<n;i++)
		cin>>x[i];
	lbound=0;
	rbound=m;
	while(lbound<rbound){// 1
		mid=(lbound+rbound)/2;
		count=0;// 2 
		for(i=0;i<n;i++)
			if(x[i]>mid)// 3
				count++;// 4
		if(count>n/2)
			lbound=mid+1;//左闭 
		else
			rbound=mid;//5 右开 
	}
	cout<<rbound<<endl;//输出需要明确 不是mid+1或者-1的一边 否则需要ans替换

矩形计数

#include<stdio.h>

struct point{
	int x,y,id;
};

int equals(struct point a,struct point b){
	return a.x==b.x && a.y==b.y;
}

int cmp(struct point a,struct point b){
//	return ①;
	return equals(a,b)?a.id<b.id:a.x<b.x;
}

void sort(struct point A[],int n){
	for(int i=0;i<n;i++)
		for(int j=1;j<n;j++)
			if(cmp(A[j,a[j-1]])){
				struct point t=A[j];
				A[j]=A[j-1];
				A[j-1]=t; 
			}
}

int unique(struct point A[],int n){
	int t=0;
	for(int i=0;i<n;i++)
		//if(②)
		if(t==0||!equals(A[i],A[t-1]))
			A[t++]=A[i];
	return 0;
}

int binary_search(struct point A[],int n,int x,int y){
	struct point p;
	p.x=x;
	p.y=y;
	p.id=n;
	int a=0,b=n-1;
	while(a<b){
//		int mid=③;
		int mid=(a+b)>>1;
//		if(④)
		if(cmp(A[mid],p))
			a=mid+1;
		else
			b=mid;
	}
	return equals(A[a],p);
}

#define MAXN 1000
struct point A[MAXN];

int main(){
	int n;
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d %d",&A[i].x,&A[i].y);
		A[i].id=i;
	}
	sort(A,n);
	n=unique(A,n);
	int ans = 0;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
//			if( ⑤ && binary_search(A,n,A[i].x,A[j].y) && binary_search(A,n,A[j].x,A[i].y)){
			if(A[i].x<A[j] && A[i].<A[j].y && binary_search(A,n,A[i].x,A[j].y) && binary_search(A,n,A[j].x,A[i].y)){
				ans++;
			}
	printf("%d\n",ans);
	return 0;
}