电子学会七级-数据结构-图
Dijkstra
把整个集合分成两部分,确定的最短路点集合、未确定最短路点集合
在未确定最短路的点中,确定一个点,对这个点对应的邻接点进行松弛操作
视频
https://www.bilibili.com/video/BV1zz4y1m7Nq?share_source=copy_web
https://www.bilibili.com/video/BV16R4y1T7tC/?spm_id_from=333.788
为啥不能处理负权?
首先我们要清楚一个点:Dijkstra是每次贪心的选择跟当前邻接的点,而不会去考虑处邻接之外的其他点
而如果所有Dijkstra算法适用于不存在负权边的图(有无向均可),这个是因为迪杰斯特拉算法是基于贪心策略,每次都找一个距源点最近的点,然后将该距离定为这个点到源点的最短路径;但如果存在负权边,那么直接得到的最短路不一定是最短路径,因为可能先通过并不是距源点最近的一个次优点,再通过一个负权边,使得路径之和更小,这样就出现了错误。如下:
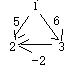
1——>2权值为5,1——>3权值为6,3——>2权值为-2,求1到2的最短路径时,Dijkstra就会选择权为5的1——>2,但实际上1——>3——>2才是最优的结果。
另外如果包含负环,则意味着最短路径不存在。因为只要在负权回路上不断兜圈子,所得的最短路长度可以任意小。负数的绝对值越大,该值就越小。
https://www.luogu.com.cn/problem/P1339
#include<bits/stdc++.h>
using namespace std;
const int maxn=2510;
int G[maxn][maxn];//邻接矩阵
int dist[maxn];//存储源点到i的最短长度
bool vis[maxn];//v[i]存储节点i是否已确定最小路径
int n,m,s,t;//n个点 m条边 s源点 t目标点
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(G,0x7f,sizeof(G));
memset(vis,true,sizeof(vis));
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
G[x][y]=G[y][x]=z;
}
memset(dist,0x7f,sizeof(dist));
dist[s]=0;//开始到源点距离为0
for(int i=1;i<=n;i++){//找出每个点的最短路
//找当前最短路的最小值 //默认最大值 从1开始 0不使用 dist[0]为0x7f 最大值
int k=0;
for(int j=1;j<=n;j++){
if(dist[j]<dist[k] &&vis[j]){//找为确定所有节点最小距离
k=j;//更新最小
}
}
vis[k]=false;//k点的最小路径长度确定了
if(k==t) break;//确定到e的最短路径 结束
for(int j=1;j<=n;j++){//松弛i节点后续的节点 更新d数组值
if(dist[k]+G[k][j]<dist[j]){
dist[j]=dist[k]+G[k][j];
}
}
}
printf("%d\n",dist[t]);
return 0;
}
单源最短路径(标准版)
https://www.luogu.com.cn/problem/P4779
Dijkstra 优先队列 邻接表优化
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n,m,s;//n个点m条边 从s点出发
int dist[maxn];
struct node{
int y,w;//y 目标点 w源点到目标点的长度
node(int y=0,int w=0):y(y),w(w){};//构造函数
bool operator < (const node &p) const {//结构体运算符重载 p为堆顶元素 w>p.w为小顶堆
return w>p.w;
}
};
vector<node> e[maxn];//邻接表
void dijkstra(int s){
memset(dist,0x3f,sizeof(dist));//初始赋最大值
dist[s]=0;//源点到源点距离为0
priority_queue<node> q;//优先队列
q.push(node(s,0));//开始节点放入优先队列
while(!q.empty()){
node top=q.top();
int k=top.y;
q.pop();
if(top.w>dist[k]) continue;//多次松弛 放入队列的部分不是最小的不处理
for(int i=0;i<e[k].size();i++){//松弛操作 找当前最短路节点所有邻接边
int y=e[k][i].y;
int w=e[k][i].w;
if(dist[k]+w<dist[y]){//通过当前最短路节点比原来的小 可松弛
dist[y]=dist[k]+w;//用较小替换原来的值
q.push(node(y,dist[y]));//加入优先队列 尝试判断进入已确定集合
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&s);//n个点 m条边 从s点开始
for(int i=1;i<=m;i++){//循环每条边
int u,v,w;//u到v有一条边 边权为w
scanf("%d%d%d",&u,&v,&w);//输入
e[u].push_back(node(v,w));//构造邻接表
}
dijkstra(s);//调用函数 计算从s开始到个点的最短路径距离
for(int i=1;i<=n;i++){//输出到i最短路径距离
printf("%d ",dist[i]);
}
}
https://www.luogu.com.cn/problem/P1346
https://www.luogu.com.cn/problem/P1821
Bellman-Ford算法
随机松弛边,有盲目性,对应优化算法SPFA
Bellman-Ford 为什么需要n-1次循环
https://www.cnblogs.com/myeln/articles/16291775.html
https://www.luogu.com.cn/problem/P1744
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
const int M = 1005;
int x[N], y[N];// x 每家点横坐标 y每家点纵坐标
double dis[N];// 到i点的最短路径
int n, m, s, t;//n所有点数 m所有边数 s源点 t目标点
double get_dis(int k1, int k2){//计算两坐标之间距离
return sqrt((x[k1]-x[k2])*(x[k1]-x[k2])+(y[k1]-y[k2])*(y[k1]-y[k2]));
}
struct Edge{//边结构体
int u, v;//u 边起点 v边终点
double w;//边长
Edge(int U =0, int V=0, double W = 0.0) {//构造函数 方便构造边
u=U; v= V; w=W;
}
}e[M << 1];//无向图 边为 2*M 构造e为边集数组
void bellman_ford(int s){//从
for(int i=1;i<=n;i++)
dis[i]=0x3f3f3f3f;//
dis[s]=0;//到起点的最短路径为0
for(int i=1;i<=n-1;i++)//更新n-1次
for(int j=1;j<=m;j++){//更新每一条边
Edge &ei = e[j];//结构体变量简化如下写法
if(dis[ei.u] + ei.w < dis[ei.v]){//到u最短路径+uv边<之前到v的最短路径 松弛
dis[ei.v] = dis[ei.u] + ei.w;//松弛 到v的最短路径长度使用经过u的路径
}
}
}
int main(){
cin >> n;//n个点
for(int i=1;i<=n;i++){//读取所有坐标点
cin>>x[i]>>y[i];
}
cin>>m;//m条边
for(int i=1;i<=m;i++) {
int u,v;//u 起点 v终点 w边长
cin>>u>>v;
double w;
w=get_dis(u,v);
e[i]=Edge(u,v,w);//构造一条边 起点 终点 边长
e[i+m]=Edge(v,u,w);//构造反向边
}
cin>>s>>t;//输入 s源点 t目标点
m <<= 1;//无向图 变数 m*2
bellman_ford(s);//调用bellman ford算法计算最短路
printf("%.2lf", dis[t]);//输出到目标点t的最短路径长度
return 0;
}
SPFA算法
从源点开始松弛每条边 邻接点被松弛 就加入队列尝试松弛被松弛点的邻接点
https://www.luogu.com.cn/problem/P3371
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+100;
struct node{//结构体
int y,w;//y终点 w起点到终点的边权
node(int yy,int ww){//构造函数 构造时赋值 方便后续赋值 简化代码
y=yy;
w=ww;
}
};
bool v[maxn];//是否能放入队列
vector<node> e[maxn];//邻接矩阵
int d[maxn];//源点到目标点的距离
int n,m,s;//n节点数 m边数 s起始节点编号
//spfa算法计算所有源点到可达目标点的最短路径长度
void spfa(int s){
memset(d,0x3f,sizeof(d));
memset(v,true,sizeof(v));
d[s]=0;
queue<int> q;//存放被松弛过的点
q.push(s);
v[s]=false;
while(!q.empty()){//队列有被松弛的点 继续
//取队列头
int x=q.front();
q.pop();
v[x]=true;//出队设置可以放入队列
//松弛x邻接点
for(int i=0;i<e[x].size();i++){
int y=e[x][i].y;
int w=e[x][i].w;
//松弛邻接节点 他们的边权是w
if(d[x]+w<d[y]){
d[y]=d[x]+w;
//加入队列是为了松弛邻接点 既然已经在队列 出队时自然可以松弛 没必要重复添加
//此时d[y] 已经被改变 出队时松弛计算就是最小
if(v[y]==true){//不在队列 可以松弛 则加入队列
q.push(y);//加入队列
v[y]=false;//加入队列后 设为false 不允许队列中存在多个
}
}
}
}
}
int main(){
cin>>n>>m>>s;//输入n个点 m条边 s编号
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
e[x].push_back(node(y,z));//邻接表构建
}
spfa(s);// spfa算法计算s开始到可达点的最短路径长度
for(int i=1;i<=n;i++){
if(d[i]==d[0]){//如果不可达 输出2的31次方-1
cout<<(1<<31)-1<<' ';
}else{
cout<<d[i]<<' ';//输出最短路径长度
}
}
}
https://www.luogu.com.cn/problem/P3385
判断负环
//从起点, 经过最短路径到终点, 期间最多经过 N-1 个结点. 如果超过N个, 则一定有负环.
//用 times[x] 表示 1 到 x 的最短路包含的边数,times[1]=0。每次用 dis[x]+w(x,y) 更新 dis[y] 时,
//也用 times[x]+1 更新 times[y]。此过程中若出现 cnt[y]≥n,则图中有负环。最坏情况复杂度也是 O(nm)。
#include<bits/stdc++.h>
const int INF=0x3f3f3f3f;
const int maxn=2001;
using namespace std;
struct edge{
int v,w;
edge(int _v=0,int _w=0){//构造函数
v=_v;
w=_w;
}
};
int n;
vector<edge>g[maxn];//邻接表
int d[maxn];
bool vis[maxn];
queue<int>q;
int times[maxn];//记录松弛次数
void spfa(int s){
memset(vis,0,sizeof(vis));
memset(d,INF,sizeof(d));//d数组从最大开始松弛
memset(times,0,sizeof(times));
while (!q.empty()) q.pop();//多组数据,处理前要全部清空
q.push(s);//从s点开始
vis[s]=1;//已经放入
d[s]=0;//源点到s为0
times[s]=1;//s点更新
while (!q.empty()) {
int now=q.front();
q.pop();
vis[now]=0;
for(int i=0;i<g[now].size();i++){//遍历now起点的邻接点
int v=g[now][i].v;//终点
int w=g[now][i].w;//长度
if(d[v]>d[now]+w){//到v最短路径>到now最短路径 +w now+此边 比原来小 松弛
d[v]=d[now]+w;
times[v]++;//经过v点次数+1
if(times[v]>n){//经过v点次数>n
puts("YES");//说明有负环,输出YES
return;//返回,不需要继续遍历
}
if(!vis[v]){//松弛时 v点不在队列
q.push(v);//加入队列
vis[v]=1;//打标不能加入队列
}
}
}
}
puts("NO");//永远没有点松弛次数大于n,说明无负环
}
int main()
{
int t,m;
scanf("%d",&t);//t 组数据
for (int i=1;i<=t;i++){//循环处理每组数据
scanf("%d%d",&n,&m);//n 节点数 m边的条数
int u,v,w;//u起始节点 v终点节点 w边权
for (int j=1;j<=m;j++){
scanf("%d%d%d",&u,&v,&w);//输入
g[u].push_back(edge(v,w));//构造邻接表数据
if (w>=0) g[v].push_back(edge(u,w));//大于等于0时双向边 --根据录入条件说明
}
spfa(1);//调用函数,起点为1
for (int j=1;j<=n;j++)
g[j].clear();//清空
}
return 0;
}
https://www.luogu.com.cn/problem/P1359
https://www.luogu.com.cn/problem/P1339
多源最短路 弗洛伊德 Floyd算法
https://www.luogu.com.cn/problem/P2935
#include<bits/stdc++.h>
using namespace std;
const int maxn=510;
int f[maxn][maxn];//f[i][j] 表示i到j的最小路径
int a[maxn];//存储喜欢的牧场
int n,s,m;//n个牧场 s个喜欢的牧场 m条无向边
int main(){
cin>>n>>s>>m;//n个牧场 s个喜欢的牧场 m条无向边
for(int i=1;i<=s;i++){//记录所有喜欢的牧场
cin>>a[i];
}
memset(f,0x30,sizeof(f));//最小路径默认无穷大
for(int i=1;i<=n;i++){//自己到自己的最短路径为0
f[i][i]=0;
}
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
if(z<f[x][y]){//赋值两点间最短路径
f[x][y]=f[y][x]=z;//无向图赋值
}
}
//弗洛伊德算法核心 Floyd
for(int k=1;k<=n;k++){// 每个途径点 刷新一次矩阵
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(f[i][k]+f[k][j]<f[i][j]){//i~k最短路+k~j最短路比i~j的最短路小 更新i~j最短路
f[i][j]=f[i][k]+f[k][j];//更新i~j最短路
}
}
}
}
int k=0,ans=1e9;//k记录 住k处 到喜欢牧场最短路径和最小的牧场编号 ans记录 住k处 到喜欢牧场最短路径和
for(int i=1;i<=n;i++){
int sum=0;//从i出发到所有喜欢点的最短路径和
for(int j=1;j<=s;j++){
sum+=f[i][a[j]];
}
if(sum<ans){//i到所有喜欢牧场最短路径和比ans小 更新ans
ans=sum;//更新ans
k=i;//更新牧场编号
}
}
cout<<k;
return 0;
}
https://www.luogu.com.cn/problem/P2910
https://www.luogu.com.cn/problem/P1359
https://www.luogu.com.cn/problem/P2419
https://www.luogu.com.cn/problem/P2888
最小生成树 -Kruskal
https://www.luogu.com.cn/problem/P2330
#include<bits/stdc++.h>
using namespace std;
const int maxn=310;
const int maxm=1e5+10;
struct edge{//边集数组
int x,y,w;//起点 终点 长度
}e[maxm];
int n,m;
int f[maxn];//i点父节点编号
//从x找根 路径压缩算法 不是根 把自己挂在根下面
int find(int x){
if(f[x]!=x){// 父节点不是自己 即不是根
f[x]=find(f[x]);//通过父节点找根 并把根赋值给x的父节点 x加入根节点子节点 路径压缩
}
return f[x];
}
bool cmp(edge P,edge Q){
return P.w<Q.w;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].w);//m条道路 起始点 终点 边权
}
sort(e+1,e+m+1,cmp);//按边权从小到大排序
for(int i=1;i<=n;i++){
f[i]=i;//i的父节点设置自己 所有节点初始为根节点
}
int cnt=0;
for(int i=1;i<=m;i++){//遍历m条边
int rx=find(e[i].x);//找x根节点
int ry=find(e[i].y);//找y的根节点
if(rx!=ry){//根不同 不连通 可以加入连通
if(++cnt==n-1){
printf("%d %d\n",n-1,e[i].w);//分值最大的道路分值 最后的一条 已排序
return 0;
}
f[rx]=ry;//连通 fx的父节点指向ry rx和ry有一个根节点 连通
}
}
}
https://www.luogu.com.cn/problem/P3366
https://www.luogu.com.cn/problem/P1265
图
http://noi.openjudge.cn/ch0308/
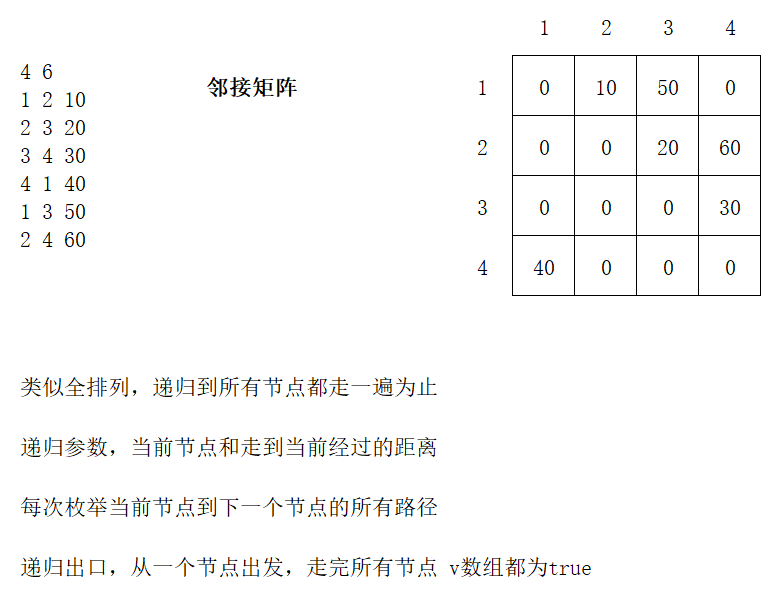
邻接矩阵
https://www.luogu.com.cn/problem/P1294
题解
#include<iostream>
using namespace std;
const int maxn = 30;
int G[maxn][maxn];//邻接矩阵 G[i][j] 表示i-j的距离
int vis[maxn];//一次方案中是否使用过某个节点
int n,m,ans;//ans表示某方案最大距离
//u从某节点开始 sum到当前节点最大距离
void dfs(int u,int sum) {
if(sum>ans) ans=sum;
for(int i=1;i<=n;i++)//找所有可以发的下一个节点
if(!vis[i] && G[u][i]) {//!vis i没被使用过 且G[u][i] u-i有路(距离不为0)
vis[i]=1;//i节点占住
dfs(i,sum+G[u][i]);//递归下一层节点
vis[i]=0;//i节点释放
}
}
int main() {
cin>>n>>m;
int u,v,w;
for(int i=0;i<m;i++) {
cin>>u>>v>>w;
G[u][v]=G[v][u]=w;//有向图 u~v=w 且 v~u=w
}
for(int i=1;i<=n;i++) {
vis[i]=1;//占用此节点
dfs(i,0);//从第一个节点开始作为第一个方案
vis[i]=0;//释放此节点
}
cout<<ans;//输出最大距离
return 0;
}
https://www.luogu.com.cn/problem/P1199
//https://www.luogu.com.cn/blog/wjyyy/solution-p1199
//https://my.oschina.net/u/4414193/blog/3915091
//博弈 最优都拿不到 可以选择拿到最优勇士对应的次最大 可以被人拿到
#include<bits/stdc++.h>
using namespace std;
int G[510][510];//邻接矩阵
int main(){
int n;
scanf("%d",&n);//武将个数
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
scanf("%d",&G[i][j]);//武将组合默契值 A -> B
G[j][i]=G[i][j];//武将组合默契值 B -> A
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
sort(G[i]+1,G[i]+1+n);//每列选取最优勇士
ans=ans>G[i][n-1]?ans:G[i][n-1];//选出排名第二中最大的那个
}
printf("1\n%d\n",ans);//一定有解
return 0;
}
拓扑排序
https://www.luogu.com.cn/problem/P1137
/*
一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,
是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),
则u在线性序列中出现在v之前。 (源自百度)
通俗的说就是,一张有向无环图的拓扑序可以使得任意的起点u,它的一个终点v,
在序列中的顺序是u在前v在后
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=100000+15;
int n,m,sum,tot;//n个城市 m条道路 sum边
//head[] 下标为起点 value为最后一个终点edge
//ru[] 记录每个点入度
//ts 排序好的拓扑序列
//dp 到节点i可以访问最多城市数
int head[maxn],ru[maxn],ts[maxn],dp[maxn];
struct EDGE{
int to;//边的终点
int next;//
}edge[maxn<<2];
void add(int x,int y){//链式前向星加边
edge[++sum].next=head[x];//增加一条边 next为前一个 插入前面
edge[sum].to=y;//加入终点
head[x]=sum;//head移动到当前
}
void topsort(){//拓扑排序
queue <int> q;
for (int i=1;i<=n;i++){//入度为0放入队列
if (ru[i]==0) {
q.push(i);
ts[++tot]=i;//记录topo排序节点
}
}
while (!q.empty()){//队列不为空
int u=q.front();q.pop();//出队
for (int i=head[u];i;i=edge[i].next){// 遍历以u出去的边
int v=edge[i].to;//终点 v
ru[v]--;//删除u v边 v出度减1
if (ru[v]==0) {//如果减1后v出度为0,加入队列
q.push(v);ts[++tot]=v;//加入topo排序的节点
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
ru[v]++;//加一条边 终点入度加1
}
topsort();
for (int i=1;i<=n;i++) dp[i]=1;//赋初值 默认到达城市为1
for (int i=1;i<=n;i++){//遍历所有节点
int u=ts[i];//按拓扑序列遍历
for (int j=head[u];j;j=edge[j].next){//遍历临接点
int v=edge[j].to;//v 目标点
dp[v]=max(dp[v],dp[u]+1);//到起始点 和目标点 取最大 可以访问的节点取最大
}
}
for (int i=1;i<=n;i++)//到i城市最多游览城市数
printf("%d\n",dp[i]);
return 0;
}
https://www.luogu.com.cn/problem/P3371
https://www.luogu.com.cn/problem/P1608
链式前向星
参考拓扑排序
https://www.luogu.com.cn/problem/P1137
边集数组
参考 Bellman-Ford算法
https://www.luogu.com.cn/problem/P1744
邻接表
https://www.luogu.com.cn/problem/P1199
https://www.luogu.com.cn/problem/P1137
https://www.luogu.com.cn/problem/P3916
链式前向星
https://www.luogu.com.cn/problem/U81206
https://www.luogu.com.cn/problem/P2661
https://www.luogu.com.cn/problem/P1351
https://www.luogu.com.cn/problem/P1197
图的基本应用
https://www.luogu.com.cn/problem/P5318
https://www.luogu.com.cn/problem/P1113
https://www.luogu.com.cn/problem/P4017
https://www.luogu.com.cn/problem/P1807
https://www.luogu.com.cn/problem/P2853
https://www.luogu.com.cn/problem/P1983
基础树上问题
https://www.luogu.com.cn/problem/P5836
https://www.luogu.com.cn/problem/P3629
https://www.luogu.com.cn/problem/P3379
https://www.luogu.com.cn/problem/P5536
最短路
https://www.luogu.com.cn/problem/P3371
https://www.luogu.com.cn/problem/P4779
https://www.luogu.com.cn/problem/P1629
https://www.luogu.com.cn/problem/P1144
https://www.luogu.com.cn/problem/P1522
最小生成树
https://www.luogu.com.cn/problem/P3366
https://www.luogu.com.cn/problem/P2872
https://www.luogu.com.cn/problem/P1396
https://www.luogu.com.cn/problem/P2121
https://www.luogu.com.cn/problem/P1194
https://www.luogu.com.cn/problem/P1195
https://www.luogu.com.cn/problem/P4047
连通性问题
https://www.luogu.com.cn/problem/P3387
https://www.luogu.com.cn/problem/P3388
https://www.luogu.com.cn/problem/P2341
https://www.luogu.com.cn/problem/P2863
https://www.luogu.com.cn/problem/P1726
算法训练营
https://vjudge.net/article/2652
图的存储
https://vjudge.net/problem/洛谷-P3916
https://vjudge.net/problem/UVA-11175
https://vjudge.net/problem/POJ-3275
图的遍历
https://vjudge.net/problem/UVA-572
https://vjudge.net/problem/UVA-1599
https://vjudge.net/problem/POJ-2488
https://vjudge.net/problem/POJ-3278
图的连通性
图的应用
最短路径
最小生成树
拓扑排序
关键路径
作者:newcode 更多资源请关注纽扣编程微信公众号

从事机器人比赛、机器人等级考试、少儿scratch编程、信息学奥赛等研究学习



 浙公网安备 33010602011771号
浙公网安备 33010602011771号