电子学会三级-递归

菲波那契数列

题解

由题意知，数列第一个数和第二个数都是1，第三个数开始，当前数为前两个数之和

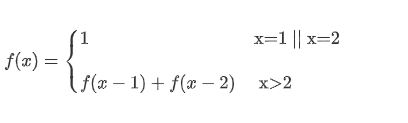
#include<bits/stdc++.h>
using namespace std;

int fib(int n){
	if(n==1 || n==2){
		return 1;
	}
	return fib(n-1)+fib(n-2);
}

int n,m;
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>m;
		cout<<fib(m)<<endl;
	}
}

爬楼梯

题解

由题意知，走1级楼梯方法数是1，走2级楼梯方法数是2，第3级开始，当前数为前两个数之和

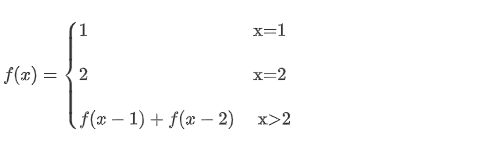
#include<bits/stdc++.h>
using namespace std;

int cs(int n){
	if(n==1){
		return 1;
	}
	if(n==2){
		return 2;
	}
	return cs(n-1)+cs(n-2);
}
int n;
int main(){
	while(cin>>n){
		cout<<cs(n)<<endl;
	}
} 

Pell数列

题解

由题意知，a₁为1，a₂为2，a_n=2*a_n-1+a_n-2,另外数列结果可能比较大，需要进行对32767取模。

由数论加法取模运算规则：

(a+b) mod n=(a mod n+b mod n) mod n

可以在每次递归进行取模

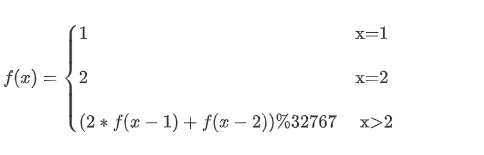
#include<bits/stdc++.h>
using namespace std;
int a[1000001];//递归优化 防止每次计算
int pell(int num){
	if(a[num]!=0) return a[num];
	if(num==1){
		a[1]=1;
		return 1;
	}
	if(num==2){
		a[2]=2;
		return 2;
	}
	a[num]= (2*pell(num-1)+pell(num-2))%32767;
	return a[num];
}

int main(){
	int n;
	cin>>n;
	for(int i=0;i<n;i++){
		int temp;
		cin>>temp;
		cout<<pell(temp)<<endl;
	}
	return 0;
}

求最大公约数问题

题解

辗转相除法， 又名欧几里德算法（Euclidean algorithm）

是求最大公约数的一种方法。它的具体做法是：用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止

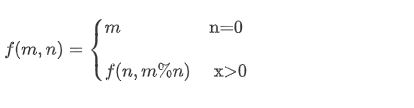
#include<bits/stdc++.h>
using namespace std;
//求最大公约数可以使用辗转相除法：
//假设a > b > 0，那么a和b的最大公约数等于b和a%b的最大公约数，然后把b和a%b作为新一轮的输入。
//由于这个过程会一直递减，直到a%b等于0的时候，b的值就是所要求的最大公约数。
//比如：
//9和6的最大公约数等于6和9%6=3的最大公约数。
//由于6%3==0，所以最大公约数为3。
int gcd(int a,int b){
	if(b==0) return a;
	
	return gcd(b,a%b);
}
int x,y;
int main(){
	cin>>x>>y;
	cout<<gcd(x,y);
} 

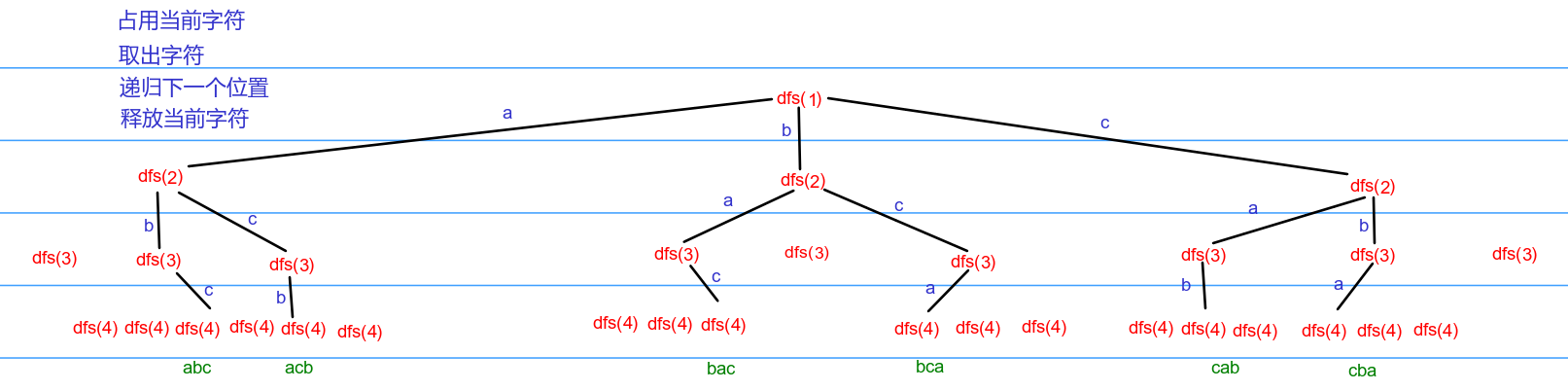
7150 全排列

题解

n个数的全排列：从n个不同元素中任取n个元素，按照一定的顺序排列起来

1.每一种方案需要填满n个数，从第一个数开始填，填之前需要判断当前字符是否已经被使用，未被使用的字符才能组成本次方案

由于一次方案中不能重复，因此已经填过的数需要打标记，我们可以使用一个数组：b[1000] ; b[a]=1表示a已经使用 b[a]=0 表示a未使用

2.填写到当前位置

3.递归填写下一个位置

4.释放当前字符 b[a]=0

#include<bits/stdc++.h>
using namespace std;

bool b[10001];//字符是否被用过
//s 输入的字符数组 ans本来输出的字符数组 
char s[10001],ans[10001];
int len;//字符输入长度 
//填第depth个数 
void dfs(int depth){
	//递归到长度+1个字符处理输出 比实际多一个 
	if(depth==len+1){
		for(int i=1;i<len+1;i++){
			printf("%c",ans[i]);
		}
		printf("\n");
		return;
	}
	//每个位置用数组中的字符填一遍 
	for(int i=0;i<len;i++){
		if(b[s[i]]==false){//本轮此字符是否被用过 
			b[s[i]]=true;//标记此字符已经使用 
			ans[depth]=s[i];//记录此字符到本来数组中 
			dfs(depth+1);//递归下一个位置 
			b[s[i]]=false;//回溯释放此字符(标记此字符可以使用) 
		}
	}
}

int main(){
	scanf("%s",s);
	len=strlen(s);
	dfs(1);//从第一个数开始填 
}

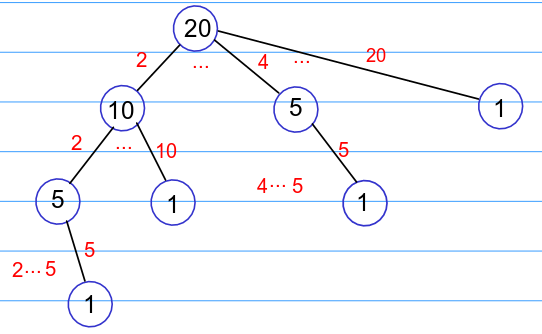
1751 分解因数

题解

由题意知：

1.需要把一个数分解若干个数相乘，并且后面的数比前面的数大

2.可以考虑从符合要求最小整数拆分，逐个去除 20/2 20/3 20/4 ... 20/20

3.除完每个整数后，继续执行2 直到除完结果为1结束，为1个方案 20/2=10 10/2=5 5/5=1

4.1为递归出口，方案数+1

#include<bits/stdc++.h>
using namespace std;

int k,n;//k累加分解方案数 n组数 
//s 被分解数 m 从哪个数开发分解 
void dfs(int s,int m){
	if(s==1){//直到s为1 一种方案完成 
		k++;
		return;
	}else{
		for(int i=m;i<=s;i++){//试除法 
			//可以整除 整除后 继续用i整除
			//不能整除 尝试下一个是否继续整除 
			if(s%i==0){
				dFactor(s/i,i);
			}
		}
	}
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		k=0;
		int t;
		cin>>t;
		dfs(t,2);
		cout<<k<<endl;
	}
}

8758 2的幂次方表示

题解

提前计算2的对应次方的值存入数组
从小于当前数的最大2的次方开始处理 9=8+1 先处理8再处理1
9=8+1=2(3)+2(0) 递归计算3 3=2+2(0)

#include<bits/stdc++.h>
using namespace std;
int a[20];
//提前计算2的对应次方的值存入数组
//从小于当前数的最大2的次方开始处理 9=8+1 先处理8再处理1 
//9=8+1=2(3)+2(0) 递归计算3 3=2+2(0) 
void dfs(int x){
    for(int i=15;i>=0;i--){//从2的15次方开始减  x一定小于2的15次方，保证可以减小于x的2的最大次方 
        if(x-a[i]>=0){
            x-=a[i];
            if(i==1)printf("2");// 1特殊展示 
            else if(i==0)printf("2(0)");//0 递归出口 
            else{//
                printf("2(");
				dfs(i);//可以继续分解括号内容
				printf(")");
            }
            if(x)printf("+");//如果x不是0 后面还可以分解 
            else return;
        }
    }
}
int main(){
    int n;
    cin>>n;
    a[0]=1;
    for(int i=1;i<=15;i++){//提前计算2的0-15次方 存入数组 
    	a[i]=a[i-1]*2;
	}
    dfs(n);    
}