noi 1700 输出 八皇后问题

noi 输出 八皇后问题

http://noi.openjudge.cn/ch0205/1700/

 

思路：

题意知八皇后中 行，列，正斜线对角线 /、反斜线对角线 \都不能存在两个或者两个以上

递归列，每列放一个皇后，放置过程中判断行、正斜线对角线 /、反斜线对角线 \都不能存在两个或者两个以上皇后

行使用数组b判断

反斜线对角线 \  w[i-j+7] 数组判断

正斜线对角线 /  m[i+j]  数组判断

具体可参考如下示例加以理解

 

 

 

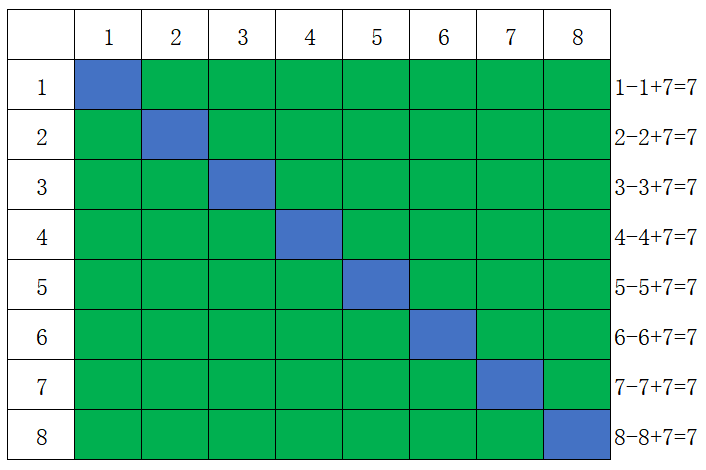
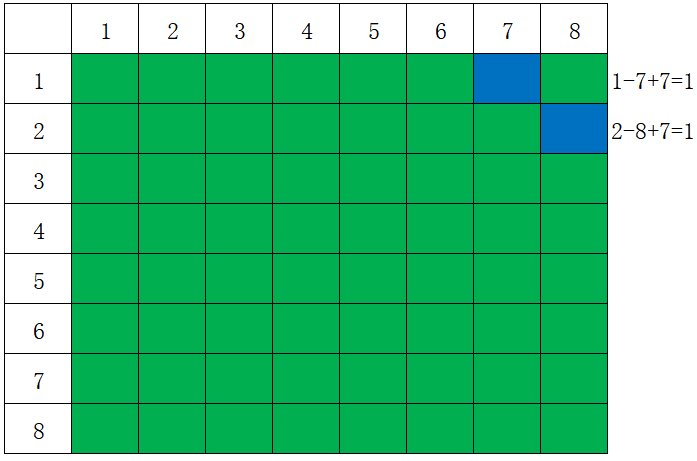
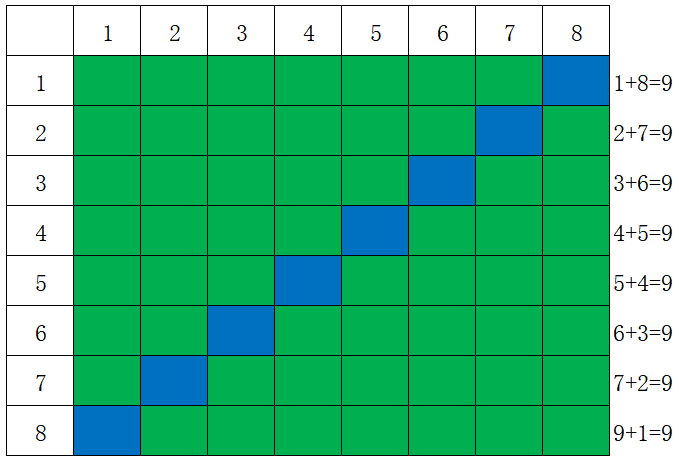
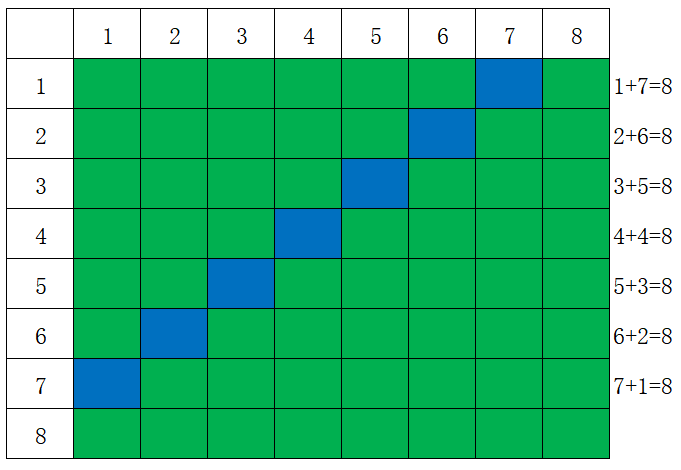
示例程序

#include<bits/stdc++.h>
using namespace std;

int a[10001],b[10001],w[10001],m[10001],tot=0;
int print(){
    tot++;//每输出一次 tot++ 
    cout<<"No. "<<tot<<endl;
    //循环每个皇后 列 
    for(int j=1;j<=8;j++){
        //循环行 对应a[i]是皇后输出 
        for(int i=1;i<=8;i++){
            if(j==a[i]){
                cout<<1<<" ";
            }else{
                cout<<0<<" ";
            }
        }
        cout<<endl;
    }
}
//逐渐深入遍历8列 j为对应列 
int search(int j){
    //循环遍历8行 
    for(int i=1;i<=8;i++){
        //b[i]为0表示这行可放 一次八皇后解中一列只能一个皇后
        //w[i-j+7]为0表示反斜线方向对角线可放 一次八皇后解中某对角线只能放一个皇后
        //m[i+j]为0表示正斜线方向对角线可放 一次八皇后解中某对角线只能放一个皇后
        if(b[i]==0 && w[i-j+7]==0 && m[i+j]==0){
            a[j]=i;//记录每个皇后位置 在第几列 
            b[i]=1;
            w[i-j+7]=1;
            m[i+j]=1;
            if(j==8){//第八个输出 
                print();
            }else{
                search(j+1);
            }
            //回溯 恢复 
            b[i]=0;
            w[i-j+7]=0;
            m[i+j]=0;
        }
    }    
}

int main(){
    search(1);
    return 0;    
}