Luogu7952

前言

✗✓OI TXDY！

NOIP 前一发题解，RP++！

思路

为了建立直观理解，我们尝试对树进行重构。

你考虑这么一件事情，就是说：我们考虑把树三度化，每个结点变成一条向右的链，链上每个结点的左儿子是原树该结点的各个儿子。

我们发现这是一颗二叉树。为简便，我们以下称其为重构树，向右的链称为右链，向左的链称为左链。

我们给出样例 1 的其中一颗重构树：

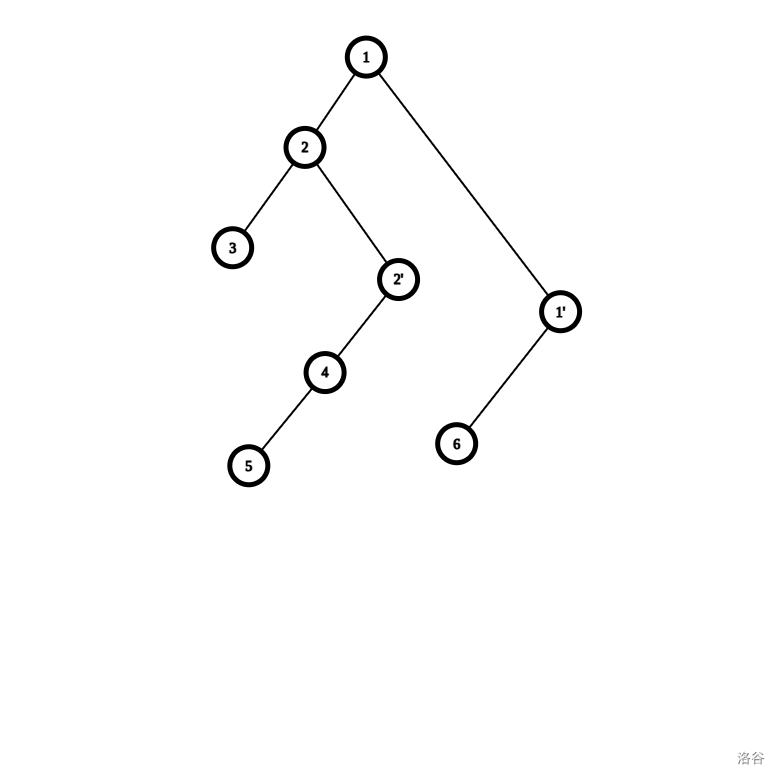
我们规定重构树上每个右链的根结点为实结点，权值为原树上该结点的权值；其余点称为虚结点，权值 \(0\)。虚结点中最下面的称为最末虚结点。

实结点的左儿子称为重左儿子，虚结点左儿子称为轻左儿子。

我们发现，在原树上的 2 操作，在重构树上有简洁的表示！

你考虑这么一件事情，就是说：在重构树上，实结点权值向父亲平移，根节点权值扔掉，未赋值者用 \(0\) 补齐。

这样的话显然虚结点权值可能被赋值，于是将其权值再送给其对应的实结点。

这就是 2 操作在重构树上的表示。

我们发现，对重构树 dfs 序的区间左移一位，与我们上述描述几乎等价！因为虚结点所在的权值 \(0\) 段刚好转移到最新叶结点上了！

对被赋值的虚结点，我们如何更新？

你考虑这么一件事情，就是说：虚结点必定是其父亲的右儿子，且必定有左儿子，因此其必定位于一条左链的顶端。而且，这条左链上必然除了其外都为实结点。我们称最低者为最末实结点。

因此我们动态维护每条左链上还活着的最末实结点，并在修改时动态更新其所在左链根结点即可。

为了得到每个点所在左链根结点，我们可以考虑一个类似树剖的过程：dfs 一遍原树，取重左儿子指向根节点指向的左链链顶，让轻左儿子指向根节点的各个虚结点。

为了保证复杂度，我们必须用 size 来定义重左儿子和轻左儿子，从而获得均摊的复杂度。像上面图例那样就是不可取的。

通过以上描述，我们发现 2 操作被描述成了重构树 dfs 序上的区间平移与若干次单点修改。

放一部分代码理解一下。

uint Fath[1000005];
std::set<uint>Leaf;
std::vector<uint>Insert,Erase,Son[1000005];
uint Bgn[1000005],End[1000005],cnt=1,Belong[3000005],Heavy[1000005],Siz[1000005],Up[1000005],Deg[1000005];
ullt A[1000005];
voi get(uint p)
{
	Siz[p]=1,Heavy[p]=-1,Deg[p]=Son[p].size();
	for(auto s:Son[p]){get(s),Siz[p]+=Siz[s];if(Heavy[p]==-1u||Siz[s]>Siz[Heavy[p]])Heavy[p]=s;}
}
voi dfs(uint p,uint user)
{
    Up[Belong[cnt]=p]=user,Splay::insert(cnt,A[Belong[cnt]]),Bgn[p]=cnt++;
    if(~Heavy[p])dfs(Heavy[p],user);
    for(auto s:Son[p])if(s!=Heavy[p])Splay::insert(cnt,0),Belong[cnt++]=p,dfs(s,cnt-1);
    End[p]=cnt;if(Heavy[p]==-1u)Leaf.insert(Bgn[p]);
}

if(!Splay::find(Bgn[p],End[p]))continue;
Splay::erase(Bgn[p]),Splay::insert(End[p]-1,0);
auto iter=Leaf.upper_bound(Bgn[p]);
while(iter!=Leaf.end()&&*iter<End[p])
{
    uint u(Belong[*iter]);uint t(Up[u]);
    Splay::kth(t);ullt v(Splay::rot->v);
    Splay::rot->v=0,Splay::add(Bgn[Belong[t]],v);
    if(!Deg[u])
    {
	    Erase.push_back(*iter);
        if(!--Deg[Fath[u]]||Up[Fath[u]]==t)Insert.push_back(Bgn[Fath[u]]);
    }
    ++iter;
}
for(auto s:Erase)Leaf.erase(s);
for(auto s:Insert)Leaf.insert(s);
Insert.clear(),Erase.clear();

观察一下重构树上的 dfs 序，发现这本质就是原树欧拉序对每个非叶结点去掉最后一次出现位置的结果。

因此，1 操作被描述成了区间查询 max！

于是，我们的问题就变成了区间平移、单点修改与区间查询 max 的高效实现！

注意到数据范围 \(10^6\)，块状链表似乎不是很有前途，于是毅然弃疗上 Splay，结果因为常数大被卡常了……听说 fhq treap 做法与跳表做法常数很小？~~其实是因为我常数很大。~~

总复杂度可以证明是 \(O((n+q)\log n)\) 的。

Code

超级快读快写啥的这里删掉了，所以直接贺题解会 CE……加上后可以稳定 57pts。

想 AC 的话要卡常。~~我会说我是我自己卡常卡到不让交了让 peterwuyihong 帮我卡常才过的吗？~~

#include <algorithm>
#include <set>
#include <stdio.h>
#include <vector>
typedef long long llt;
typedef unsigned uint;typedef unsigned long long ullt;
typedef bool bol;typedef char chr;typedef void voi;
typedef double dbl;
template<typename T>bol _max(T&a,T b){return(a<b)?a=b,true:false;}
template<typename T>bol _min(T&a,T b){return(b<a)?a=b,true:false;}
template<typename T>T power(T base,T index,T mod){return((index<=1)?(index?base:1):(power(base*base%mod,index>>1,mod)*power(base,index&1,mod)))%mod;}
template<typename T>T lowbit(T n){return n&-n;}
template<typename T>T gcd(T a,T b){return b?gcd(b,a%b):a;}
template<typename T>T lcm(T a,T b){return(a!=0||b!=0)?a/gcd(a,b)*b:(T)0;}
template<typename T>T exgcd(T a,T b,T&x,T&y){if(!b)return y=0,x=1,a;T ans=exgcd(b,a%b,y,x);y-=a/b*x;return ans;}
namespace Splay
{
    struct node
    {
        uint siz;ullt v,max;node*fath,*son[2];
        node(ullt v=0):siz(1),v(v),fath(NULL){son[0]=son[1]=NULL;}
        voi pushup()
        {
            siz=1,max=v;
            if(son[0]!=NULL)siz+=son[0]->siz,_max(max,son[0]->max);
            if(son[1]!=NULL)siz+=son[1]->siz,_max(max,son[1]->max);
        }
        bol howson(){return this==fath->son[1];}
        voi rotate()
        {
            if(fath==NULL)return;
            node*f=fath,*ff=fath->fath;bol sk=howson();
            if((fath=ff)!=NULL)ff->son[f->howson()]=this;
            if((f->son[sk]=son[!sk])!=NULL)son[!sk]->fath=f;
            (son[!sk]=f)->fath=this,f->pushup(),pushup();
        }
    };
    node*rot;
    voi splay(node*p)
    {
        if(p==NULL)return;
        p->pushup();
        while(p->fath!=NULL)
        {
            if(p->fath->fath!=NULL)(p->howson()==p->fath->howson()?p->fath:p)->rotate();
            p->rotate();
        }
        rot=p;
    }
    voi splay2(node*p,node*to)
    {
        if(p==NULL)return;
        p->pushup();
        while(p->fath!=to)
        {
            if(p->fath->fath!=to)(p->howson()==p->fath->howson()?p->fath:p)->rotate();
            p->rotate();
        }
        if(to==NULL)rot=p;
    }
    voi insert(ullt k,ullt v)
    {
        if(rot==NULL){rot=new node(v);return;}
        node*p=rot;
        while(true)
        {
            if(p->son[0]!=NULL)
            {
                if(p->son[0]->siz>k){p=p->son[0];continue;}
                k-=p->son[0]->siz;
            }
            if(k<=1)
            {
            	node*w=new node(v);if((w->son[k]=p->son[k])!=NULL)p->son[k]->fath=w;
            	splay((w->fath=p)->son[k]=w);return;
            }
            k--,p=p->son[1];
        }
    }
    voi kth(ullt k,node*to=NULL)
    {
        node*p=rot;
        while(true)
        {
            if(p->son[0]!=NULL)
            {
                if(p->son[0]->siz>k){p=p->son[0];continue;}
                k-=p->son[0]->siz;
            }
            if(!k){splay2(p,to);return;}
            k--,p=p->son[1];
        }
    }
    voi pre()
    {
        if(rot==NULL||rot->son[0]==NULL)return;
        node*p=rot->son[0];while(p->son[1]!=NULL)p=p->son[1];
        splay(p);
    }
    voi erase(ullt k)
    {
    	kth(k);node*p=rot;
        if(p->son[0]==NULL){if((rot=p->son[1])!=NULL)rot->fath=NULL;}
        else if(p->son[1]!=NULL)pre(),(p->son[1]->fath=rot)->son[1]=p->son[1];
        else(rot=p->son[0])->fath=NULL;
        delete p;splay(rot);
    }
    ullt find(uint l,uint r)
    {
		return kth(l-1),((r==rot->siz)?rot->son[1]->max:(kth(r,rot),rot->son[1]->son[0]->max));
    }
    voi add(uint k,ullt v)
    {
        node*p=rot;
        while(true)
        {
            if(p->son[0]!=NULL)
            {
                if(p->son[0]->siz>k){p=p->son[0];continue;}
                k-=p->son[0]->siz;
            }
            if(!k){p->v+=v,splay(p);return;}
            k--,p=p->son[1];
        }
    }
    // voi add(uint p,ullt v){kth(p),rot->v+=v,rot->pushup();}
};
uint Fath[1000005];
std::set<uint>Leaf;
std::vector<uint>Insert,Erase,Son[1000005];
uint Bgn[1000005],End[1000005],cnt=1,Belong[3000005],Heavy[1000005],Siz[1000005],Up[1000005],Deg[1000005];
ullt A[1000005];
voi get(uint p)
{
	Siz[p]=1,Heavy[p]=-1,Deg[p]=Son[p].size();
	for(auto s:Son[p]){get(s),Siz[p]+=Siz[s];if(Heavy[p]==-1u||Siz[s]>Siz[Heavy[p]])Heavy[p]=s;}
}
voi dfs(uint p,uint user)
{
    Up[Belong[cnt]=p]=user,Splay::insert(cnt,A[Belong[cnt]]),Bgn[p]=cnt++;
    if(~Heavy[p])dfs(Heavy[p],user);
    for(auto s:Son[p])if(s!=Heavy[p])Splay::insert(cnt,0),Belong[cnt++]=p,dfs(s,cnt-1);
    End[p]=cnt;if(Heavy[p]==-1u)Leaf.insert(Bgn[p]);
}
uint read()
{
	uint ans=0;chr c;do c=getchar();while(c>'9'||c<'0');
	do ans=ans*10+c-'0',c=getchar();while(c>='0'&&c<='9');return ans;
}
int main()
{
    uint n,q,op,p;n=read(),q=read();for(uint i=0;i<n;i++)A[i]=read();
    for(uint i=1;i<n;i++)Son[Fath[i]=read()-1].push_back(i);
	get(0),Splay::insert(0,0),dfs(0,0);
    while(q--)
    {
        op=read(),p=read()-1;
        if(op==1)cout<<Splay::find(Bgn[p],End[p])<<endl;
        else
        {
            if(!Splay::find(Bgn[p],End[p]))continue;
            Splay::erase(Bgn[p]),Splay::insert(End[p]-1,0);
            auto iter=Leaf.upper_bound(Bgn[p]);
            while(iter!=Leaf.end()&&*iter<End[p])
            {
            	uint u(Belong[*iter]);uint t(Up[u]);
            	Splay::kth(t);ullt v(Splay::rot->v);
            	Splay::rot->v=0,Splay::add(Bgn[Belong[t]],v);
                if(!Deg[u])
                {
                	Erase.push_back(*iter);
	                if(!--Deg[Fath[u]]||Up[Fath[u]]==t)Insert.push_back(Bgn[Fath[u]]);
                }
                ++iter;
            }
            for(auto s:Erase)Leaf.erase(s);
            for(auto s:Insert)Leaf.insert(s);
            Insert.clear(),Erase.clear();
        }
    }
    return 0;
}

其他思考

整理一下，基于三度化的重构树具有这么几个特性：

是一颗二叉树，结点的儿子被描述成了其所在右链的各个结点的左儿子
右链顶端是实结点，其余为虚结点
除了根节点所在左链，其余左链顶端均虚结点，其它结点为实结点
重构树上的 dfs 序与原树欧拉序对每个非叶结点去掉最后一次出现位置的结果相同
原树上儿子同时把权值贡献给父亲，等价于重构树上儿子向父亲平移权值，再把右链上虚结点权值转移给实结点

我们给出了重构树的概念，至于我们能否用此实现其他功能抑或是建立其他模型，还有待思考。

posted @ 2022-02-14 07:29 myee 阅读(52) 评论(0) 编辑收藏举报

刷新页面返回顶部

myee 的博客

Luogu7952

前言

思路

Code

其他思考

公告