矩阵的定义及基本运算
前言
矩阵在数学和计算机科学中都有非常重要的作用,这篇博客将会向你讲述矩阵的定义及它的基本运算。
一、定义
由 m × n 个数排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。——摘自百度百科
上面这段话很好地定义了矩阵(迷茫.jpg),如果要透彻地理解矩阵的定义,不妨去了解一下矩阵的历史。
为了方便,一般我们都把矩阵封装成一个结构体,贴代码:
1 struct matrix{ 2 int zhen[n][n];//n为矩阵的大小,一般来说,只要不是毒瘤题,直接把数据储存进一个四四方方的矩阵里,是不会爆内存的,也方便我们进行后期的计算 3 void New(){ //初始化 4 for(int i=1;i<=n;i++){ 5 for(int j=1;j<=n;j++){ 6 zhen[i][j]=0; 7 } 8 } 9 } 10 }
二、加(减)法
两个大小为m*n的矩阵A,B相加,则结果矩阵C可以表示为
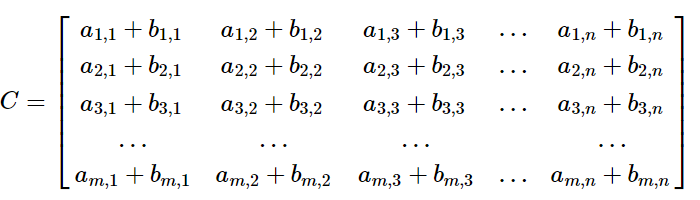
这个部分挺简单的(所以就不贴代码了),就是对应相加,减法其实可以就是加负数。
三、乘法
设A为p*m大小的矩阵,B为n*p大小的矩阵(注意:如果不满足这个条件,则不能相乘),那么相乘结果C的第(i,j)项=$A_{i,1}*B_{1,i}+A_{i,2}*B_{2,i}+A_{i,3}*B_{3,i}+…+A_{i,p}*B_{p,i}$,可以简写为C=AB。
这样说也许有些令人迷惑,但是我们可以从矩阵最初的使用目的来理解。最初,矩阵是用来解线性方程组的。如下面这个方程组:
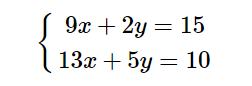
可以表示为:
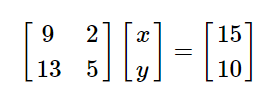
你看,是不是9和x相乘,2和y相相乘,相加等于15,然后,是不是,是不是就变成了方程组中的第一个式子!同样的,下面的式子也是以此类推。
那么接下来就贴代码吧:
matrix mul(matrix a,matrix b){//其实也可以重载运算符的
matrix ans;
ans.New(0);//别忘记初始化
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
ans.zhen[i][j]+=(a.zhen[i][k]*b.zhen[k][j]);//根据定义进行计算
}
}
}
return ans;
}
乘法是矩阵中最重要的基本运算,许多更高级的对矩阵的应用,几乎都是以矩阵乘法为基础的。
矩阵乘法满足乘法结合律,即$(AB)C=A(BC)$。
证明:
设(AB)C=X,A(BC)=Y,B为m*n大小的矩阵。
$X_{i,j}=\sum_{k=1}^{n} (AB)_{i,k}C_{k,j}=\sum_{l=1}^{m}\sum_{k=1}^{n}A_{i,l}B_{l,k}C_{k,j}$
$Y_{i,j}=\sum_{l=1}^{m}A_{i,l}(BC)_{l,j}=\sum_{l=1}^{m}\sum_{k=1}^{n}A_{i,l}B_{l,k}C_{k,j}$
所以,$X_{i,j}=Y_{i,j}$
证毕
要注意的是,矩阵乘法不满足交换律,所以在做题时,要特别注意相乘的顺序。至于证伪,反例其实挺好找的,就不列举出来了。
后言
矩阵作为一种强有力的工具,这篇文章仅仅介绍了基本使用方法,关于矩阵的具体运用,我会在另写一篇博文。
本人水平有限,如果出现错误,欢迎在评论区指正。如果确实帮助到你的话,推荐是对我最大的支持!




