单变量微积分（二）极限和连续

 

 

 

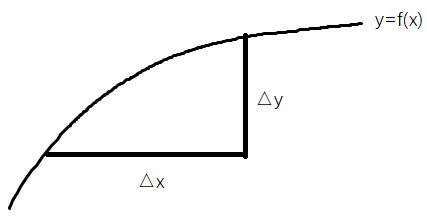
从变化率的角度而言，导数记录了x,y的相对变化率。

因此$\frac{{\Delta y}}{{\Delta x}}$是一种平均变化，取其极限记为 $\frac{{dy}}{{dx}}$ ,这是瞬时变化率。

 

例：

 

1.     q表示电荷， $\frac{{d{\rm{q}}}}{{dt}}$表示电流。

2.     s表示距离， $\frac{{d{\rm{s}}}}{{dt}}$表示速度。

3.     设楼高h=80米，t时刻的h=80-5t²，则t=0,h=80;t=4,h=0.

平均速度 \[\frac{{\Delta h}}{{\Delta t}}{\rm{ = }}\frac{{0{\rm{ - }}80}}{{4{\rm{ - }}0}}{\rm{ =  - }}20\]

瞬时速度$\frac{{d{\rm{h}}}}{{dt}} = 0 - 10t$，当t=4时，h’=-40m/s

4.     T表示温度， $\frac{{dT}}{{dx}}$表示温度梯度。

极限：

$\mathop {\lim }\limits_{{\rm{x}} \to {{\rm{x}}_0}} \frac{{{\rm{f}}\left( {{{\rm{x}}_0} + \Delta {\rm{x}}} \right) - {\rm{f}}\left( {{x_0}} \right)}}{{\Delta {\rm{x}}}}$如果直接代入x=x₀,结果永远是0/0，因此在代入前必须进行一些对消运算。

记：

$\mathop {\lim }\limits_{x \to x_0^ + } f(x)$为右极限， $x \to x_0^ + $b表示x>x₀

同理，$\mathop {\lim }\limits_{x \to x_0^{\rm{ - }}} f(x)$为左极限，$x \to x_0^{\rm{ - }}$表示x<x₀

5：

$$
f(x)=\left\{ \begin{array}{c}
x+1,x>0\\
-x,x\le 0\\
\end{array} \right.
$$

 

 

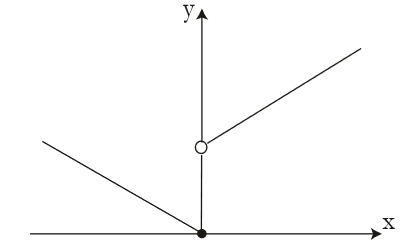
$\mathop {\lim }\limits_{x \to {0^{\rm{ + }}}} f(x) = \mathop {\lim }\limits_{x \to 0} (x + 1) = 1$

$\mathop {\lim }\limits_{x \to {0^{\rm{ - }}}} f(x) = \mathop {\lim }\limits_{x \to 0} ( - x) = 0$

注意这里的左右极限，这里有个小细节：求极限并不需要知道f(0)的值。

连续：

f在x₀点连续，定义为x→x₀时f(x)的极限等于f(x₀)。

这说明：

1.     极限必须存在。

2.     f(x₀)定义。

3.     左极限=右极限。

可去间断点

 

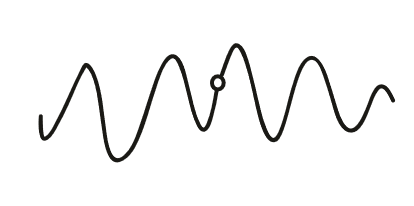
左极限等于右极限，但是不等于f(x₀),或f(x₀)未定义。

跳跃间断点：

 

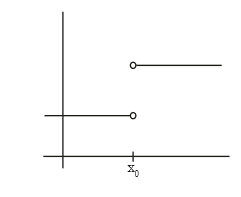
左极限不等于右极限。

无穷间断点：

 

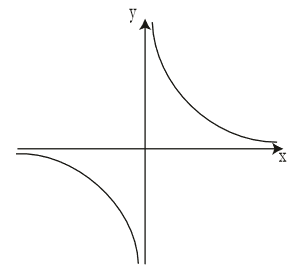
$\mathop {\lim }\limits_{x \to {0^{\rm{ + }}}} \frac{1}{{\rm{x}}} =  + \infty$

$\mathop {\lim }\limits_{x \to {0^{\rm{ - }}}} \frac{1}{{\rm{x}}} = {\rm{ - }}\infty$

其他间断点：

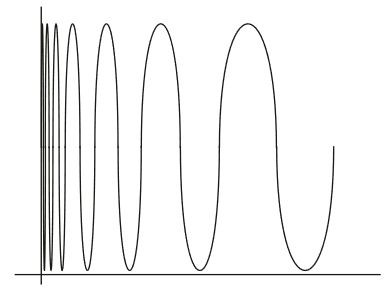
这个函数没有左右极限。

定理：

可导必连续。

如果f在x₀可导，则f在x₀连续

证明：

$\mathop {\lim }\limits_{x \to {{\rm{x}}_0}} f(x) - f({x_0}) = \mathop {\lim }\limits_{x \to {{\rm{x}}_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}(x - {x_0}) = f'({x_0}) \times 0 = 0$

即 $\mathop {\lim }\limits_{x \to {{\rm{x}}_0}} f(x){\rm{ = }}f({x_0})$