单变量微积分（一）导数和变化率

导数的几何解释： 

定义：

F在x₀的导数是y=f(x)在P(x₀,y₀)处的斜率，记为f’(x)。

切线其实是一种极限，是Q趋近于P时，割线PQ的极限。

  

 

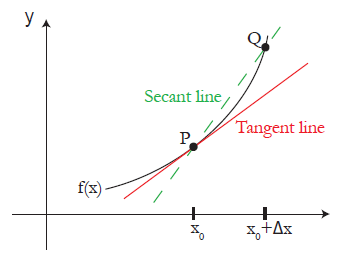
斜率：

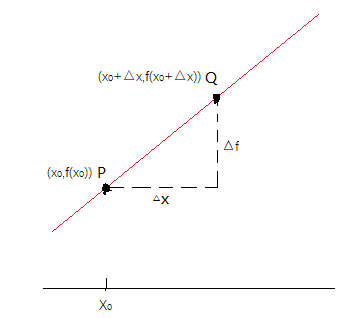
斜率${\rm{m}} = \mathop {\lim }\limits_{\Delta {\rm{x}} \to 0} \frac{{\Delta f}}{{\Delta x}}$

设P为(x₀,f(x₀)),Q(x₀+△x,f(x₀+△x))

则求导公式：

${\rm{f'}}\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta {\rm{x}} \to 0} \frac{{{\rm{f}}\left( {{{\rm{x}}_0} + \Delta {\rm{x}}} \right) - {\rm{f}}\left( {{x_0}} \right)}}{{\Delta {\rm{x}}}}$（一切的根本）

 

例题1：

求导f(x)=  $\frac{1}{x}$。

$\frac{{\Delta f}}{{\Delta x}} = \frac{{\frac{1}{{{x_0} + \Delta x}} - \frac{1}{{{x_0}}}}}{{\Delta x}}$（学名：差商）

化简后

$\frac{\Delta f}{\Delta x}=\frac{-1}{(x_0+\Delta x)x_0}\mathop {\rightarrow} \limits_{\Delta x\rightarrow 0}\frac{-1}{x_{0}^{2}}$

因此，    ${\rm{f'}}\left( {{x_0}} \right) = \frac{{ - 1}}{{x_0^2}}$

例题2：

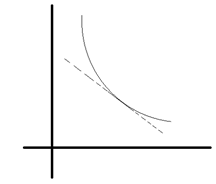
求由y=  $\frac{1}{x}$切线和坐标轴围合而成的三角形区域面积，如图：

由例1，可以得到切线方程为  ${\rm{y - }}{y_0} =  - \frac{1}{{x_0^2}}(x - {x_0})$

设y=0,则  $0{\rm{ - }}\frac{1}{{{{\rm{x}}_{\rm{0}}}}} =  - \frac{1}{{x_0^2}}(x - {x_0})$，化简得  ${\rm{x}} = 2{x_0}$

同理，y轴截距为

所以三角形面积为：

 $S{\rm{ = }}\frac{1}{2}(2{x_0})(2{y_0}) = 2{x_0}{y_0} = 2$

一些记号：

 ${\rm{f' = }}\frac{{df}}{{dx}} = \frac{{dy}}{{dx}}$

例题3：

${\rm{f}}(x) = {x^n}$，n=1,2,3…，求f’(x)。

首先$\frac{{\Delta {\rm{f}}}}{{\Delta x}}{\rm{ = }}\frac{{{{(x + \Delta x)}^n} - {x^n}}}{{\Delta x}}$ ，其中由二项式定理  ${(x + \Delta x)^n}{\rm{ = }}{{\rm{x}}^{\rm{n}}} + n{x^{n - 1}}\Delta x + {\rm O}{(\Delta x)^2}$

则  $\frac{{\Delta {\rm{f}}}}{{\Delta x}}{\rm{ = }}\frac{1}{{\Delta x}}({x^n} + n{x^{n - 1}}\Delta x + {\rm O}({(\Delta x)^2}) - {x^n}) = n{x^{n - 1}} + {\rm O}({(\Delta x)^2})$

因此  ${\rm{f'(x) = }}n{x^{n - 1}}$