相机-imu外参校准总结

1. 研究背景及相关工作

1)研究背景

       单目视觉惯性slam是一种旨在跟踪移动平台的增量运动并使用来自单个车载摄像头和imu传感器的测量结果同时构建周围环境地图的技术。视觉相机和惯性测量单元(imu)是slam技术的理想选择，因为这两种传感器模式尺寸小，价格便宜，功耗低，并且可以相互补充。视觉传感器在大多数纹理丰富的场景中效果很好，但是如果遇到玻璃，白墙等特征较少的场景，基本上无法工作；imu长时间使用有很大的累计误差，但在短时间内，其相对位移数据又有很高的精度。所以视觉传感器失效时，融合imu数据，能够提高定位的精度，并且在系统正常运行过程中结合相机和imu数据同时对状态进行估计。这些属性使得视觉惯性组合可以广泛用于实际应用中，例如机器人导航[1][2]，自动或半自动驾驶[3]，实时三维重建[4]，虚拟和增强现实[5]。

　　几种视觉惯性融合技术已经被提出，像递归(卡尔曼滤波)算法[6][7]，使用imu测量数据进行状态积分，以及基于关键帧的非线性优化方法[8][9][10]，同时最小化视觉和惯性几何误差。然而这些方法的性能很大程度上取决于相机和imu之间的6自由度的精确外部参数校准。无论是在求取相机位姿的时候还是在后端融合相机和imu数据进行状态优化的过程中都用到了外部参数。不正确的校准将在运动估计中引入系统偏差并降低整体导航性能。

2)相关工作

　　获得精确外部参数的一种代替方法是利用离线方法[11][12][13]。然而，这些方法复杂且耗时，因为他们通常需要专业人士小心地将传感器套件移动到固定的校准目标前面。此外，每当重新定位传感器或施加显著的器械应力时，通常需要重复该过程。另一种替代方案是应用在线校准方法来联合估计初始值和外部参数。Kelly等人提出了一种基于无迹卡尔曼滤波器的自校准方法[14]来校准外部参数。Martinelli引入了一种封闭形式的解决方案来估计初始值[15]，后来在[16]中提出了它的修订，以自动估计陀螺仪偏差。Yang和Shen用基于优化的线性估计器校准外部参数和初始值(imu偏差除外)[17]。在他们的扩展单目视觉惯性系统(VINS-Mono)中，imu偏差校准包含在滑动窗口非线性估计器中[18]。

2. 问题描述

　　因为优化时，拥有视觉和惯性两种传感器数据，需要利用这两种数据同时对系统状态进行优化。所以，我们认定以imu位姿为基准，在进行图像点与空间点的操作时便通过桥梁—外参R和T将imu位姿转换成相机位姿。所以R T的精准度极为重要。

　　　　　　

 

3. 本人问题的描述及解决办法

输入：Ps[i] Rs[i] 图像帧 (Ps Rs 代表imu位姿，精度极高)

输出：R T(相机-imu外参)

• 根据公式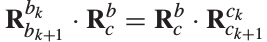,求出R的初值，这里用到了相机位姿，所以需要做纯视觉初始化。
• 需要求尺度s，公式如下。这里需要做改进，因为T未知，所以同时将T设为待求量(改进公式见笔记本)。 (求出s后还可以通过该公式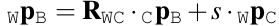求出T的初值 )
  

　　　　　　

• 第三步非线性优化时会优化空间点深度，所以这步要做三角化，初始化深度。(三角化时，以相邻两帧的相机位姿为基准，所以会用到纯视觉初始化的相机位姿)。
• 非线性紧耦合优化，公式：

                     

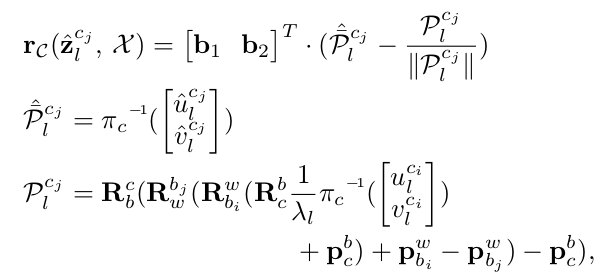
          同时优化R T和空间点深度λ。

4. 新思路

1)    简单对比发现vi orb-slam的初始化考虑因素更多一些(包括求取了加速度偏置，以及外参的平移)，两个方法的初始化详细对比见我的另一篇博客https://www.cnblogs.com/mybrave/p/9564899.html。

　　所以，尝试做该实验，将vi orb-slam中视觉惯导初始化的部分移植到vins中，查看优化效果。

2)

• 使用双目相机算出R的初值。
• 直接通过双目算出空间点深度，这里便不需要求s和相机平移。
• 第三步进行非线性紧耦合优化公式为：

　　　　　　

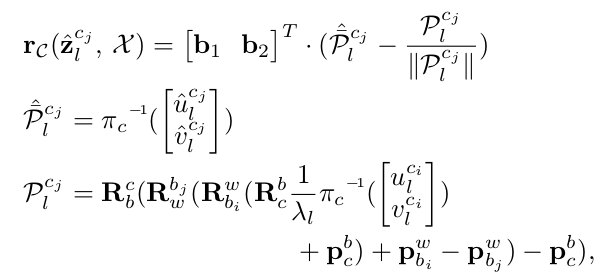
　　(双目求出的空间点深度要比单目+imu算出的深度更精确吗？？？ 差别就在尺度s和两帧之间的旋转平移的准确度上，尺度s即在初始化的过程中求出)

 

 

 

 

 

[1] A. Stelzer, H. Hirschmüller, and M. Görner, “Stereo-vision-based navigation of a six-legged walking robot in unknown rough terrain,” Int. J. Robot. Res., vol. 31, no. 4, pp. 381–402, 2012.
[2] H. Liu, Z. Wang, and P. Chen, “Feature points selection with flocks of features constraint for visual simultaneous localization and mapping,” Int. J. Adv. Robot. Syst., vol. 14, no. 1, pp. 1–11, 2016.

[3] S. Weiss, D. Scaramuzza, and R. Siegwart, “Monocular-SLAM-based navigation for autonomous micro helicopters in GPS-denied environments,” J. Field Robot., vol. 28, no. 6, pp. 854–874, 2011.

[4] P. Tanskanen, K. Kolev, L. Meier, F. Camposeco, O. Saurer, and M. Pollefeys, “Live metric 3d reconstruction on mobile phones,” in Proc. IEEE Int. Conf. Comput. Vision, 2013, pp. 65–72.

[5] T. Oskiper, S. Samarasekera, and R. Kumar, “Multi-sensor navigation algorithm using monocular camera, IMU and GPS for large scale augmented reality,” in Proc. IEEE Int. Symp. Mixed Augmented Reality, 2012, pp. 71–80.

[6] M. Li and A. I. Mourikis, “Improving the accuracy of EKF-based visual-inertial odometry,” in Proc. IEEE Int. Conf. Robot. Autom., 2012, pp. 828–835.
[7] P. Tanskanen, T. Naegeli, M. Pollefeys, and O. Hilliges, “Semi-direct EKF-based monocular visual-inertial odometry,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2015, pp. 6073–6078.
[8] S. Leutenegger, S. Lynen, M. Bosse, R. Siegwart, and P. Furgale, “Keyframe-based visual-inertial odometry using nonlinear optimization,” Int. J. Robot. Res., vol. 34, no. 3, pp. 314–334, 2015.

[9] V. Usenko, J. Engel, J. Stückler, and D. Cremers, “Direct visual-inertial odometry with stereo cameras,” in Proc. IEEE Int. Conf. Robot. Autom., 2016, pp. 1885–1892.
[10] C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “IMU preintegration on manifold for efficient visual-inertial maximum-a-posteriori estimation,” in Proc. Robot. Sci. Syst., 2015.
[11] J. Rehder and R. Siegwart, “Camera/IMU calibration revisited,” IEEE Sensors J., vol. 17, no. 11, pp. 3257–3268, 2017.
[12] P. Furgale, J. Rehder, and R. Siegwart, “Unified temporal and spatial calibration for multi-sensor systems,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2013, pp. 1280–1286.
[13] P. Furgale, T. D. Barfoot, and G. Sibley, “Continuous-time batch estimation using temporal basis functions,” in Proc. IEEE Int. Conf. Robot. Autom., 2012, pp. 2088–2095.
[14] J. Kelly and G. S. Sukhatme, “Visual-inertial sensor fusion: Local-ization, mapping and sensor-to-sensor self-calibration,” Int. J. Robot. Res., vol. 30, no. 1, pp. 56–79, 2011.
[15] A. Martinelli, “Closed-form solution of visual-inertial structure from motion,” Int. J. Comput. Vision, vol. 106, no. 2, pp. 138–152, 2014.
[16] J. Kaiser, A. Martinelli, F. Fontana, and S. Scaramuzza, “Simultaneous state initialization and gyroscope bias calibration in visual inertial aided navigation,” IEEE Robot. Autom. Lett., vol. 2, no. 1, pp. 18–25,
2017.

[17] Z. Yang and S. Shen, “Monocular visual-inertial state estimation with online initialization and camera-IMU extrinsic calibration,” IEEE Trans. Autom. Sci. Eng., vol. 14, no. 1, pp. 39–51, 2017.

[18] Y. Lin, F. Gao, T. Qin, W. Gao, T. Liu, W. Wu, Z. Yang, and S. Shen, “Autonomous aerial navigation using monocular visual-inertial fusion,” J. Field Robot., 2017.