光流法学习

 

光流的计算

 

光流估计就是指利用时间上相邻的两帧图像，得到点的运动。满足以下几点假设：

• 前后两帧点的位移不大（泰勒展开）
• 外界光强保持恒定。
• 空间相关性，每个点的运动和他们的邻居相似（连续函数，泰勒展开）

在相邻的两帧图像中，点(x,y)发生了位移(u,v)，那么移动前后两点的亮度应该是相等的。如下：

                                            

从这个式子出发，我们将其利用Taylor展开做一阶线性近似。其中Ix, Iy, It分别是Image对这几个变量的偏导数。

                           

上面两式联立，可以得到，

　　　　　　　                       　

上式中，可以通过图像沿xx方向和yy方向的导数计算，可以通过计算。未知数是， 正是我们想要求解的每个像素在前后相邻两帧的位移。

 

上面就是光流估计的基本思想。上述式子虽然给出了光流估计的思路，但是还是没有办法解出位移量。

 

L-K方法

 

Lucas-Kanade方法是一种具体的求解方法。L-K方法依据相邻像素之间的位移相似的假设，通过一个观察窗口，将窗口内的像素点的位移看做是相同的，建立了一个超定方程，使用最小二乘法进行求解。下面是观察窗口为5×5的时候，建立的方程。

                          

 

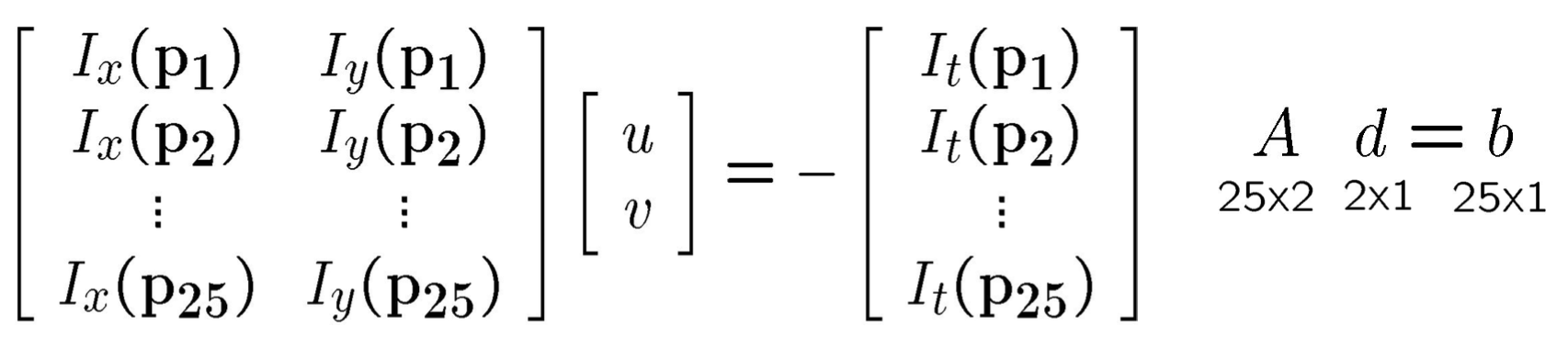
使用最小二乘法求解，可以得到如下的式子，求和号代表是对窗口内的每一个像素点求和。        

                         

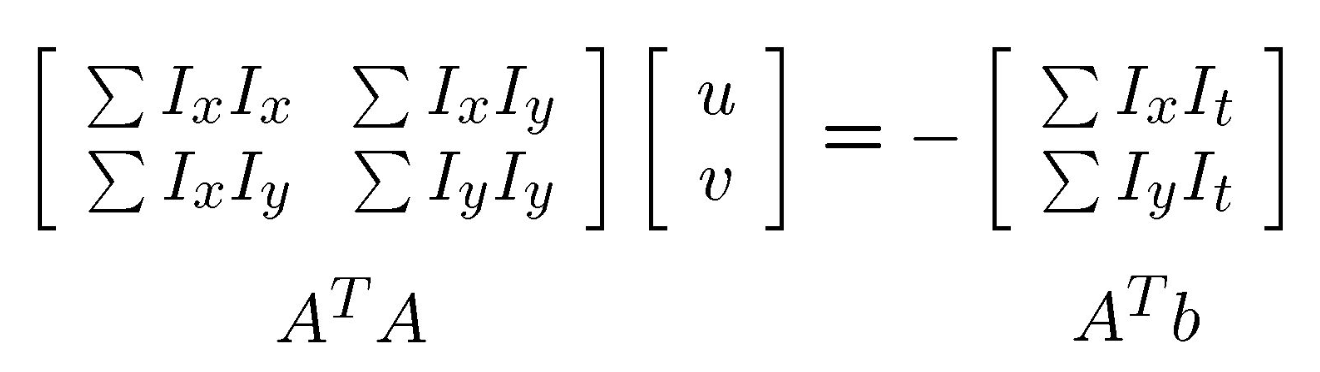
上式即是L-K方法求解光流估计问题的方程。

 

金字塔方法

 在最开始的假设中，第一条指出点的位移应该是较小的。从上面的分析可以看出，当位移较大时，Taylor展开式一阶近似误差较大。其修正方法就是这里要介绍的金字塔方法。我们通过将图像降采样，就能够使得较大的位移在高层金字塔图像中变小，满足假设条件1.如下所示。

                              

 

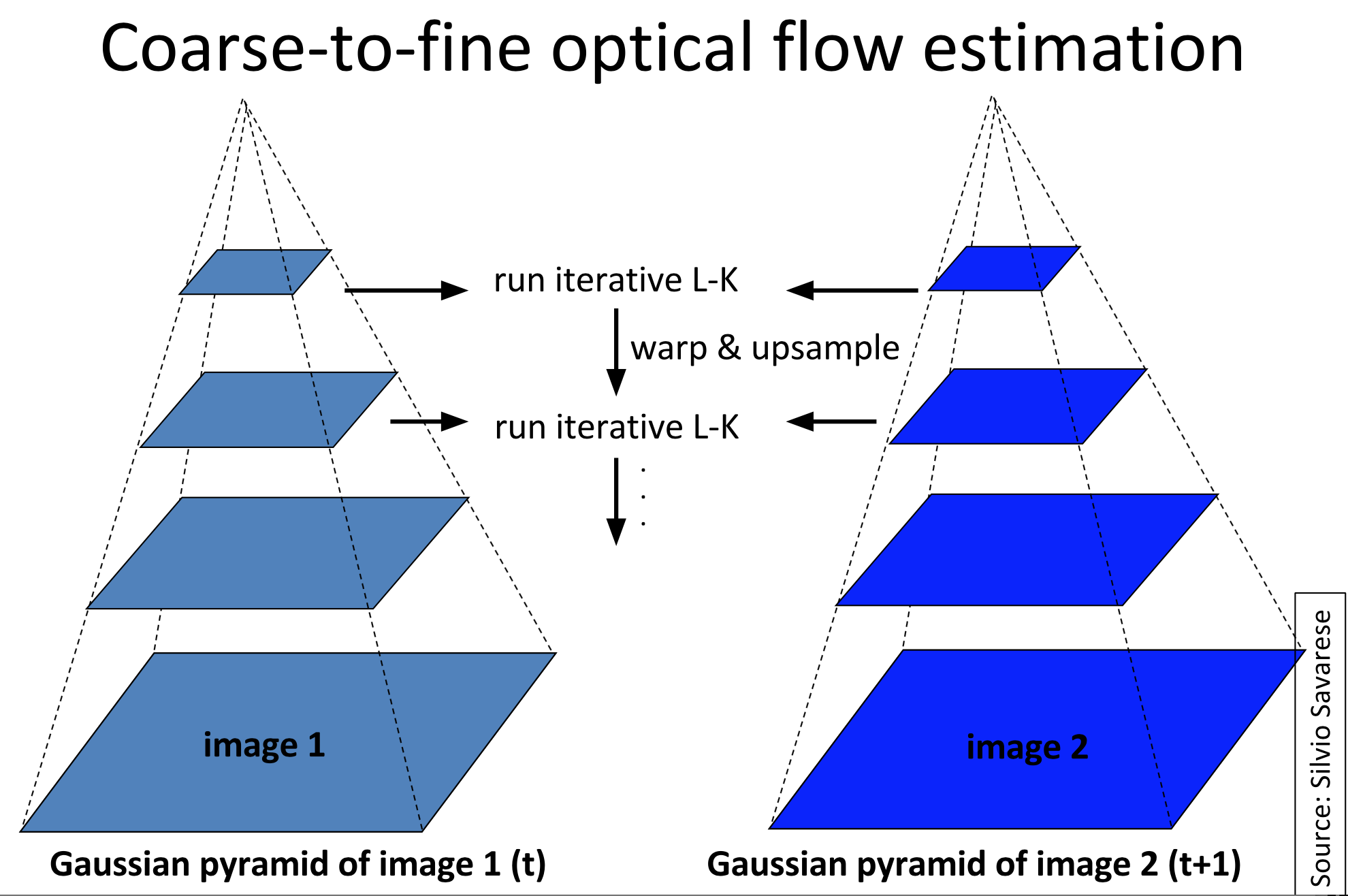
求像素梯度

而图像是一个二维函数f(x,y)，其微分当然就是偏微分。因此有：

　                    　

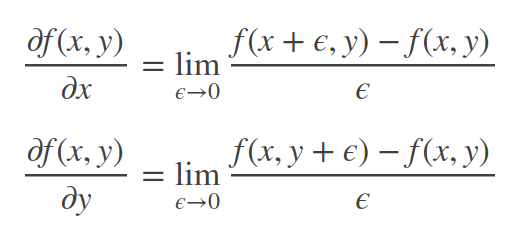
因为图像是一个离散的二维函数，ϵ不能无限小，我们的图像是按照像素来离散的，最小的ϵ就是1像素。因此，上面的图像微分又变成了如下的形式（ϵ=1）：

                          

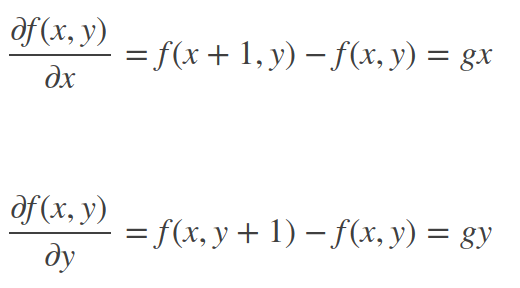
这分别是图像在(x, y)点处x方向和y方向上的梯度，从上面的表达式可以看出来，图像的梯度相当于2个相邻像素之间的差值。

 

梯度的方向是函数f(x,y)变化最快的方向，当图像中存在边缘时，一定有较大的梯度值，相反，当图像中有比较平滑的部分时，灰度值变化较小，则相应的梯度也较小，图像处理中把梯度的模简称为梯度，由图像梯度构成的图像成为梯度图像(we can get the gradient image through computing the gradient of each pixel in the image)
经典的图像梯度算法是考虑图像的每个像素的某个邻域内的灰度变化，利用边缘临近的一阶或二阶导数变化规律，对原始图像中像素某个邻域设置梯度算子，通常我们用小区域模板进行卷积来计算，有Sobel算子、Scharr 算子(opencv)、Robinson算子、Laplace算子等。

 

Opencv求光流函数　　　

函数位置opencv-2.4.9/modules/video/src/lkpyramid.cpp

void cvCalcOpticalFlowPyrLK(
                            const CvArr* prev,
                            const CvArr* curr,
                            CvArr* prevPyr,
                            CvArr* currPyr,
                            const CvPoint2D32f* prevFeatures,
                            CvPoint2D32f* currFeatures,
                            int count,
                            CvSize winSize,
                            int level,
                            char* status,
                            float* track error,
                            CvTermCriteria criteria,
                            int flags );

 

  

1. 光流估计 https://xmfbit.github.io/2017/05/03/cs131-opticalflow/ 

2. 图像梯度的基本原理 https://blog.csdn.net/saltriver/article/details/78987096

3. 数字图像的梯度概念以及计算(the gradient of the image) https://blog.csdn.net/computer_liuyun/article/details/21328753

4. opencv入门12:梯度和边缘检测-GRADIENTS AND EDGE DETECTION https://harveyyeung.github.io/2018/05/11/PracPythonOpenCV/PracPythonOpenCV12/#espandi

5. Lucas-Kanade算法原理介绍及OpenCV代码实现分析  https://blog.csdn.net/banyao2006/article/details/39484113#commentBox

6. [learning opencv]第十章 跟踪与运动：金字塔Lucas-kanade(cvCalcOpticalFlowPyrLK)检测光流  https://blog.csdn.net/moc062066/article/details/6636106