链表中环的的入口节点

题目：给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

题解：

1. 方法一：哈希法

   1. 遍历单链表的每个结点
   2. 如果当前结点地址没有出现在set中，则存入set中
   3. 如果当前节点出现在set中，则当前结点就是环的入口结点
   4. 整个单链表遍历完，若没出现在set中，则不存在环

   时间复杂度：O(N)O(N)，其中 NN 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。

   空间复杂度：O(N)O(N)，其中 NN 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。

 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}

import java.util.*;
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead)
    {
       Set<ListNode> set = new HashSet();
        while(pHead != null){
            if(set.contains(pHead)){
                return  pHead;
            }
            set.add(pHead);
            pHead = pHead.next;
        }
        return null; 
    }
}

2. 方法二：快慢指针

我们使用两个指针，fastNode 与slowNode。它们起始都位于链表的头部。随后，slowNode指针每次向后移动一个位置，而fastNode 指针向后移动两个位置。如果链表中存在环，则 fastNode 指针最终将再次与slowNode 指针在环中相遇，如果不存在环，那么fastNode率先到达链表末尾。

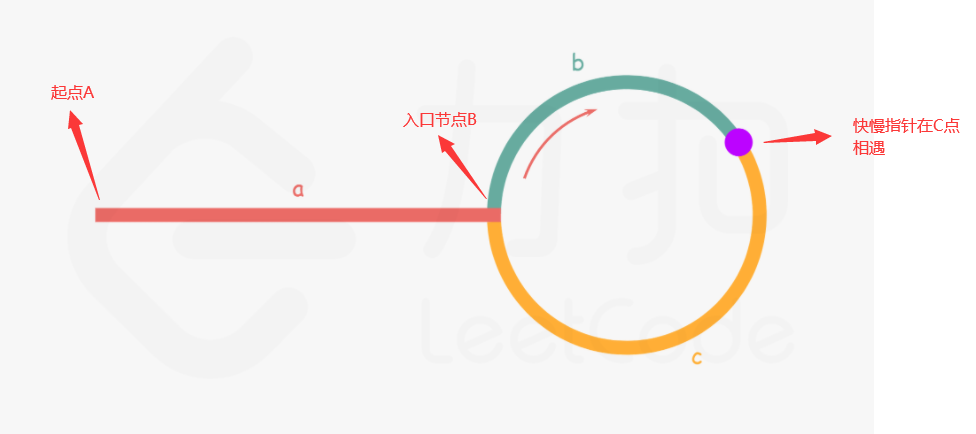
假设链表中存在环，由于fastNode指针每次都比slowNode指针多走一步，所以fastNode会率先进入到环中，当slowNode也进入到环中时，由于快fastNode和slowNode速度的差异，fastNode最终会追上slowNode，假设在C点相遇，因为快指针是慢指针速度的两倍，由此可以列出等式2(a+b)=a+(n+1)b+nc ---->a=(n-1)b +nc 其中n为fastNode指针在环中走的第几圈,我们会发现从相遇点到入环点的距离(c)加上 n−1 圈的环长(b+c)，恰好等于从链表头部到入环点的距离。所以，当快慢指针第一次在C点相遇时，我们额外使用一个指针p从起点出发，p指针和slowNode指针最终会在入口节点B相遇

 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead)
    {
        ListNode fastNode = pHead;
        ListNode slowNode = pHead;
        while(fastNode != null){
            slowNode = slowNode.next;
            fastNode = fastNode.next;
            // 快指针走到链表末尾
            if(fastNode == null){
                return null;
            }
            //快指针走两步
            fastNode = fastNode.next;
            //fastNode == slowNode则快慢指针在环中相遇
            if(fastNode == slowNode){
                ListNode p = pHead;
                while(p != slowNode){
                    p = p.next;
                    slowNode = slowNode.next;
                }
                return p;
            }
        }
        return null;
    }
}