神经网络由各个部分组成
1.得分函数:在进行输出时,对于每一个类别都会输入一个得分值,使用这些得分值可以用来构造出每一个类别的概率值,也可以使用softmax构造类别的概率值,从而构造出loss值, 得分函数表示最后一层的输出结果,得分函数的维度对应着样本的个数和标签的类别数

得分结果的实例说明:一个输入样本的特征值Xi 1*4, w表示权重参数3*4,这里使用的是全连接y = w * x.T,输出结果为3*1, 这3个结果分别表示3种标签的得分值
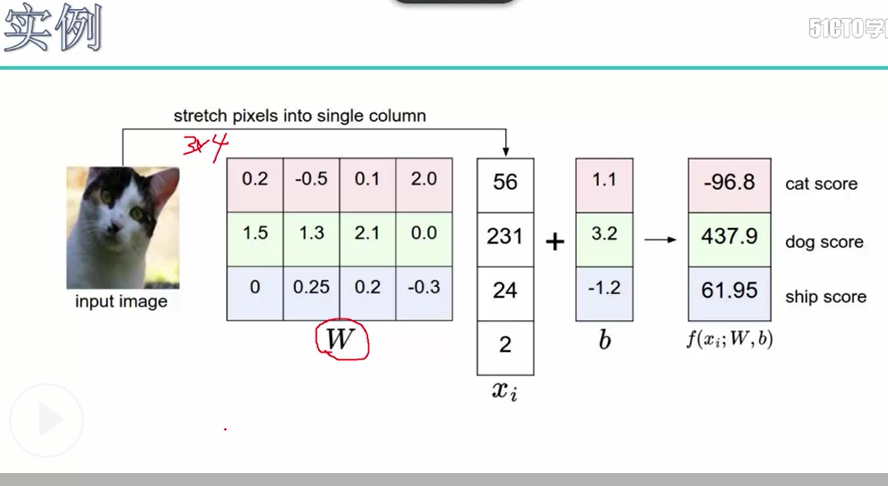
代码说明:
out = np.dot(x_row, w) + b # (N,M) 即 f = x.*w + b
2.损失函数:表示的是根据得分值计算出实际标签得分与其他类别得分的差异值,称为损失函数
SVM损失函数:Li = ∑ max(0, sj - syi + 1) sj表示其他类别得分值, syi表示真实类别的得分值, 1表示真实得分与其他类别得分该有的差异值

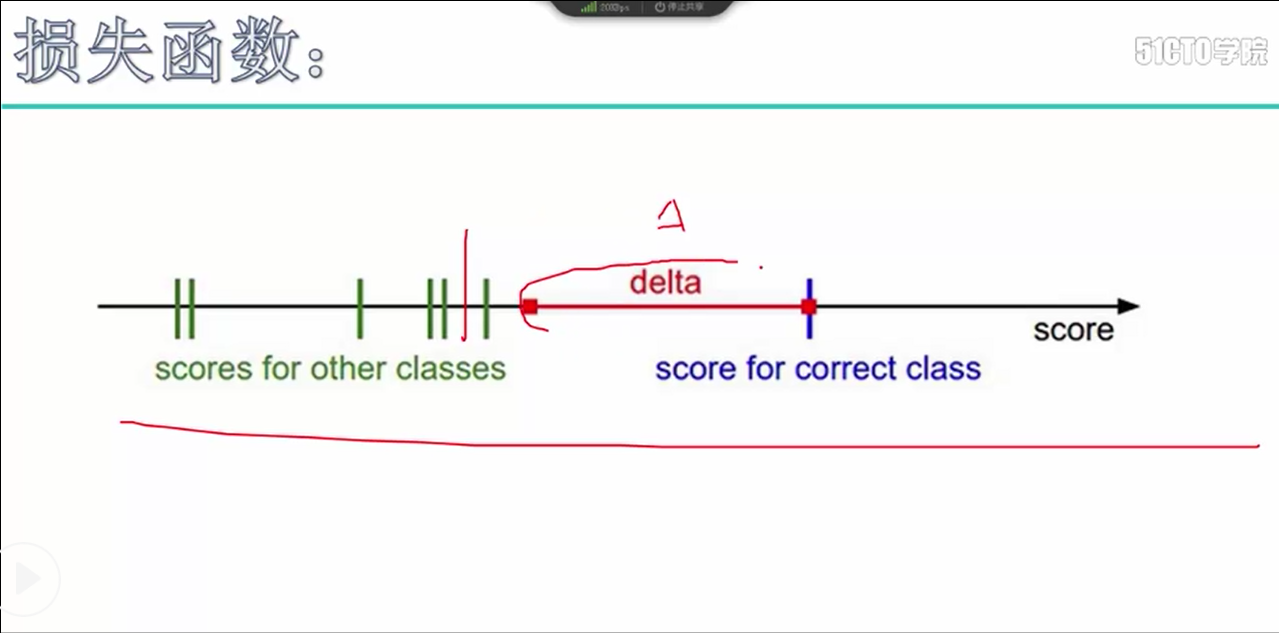
delta表示真实得分与其他类别得分该有的差异值
这是一个样本所获得的损失值,我们需要对所有的样本计算损失值,对损失值进行加和,为了避免样本数量的干扰,除以N

3.正则化惩罚项:就是将对应的权重参数进行加和,
对于L1权重参数:np.sum(abs(w))
对于L2权重参数:0.5 * np.sum(w * w)
举例说明:我们可以看出np.dot(x, w.T) 的结果:w1和w2是一样的,但是我们可以明显看出w2比w1的参数要更好一些,因为w1参数在1号位置上有权重,在其他位置上都为0,因此容易发生过拟合的现象,而w2要显得更加的平均,我们在加入L2惩罚项进行计算,w1的惩罚项是1, w2的惩罚项是0.25,因此w2显得要更好一些
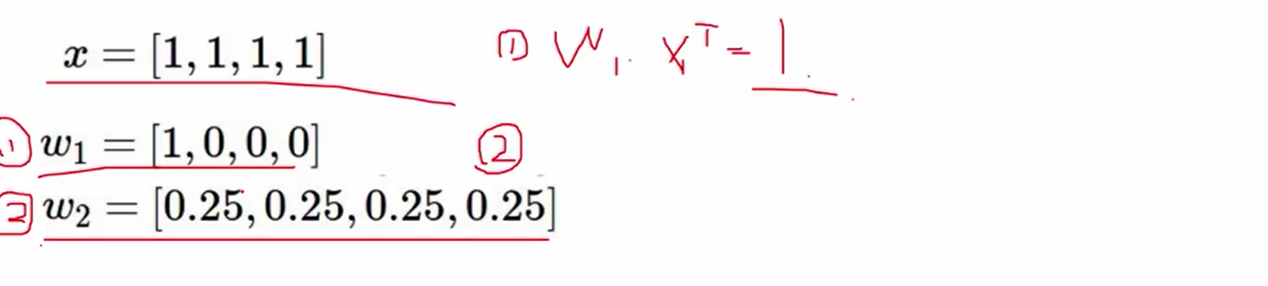
代码说明: L2惩罚项加和, 即为W1参数的加和项
reg_loss = 0.5 * self.reg * np.sum(W1*W1) + 0.5 * self.reg * np.sum(W2*W2)
4. softmax分类器
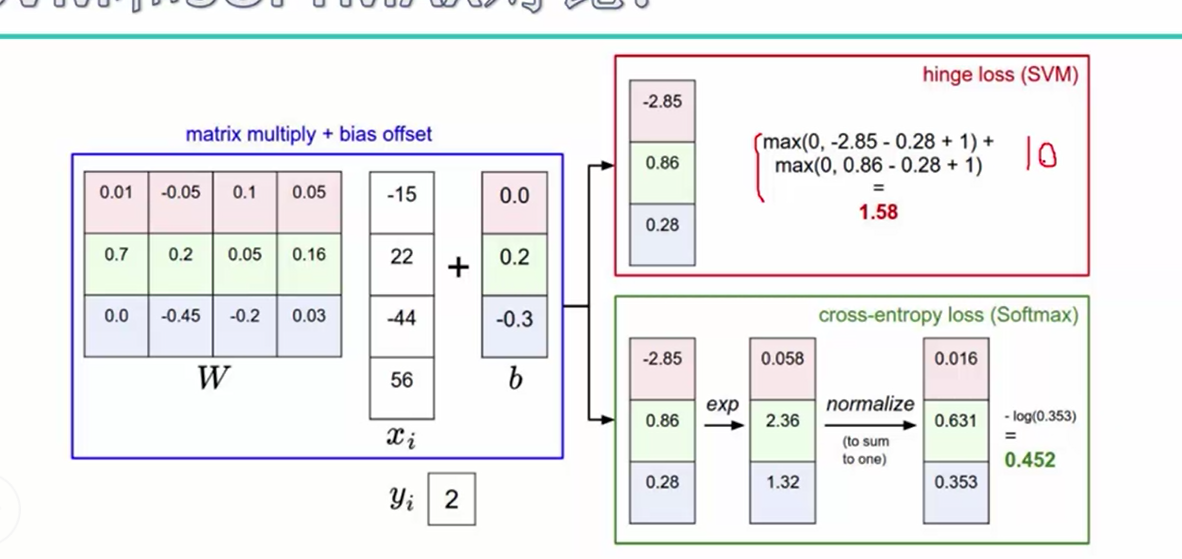
使用的概率值为:-log(e^fyj / ∑e^fyi) e^fyj表示e^类别的得分值, ∑e^fyi表示所有类别的得分值之和,相当于对得分做了一个归一化的操作
实例说明:我们可以看出进行归一化后的概率明显要小很多, 这也成为交叉熵损失函数

代码说明:对于每一个样本,只选取真实标签的概率值,并将最后的结果进行加和,除以N作为损失值
probs = np.exp(x - np.max(x, axis=1, keepdims=True))
probs /= np.sum(probs, axis=1, keepdims=True)
N = x.shape[0]
loss = -np.sum(np.log(probs[np.arange(N), y])) / N
使用两种损失函数做对比,假设真实得分为10,其他类别得分为9,对于svm的损失值为0,而对于softmax的损失值不为0,因此可以称之为一种不容易满意的损失函数
5. 最优化问题
最优化问题:表示的是我们如何选择参数w,使得损失函数J(Θ)可以最快达到最小,这里使用的是dJ(Θ)/ dΘ即使用参数对损失函数进行求导操作

在进行神经网络的求解过程中,主要是分为两个步骤,一个是前向传播,用于计算scores得分与损失函数loss

代码:前向传播的代码
# 权重参数w和b W1, b1 = self.params['W1'], self.params['b1'] W2, b2 = self.params['W2'], self.params['b2'] # 第一层的输出结果 h1, cache1 = affine_relu_forward(X, W1, b1) # 第二层的输入结果 out, cache2 = affine_forward(h1, W2, b2) scores = out # (N,C) # 如果没有labels,直接返回得分值作为预测结果 if y is None: return scores # 计算损失值和softmax的反向传播的结果 loss, grads = 0, {} data_loss, dscores = softmax_loss(scores, y)
6. batch_size 表示在训练过程中,每次只是用部分数据进行参数的更新操作
代码说明:
# 构造随机序号, 用于进行训练样本的抽取 batch_mask = np.random.choice(num_train, self.batch_size) # 获得训练图片和对应的标签值 X_batch = self.X_train[batch_mask] y_batch = self.y_train[batch_mask] # 使用bacth_size计算梯度值和更新的参数, grads表示参数的梯度值 loss, grads = self.model.loss(X_batch, y_batch) self.loss_history.append(loss)
7.反向传播,用于进行参数的更新操作即dw1, dw2, db1和db2

这里对于softmax的反向传播做一个参数的说明:
softmax的反向传播:d(-log(e^x - a)/ ∑e^x) / dx = (σ(x) - 1) / N
dx[np.arange(N), y] -= 1
dx /= N
第二层反向传播x * w.T + b :dx, dw, db = dout * w.T, dout.T * x, np.sum(dout, axis=0) , (x, w, b)表示当前层的输入值,
(x, w, b) = cache # 当前层的输入 dx, dw, db = None, None, None dx = np.dot(dout, w.T) # 获得dx的结果,用于上一层的反向传播 dx = np.reshape(dx, x.shape) # 为了与输入x保持一样的维度 x_row = x.reshape(x.shape[0], -1) dw = np.dot(x_row.T, dout) # dj(Θ)/dw = dj(Θ)/dy * dy/dw = dout * x 链式法则 db = np.sum(dout, axis=0, keepdims=True) # dj(Θ)/db = dj(Θ)/dy * dy/db = dout * 1 = dout
第一层反向传播relu层:np.maximum(0, x) 的反向传播, 当x>0时,反向传播的结果为本身,输入x<0,反向传播的结果为0
x = cache # cache表示relu的输入x dout[x < 0] = 0 # 对于输入x小于0的反向传播的结果也是等于0
第一层反向传播x*w.T+b, 与第二层的反向传播的过程时相同的
(x, w, b) = cache # 当前层的输入 dx, dw, db = None, None, None dx = np.dot(dout, w.T) # 获得dx的结果,用于上一层的反向传播 dx = np.reshape(dx, x.shape) # 为了与输入x保持一样的维度 x_row = x.reshape(x.shape[0], -1) dw = np.dot(x_row.T, dout) # dj(Θ)/dw = dj(Θ)/dy * dy/dw = dout * x 链式法则 db = np.sum(dout, axis=0, keepdims=True) # dj(Θ)/db = dj(Θ)/dy * dy/db = dout * 1 = dout



 浙公网安备 33010602011771号
浙公网安备 33010602011771号