动态规划

动态规划(基本上都需要开一个数组来进行记录数据)

是什么？

动态规划（dynamic programming）是运筹学的一个分支，是求解决策过程（decision process）最优化的数学方法。动态规划一般可分为线性动规，区域动规，树形动规，背包动规四类。

①线性动规：拦截导弹，合唱队形，挖地雷，建学校，剑客决斗等；

②区域动规：石子合并，加分二叉树，统计单词个数，炮兵布阵等；

③树形动规：贪吃的九头龙，二分查找书，聚会的欢乐，数字三角形等；

④背包问题：01背包问题，完全背包问题，分组背包问题，二维背包，装箱问题，挤牛奶等；

基本思路？

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

即动态规划的核心思想是把原问题分解成子问题进行求解，也就是分治的思想。(大事化小，小事化了)但是相比于分治算法，动态规划能避免大量的重复计算

什么问题适合使用动态规划？

求问题的最值情况、求这个问题有多少种求解方法、最优解的情况、存在问题(判断能否能够做到问题)和具有重叠子问题等 

解决动态规划的步骤？

①划分状态(确定状态)，即划分子问题。

　　确定最后一步，即最后一步的前一步肯定也是最优的解。(确定最后一步，来往前推一步，便于得到子问题的方程式子) 

　　子问题，即找出于原问题解决方法一样但问题规模减小。找出递归式子 。但是递归会具有计算许多的重复项，则我们需要将计算结果保存下来，并改变计算顺序。

②状态转移(转移方程)，即如何让计算机理解子问题，将子问题求解的递归方程表示出来。

③初始条件和边界情况，确定初始状态是什么？最小的子问题？最终状态又是什么。(一般的初始条件是F[0]=0)

④ 计算顺序，确定是从头开始还是从尾开始计算。(对于一维数组一般情况是从小到大，而二维数组一般是从左到右，从上到下的顺序。这里的数组一般是用来进行保存记录先前算出的值。即就是当我们要计算一个值时，若从头到尾计算，计算这个值所需的值已经计算过了，则是从头到尾的顺序。否则相反)

动态规划的举例？

例子1：Coin change

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)

Example 2:
coins = [2], amount = 3
return -1.

中文：给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。你可以认为每种硬币的数量是无限的。

先计算具有2、5、7这三种硬币，需要凑出27元钱的具体例子，随后再求出其他用户设定的情况。

思路：

（1）首先我们根据题意可以知道我们的子问题情况，即先假设要凑x元，F[x]：表示该凑x元(amount)需要最少硬币的硬币数量。则可以将原问题进行用符号表示，即凑27元：F[27]表示。F[27]表示的为最后一步凑出27元。则它的前一步有三种情况：①用2元硬币来凑 ②用3元硬币来凑 ③用4元硬币来凑,最后在从这三种情况中选出最小的一种，即为用最少硬币凑出27元

① F[27]=F[27-2]+1，其中加1表示从25元到27元只需要1步　　　　② F[27]=F[27-5]+1 　　　　③F[27]=F[27-7]+1

（2）其次是其中三种情况中又存在F[25]、F[22]和F[20]的求解情况。而F[25]、F[22]和F[20]的求解又满足于上述（1）的步骤，类似于求解子问题。

因而子问题的公式为F[x]=min{F[x-2]+1,F[x-5]+1,F[x-7]+1}

（3）函数初始化：当凑0元时，则一块硬币也不需要，即F[0]=0。而x的边界为x<=27

 

a=int(input()) //表示需要凑的那个数x
b=[]  //用来存储硬币的种类
for i in input().split(' '):
    b.append(eval(i))
f=[0]*(a+1) //开辟一个数组，用来记录每次凑钱需要最小的硬币数量
f[0]=0 //初始条件，当要凑出0元钱，不需要硬币数量
for j in range(1,a+1): //将凑出来1、2、3、......a元所需的最小硬币数量表示出来
    f[j]=float('inf') //将不能用零钱凑出来的钱用无穷大来表示
    for k in b: //表示求解式子：F[x]=min{F[x-2]+1,F[x-5]+1,F[x-7]+1}
        if (j-k)>=0 and f[j-k]!=float('inf'): //(j-k)>=0表示为该钱可以用被len(b)种硬币表示出来，不然带入式子F[x]=min{F[x-2]+1,F[x-5]+1,F[x-7]+1}求解胡出现x<0,这种情况不存在；而f[j-k]!=float('inf')表示为这个钱能用硬币凑出来。
              num=f[j-k]+1 //表示f[j]=f[j-k]+1
              if num<f[j]: 
                  f[j]=num //每次将最优的情况记录下来
print(f[a])

 

例子2：Unique Paths

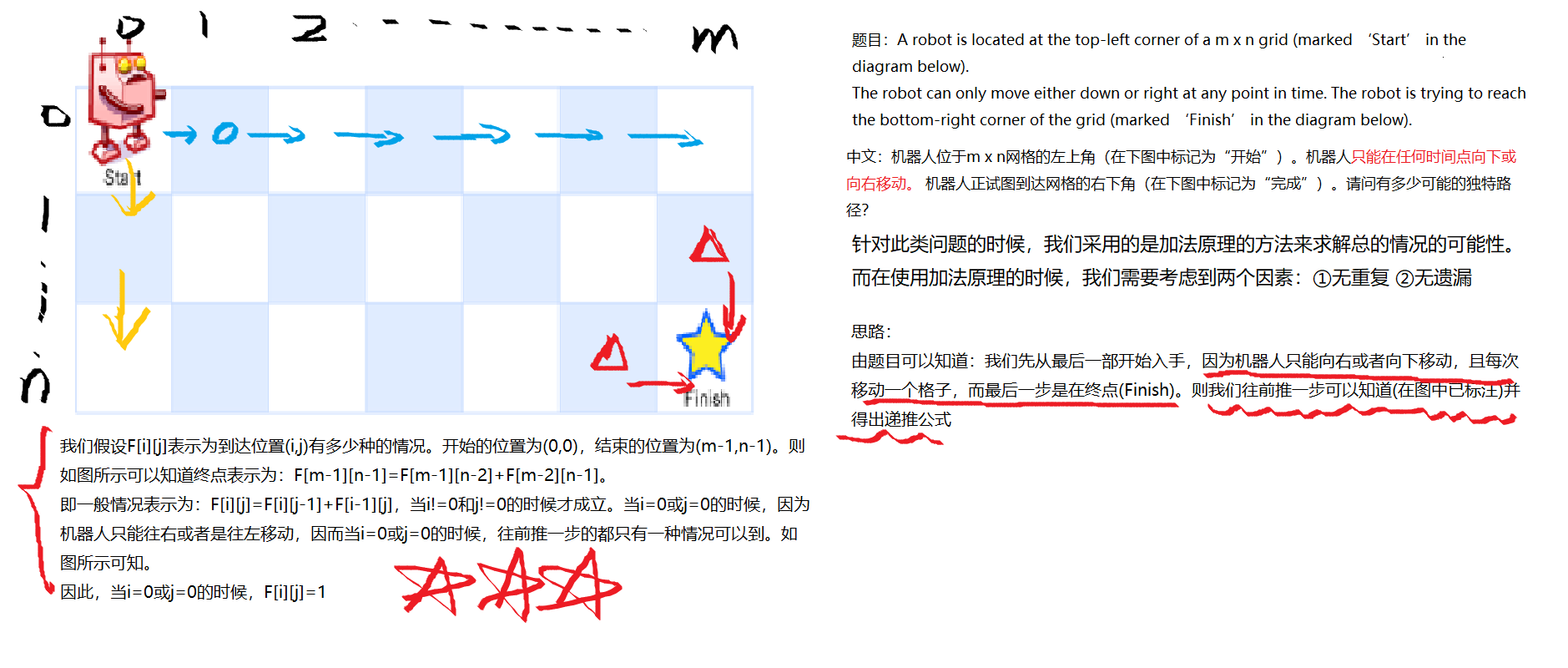
该题目由上述图片可以知道：

 

m,n=map(int,input().split())
F=[[0]*n for i in range(m)] //申请一个二维数组a，a是一个吗m行、n列的一个二维数组
for j in range(0,m):  //表示为我们的计算顺序，我们是从左到右，从上到下进行依次的记录
    for k in range(0,n):
        if j==0 or k==0: //表示当机器人在第一排或者是这一列进行运动时(如图所示)，因为机器人只能向右或向下运动，因而F[j][k]=1,
            F[j][k]=1      其中F[j][k]表示为机器人到(j,k)位置的可能情况种类数
        else:
            F[j][k]=F[j-1][k]+F[j][k-1] //当机器人不在j=0 or k=0上的时候，机器人到任意一个位置上的次数满足F[j][k]=F[j-1][k]+F[j][k-1]这个式子
print(F[j][k])

 例子：Jump Game

You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.

Return true if you can reach the last index, or false otherwise.

中文：给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度，判断你是否能够到达最后一个下标。

思路：由下图所示可以知道

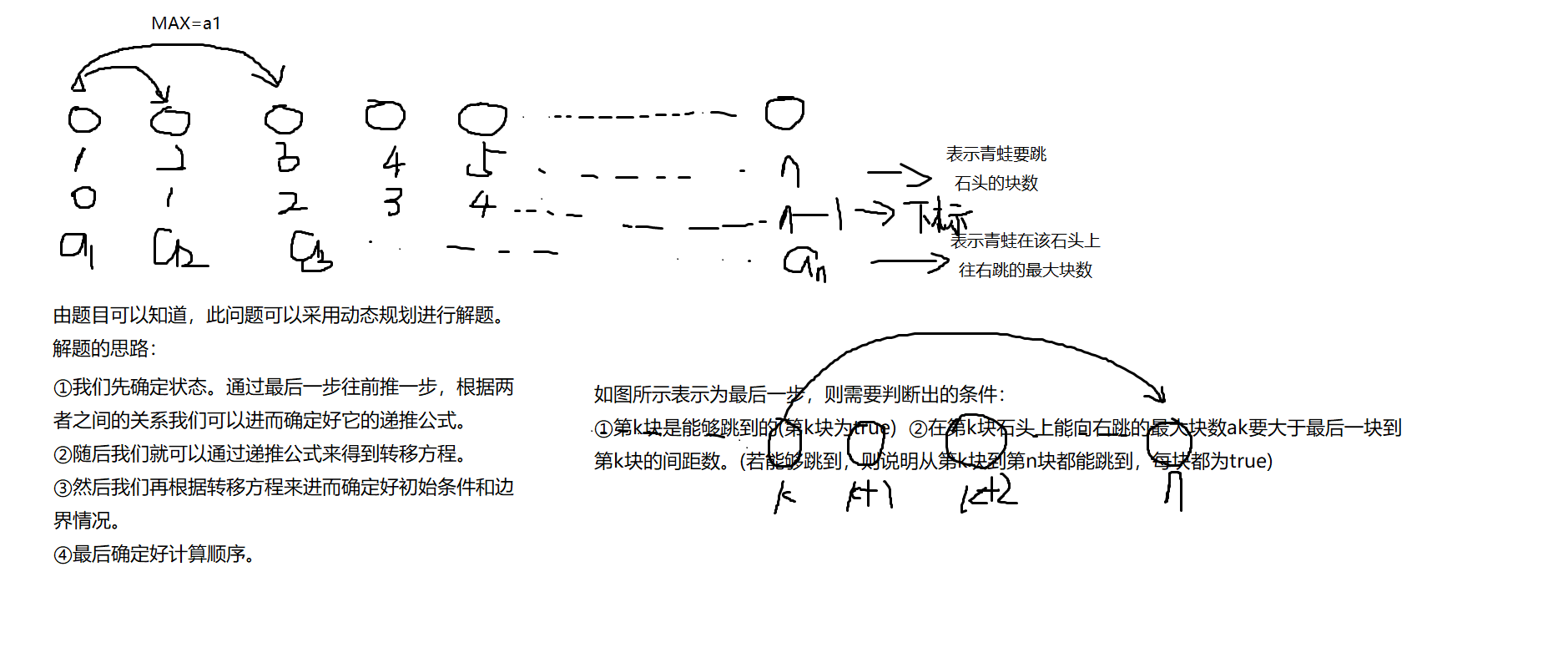
a=[]
for i in input().split(','):
    a.append(eval(i))
b=len(a)
F=[False]*b //创建一个数组，用来记录每一块的情况，用来判断该块石头能不能到达
F[0]=True //表示第一块是能够跳到的，而且青蛙本身是从第一块开始往后跳
for j in range(0,b): //遍历每一块的石头
    if F[j]==True:  //若青蛙可以跳到这块石头上
        c=j+a[j]  //记录下青蛙在该石头上能向右跳多少块石头
        k=j+1
        while k<=c: //将能跳到的石头都标记一下
            if k>b-1: //表示可以跳到最后一块上
                break
            else:
                F[k]=True
                k+=1
print(F[j])

总结：

记得先判断该问题是否符合动态规划的求解方法。若该问题适合用动态规划进行解决，则我们再根据上述的四步操作来进行理解并书写，这样更加容易让我们理解写出程序。(要多多的练习动态规划的题目)