函数的使用
一.教学目的
了解函数重载、值传递和地址传递并且学会编写递归函数
二.教学重点
函数重载、值传递和地址传递、递归函数
三.问题思考
1.为什么要用函数？
2.为什么要用函数重载？
3.什么是值传递？
4.什么是地址传递？
5.如何编写递归函数？
四.解决问题
1.为什么要用函数?
函数编写好以后，可以被重复使用，使用时可以只关心函数的功能和使用方法而不必关心函数功能的具体实现，这样有利于代码的重用，可以提高开发效率、增强程序的可靠性，也便于分工合作和修改维护。(教材64页)
2.为什么要用函数重载？
前提须知：
(a)函数重载是指两个以上的函数，具有相同的函数名，但是形参的个数或者类型不同，编译器根据实参和形参的类型及个数的自动匹配，自动确定调用哪一个函数，这就是函数的重载。(教材84页)
（b)注意：
1.不要将不同功能的函数定义为重载函数
2.重载函数的形参必须不同：个数不同或者类型不同
| int add(int x,int y); float add (float x,float y); |
解决问题：
以上是一个重载函数，我们可以使他们执行一系列的操作，但是这两个分别是应用在不同的参数类型上的。至于选择哪一个函数进行调用，我们不需要去管他，这是编译器要自己判断的。
假如我们有好多种类型，我们要让他们拥有相同的功能，每一种类型我们都给他起一个函数名，当我们要调用它们的时候，我们可能无法记住它们每一个函数名。但是如果我们使用重载函数，我们就不需要考虑这些东西，我们只需要定义重载函数，至于什么时候用哪个函数，就可以交给编译器自己。
应用举例：
利用重载函数，分别求两个整数的平方和两个实数的平方和
#include <iostream>
using namespace std;
int sum(int a,int b)
{
return a*a+b*b;
}
double sum(double a,double b)
{
return a*a+b*b;
}
int main()
{
int m,n;
cout<<"请输入两个整数:";
cin>>m>>n;
cout<<"两个数的平方和结果是:"<<sum(m,n)<<endl;
double x,y;
cout<<"请输入两个实数:";
cin>>x>>y;
cout<<"两个数的平方和结果是:"<<sum(x,y)<<endl;
return 0;
}
运行结果：
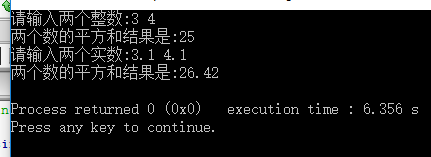
3.什么是值传递？
值传递是指当发生函数调用时，给形参分配内存空间，并用实参来初始化形参（直接将实参的值传递给形参）这一过程是参数值的单向传递过程(教材78页)
单向传递：可以理解为被调用函数中，形参值可以改变，但不影响主函数的实参值。
应用举例:
#include <iostream>
using namespace std;
void swap(int a,int b){
int t=a;
a=b;
b=t;
}
int main()
{
int x=5,y=10;
cout<<"x="<<x<<" y="<<y<<endl;
swap(x,y);
cout<<"x="<<x<<" y="<<y<<endl;
return 0;
}
运行结果：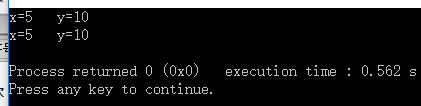 
从上面我们可以看到值传递没有实现交换的目的。
4.什么是地址传递
地址传递时值将实参变量的地址值传递给形参，这里面形参是个指针，让形参的指针指向实参的地址，这样就可以改变实参变量的值了。
应用举例：
#include<iostream>
using namespace std;
int swap(int *a, int *b)
{
int t;
t = *a;
*a = *b;
*b = t;
return 0;
}
int main()
{
int x=5,y=10;
cout<<"x="<<x<<" y="<<y<<endl;
swap(x,y);
cout<<"x="<<x<<" y="<<y<<endl;
return 0;
}
运行结果：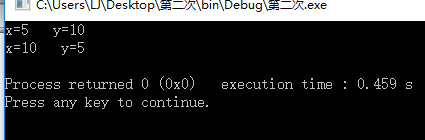
我们可以看到传地址将可以实现函数的交换。
5.如何编写递归函数？
递归函数是可以直接或者间接的调用自身
一个递归函数的调用过程类似于多个函数的嵌套的调用，只不过调用函数和被调用函数是同一个函数。
应用举例：
求n的阶乘
#include<iostream>
using namespace std;
unsigned fac(unsigned n)
{
unsigned f;
if(n==0)
f=1;//递归终止条件
else
f=fac(n-1)*n;//应用递归函数
return f;
}
int main()
{
unsigned n;
cout<<"Enter a postitve interger:";
cin>>n;
unsigned y=fac(n);
cout<<n<<"!="<<y<<endl;
return 0;
}
运行结果：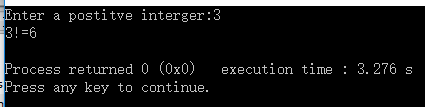 
例题分析（教材77页）
汉诺塔问题
void hanoi(int n,char src,char medium,char dest)//src为原始，medium为中转，dest为目标
{
if(n==1)
move(src,dest);
else{
hanoi(n-1,src,dest,medium);//对应的也分别是原始，中转和目标
move(src,dest);
hanoi(n-1,medium,src,dest);
}
}
可以看出在写递归函数的时候要看递归的出口即边界条件，在此题中不需要具体看碟子一次次怎样移动只需要看碟子从哪里移动到哪里。
