进制转化
进制转换是个老问题了，今天恰巧看见。我详细的去分析下它。留一笔吧
二进制的范围是(0-1)， 不包含2
八进制的范围是(0-7) ，不包含8
十六进制的范围是(0-15) ，不包含16
先讲十进制---->二进制的转换，举例子说明的十进制数字12
这里我把十进制的12转换成二进制，该为多少?
十进制转换二进制方法:十进制通通除以2
拿12来开刀
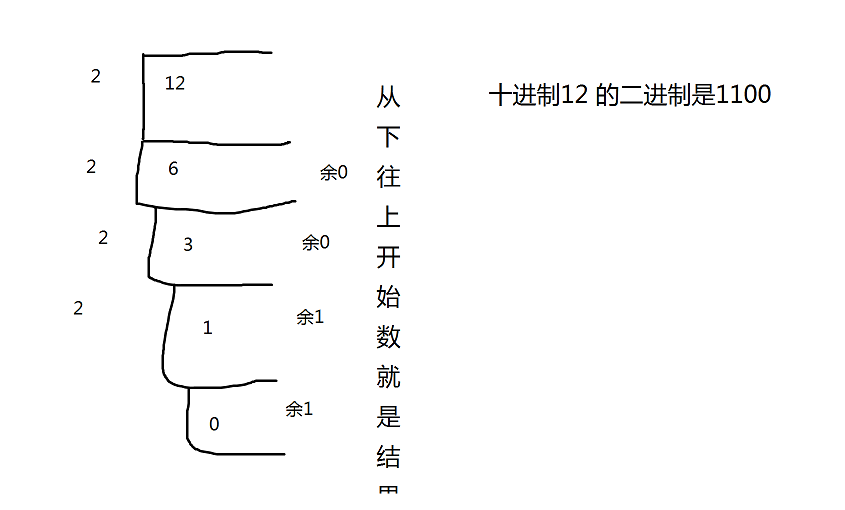
我们每次都除以2直到商为0停止，最后的二进制结果取每次得到的余数
最后得到结果是1100
十进制转换二进制很简单，下面逆向分析，二进制如何转换十进制
随机一个二进制0100，我开始尝试把0100转换成十进制
也很简单
先看一张图
搞清楚上面那张图，下面运算就很简单了
十进制转换成二进制和二进制转成十进制的算法都讲完了。这只是开胃菜。我们继续:
下面是十进制转换成八进制的演示:
学到这里相信大家都已经知道十进制转换成二进制是:十进制数字每次都除以2
那么十进制转换成八进制是否有这种类似的规律可言呢?
猜的没错，的确如此。十进制转换成八进制就是:十进制数字每次都除以8
我们奖十进制54转换成八进制
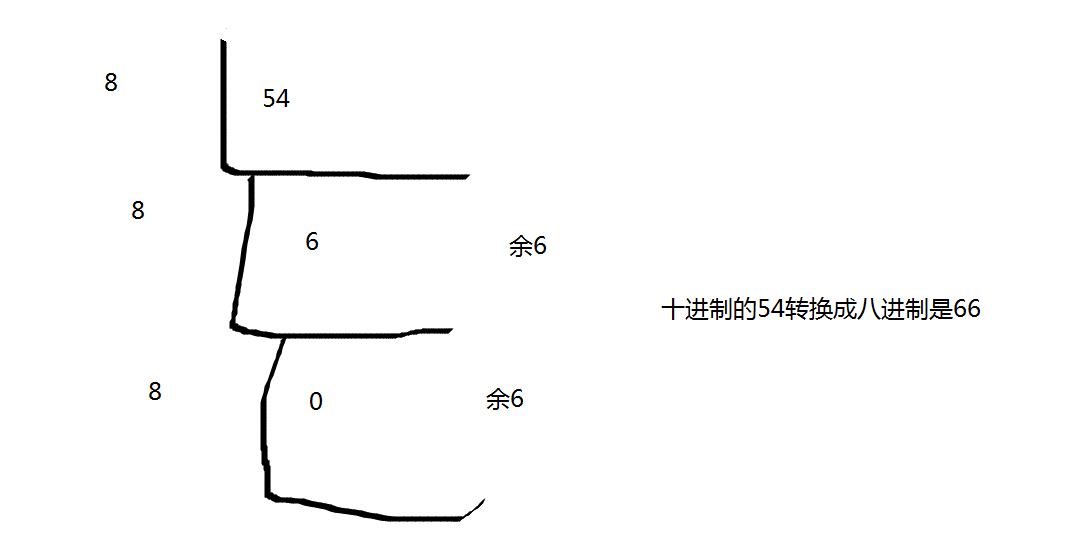
这里我算出来是66
验证下答案:
结果就是余数从下往上数，这个我在前面就讲过。
现在开始演示八进制转换成十进制
在上面的知识学习中我们发现二进制转换成十进制是:二进制数字*2^n次方(n随位置的变化而变化)
那么八进制转换成十进制是否也存在这种规律呢？
答案是必然的
举例子说明的八进制数字是64，把64转换成十进制是多少呢?
这里我算出来是52
验证下结果:
没问题
刚刚我讲解了十进制转换成八进制，同时也讲解了八进制转换十进制的方法
现在我们需要加大难度，我们尝试将二进制转换成八进制
该怎么做？这里存在一个算法公式:二进制每三个位置等于一个八进制数
理解这个公式就很轻松的做这种转换
我们随机输入二进制数字进行测试:0100101010101
就选择我红色标记的二进制数，将它转换成八进制
所以二进制0100101010101的八进制数是4525
演示完二进制转换成八进制，那么八进制转换成二进制呢？
一个道理，只要记住:每三个二进制=一个八进制数
假设八进制数字是15，把15转换成二进制，我来演示下:
验证结果:
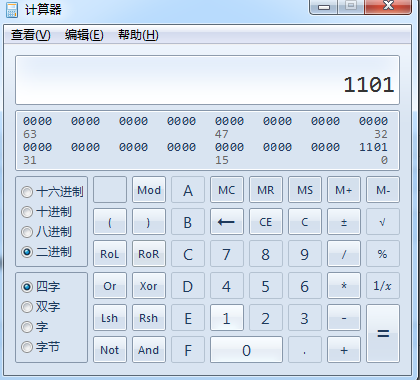
#八进制转换成二进制还可以这样:先八进制转换成十进制然后在十进制转换成二进制，但是那样太麻烦，这样一次性算好比较好。
假如你能从最前面看到这里，那我表示佩服。哈哈
回顾上面讲的，我们已经讲完了:十进制和二进制之间的转换和十进制，八进制，二进制之间的转换
写到这里，笔者自己也有点乱了，不要说了，一鼓作气!下面要介绍是十六进制!
首先讲解十进制转换成十六进制
在进行转换之前学了解一个十六进制的基础知识:
从16进制开始，不是简单的都是数字了开始多了字母!
好了咱们继续，这里我选取的十进制数字是:15
我开始将十进制15转换成十六进制，会是多少呢?
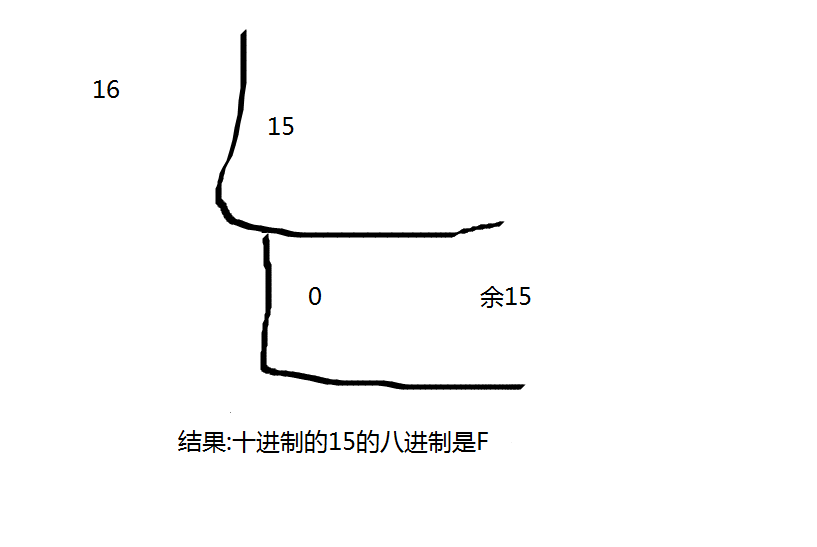
现在我们尝试把十六进制转换成十进制该怎么转换?
和之前二进制转换十进制和八进制转换成十进制一个道理，这里是:十六进制数字*16^n次方(n随位置的变化而变化)
这里演示的十六进制数字是:23
这里我将十六进制的23转换成十进制:
演示完了十进制和十六进制之间的转换，现在开始演示十六进制转换成八进制
选取16进制23
转换思路有点多。。。我随机选取一种吧，将23先转换成十进制，上面我已经做过了是35
将十进制35转换成八进制就是:
这个其实不难，就是两次转换而已
现在演示最关键的就是二进制和十六进制之间的转换
在讲解之前先讲解一个很重要的公式:每四个二进制=一个八进制数 (正所谓2^4=16)
那么随机选择一个二进制数字:0100100011
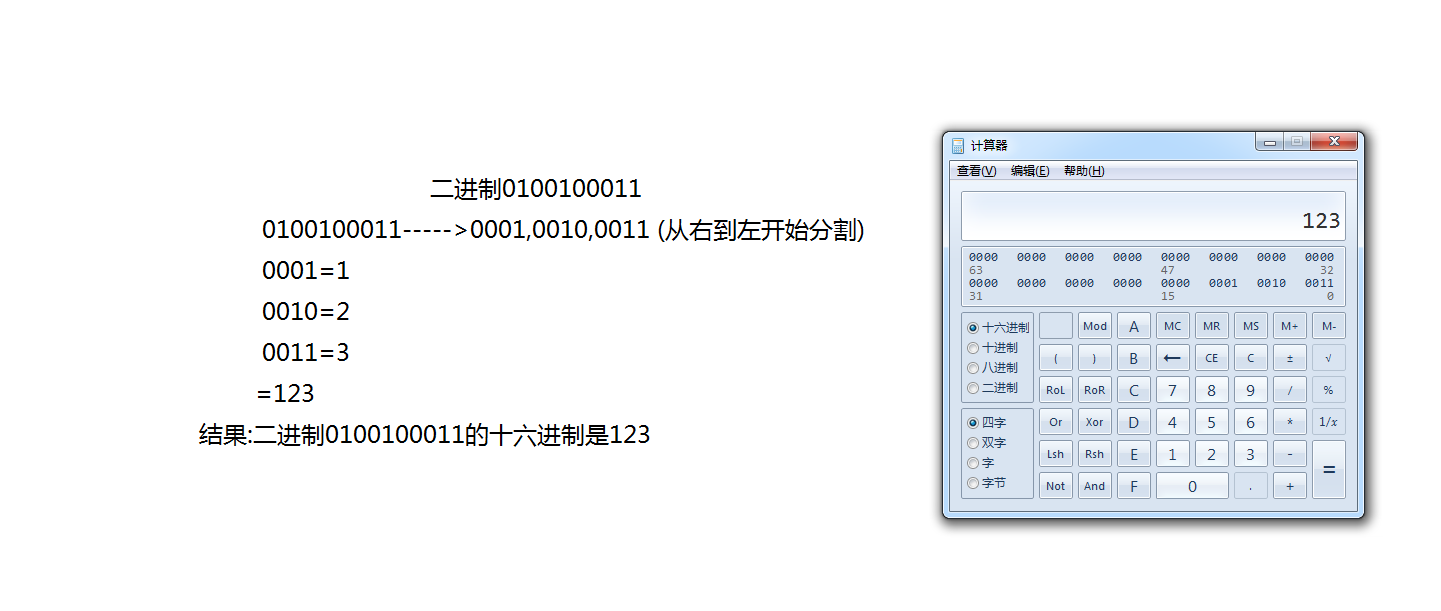
二进制转换成十六进制讲完，下面是十六进制转换成二进制
随机选取十六进制:15
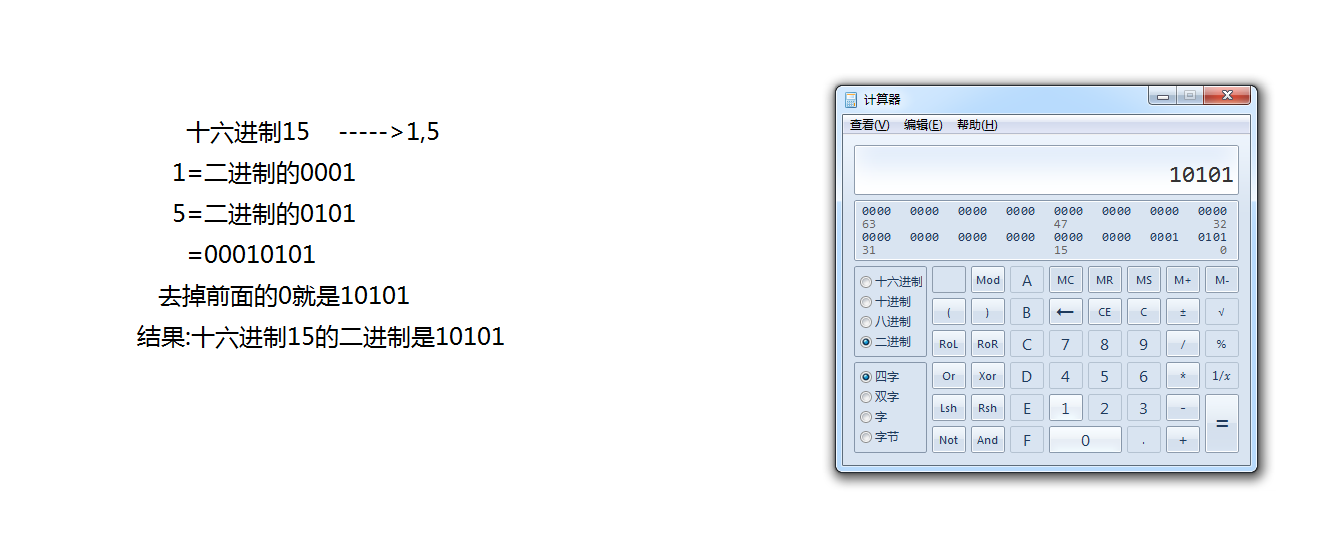
感觉该讲的我都讲完了，写完了整个过程，首先我自己收获颇多，记录下这一笔!
-----------不忘初心，方得始终!
转自https://www.cnblogs.com/piaomiaohongchen/p/8053245.html
