【Elite量化策略实验室】大类资产ETF轮动策略 - 2

发布于VeighNa社区公众号【vnpy-community】

原文作者：丛子龙 | 发布时间：2023-8-31

增加同时持仓数量

在探讨多标的资产投资策略的过程中，或许有些同学会产生疑问：为何不同时持有多个合约？这样不仅可以分散风险，还能够捕捉更多有利的行情机会。所以接下来我们就在上篇文章策略的基础上，引入多个投资标的同时持仓的逻辑。

在新的策略中，我们仍然依据R方和斜率的乘积来评估趋势的强弱，得出趋势强弱评分（score）。然而，这次与之前的策略不同，我们决定从中选出两个得分较高的ETF来进行买入持有，而不再仅限于选择一个。每次买入开仓时，将每个选中的ETF买入数量设定为固定资本（fixed_capital）的一半。

来看一下调整后的历史回测绩效表现：

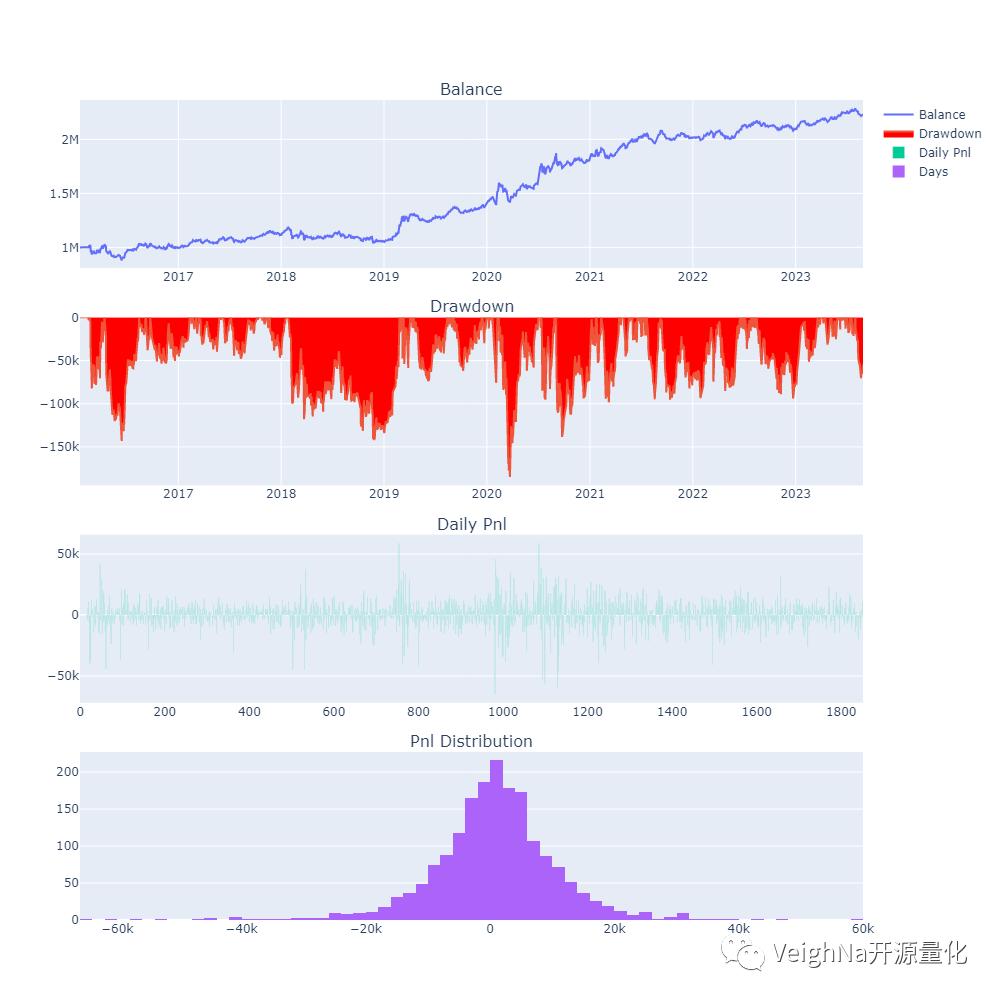
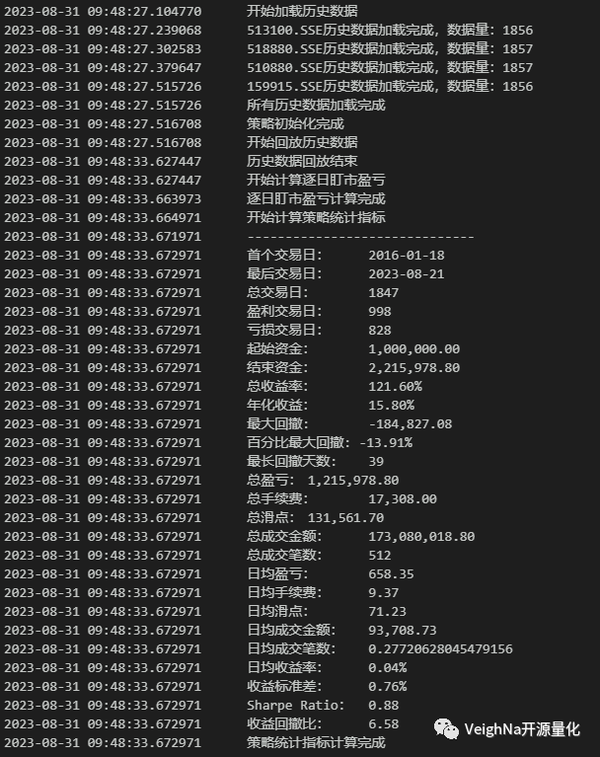
调整的结果展示在历史回测的绩效数据中：尽管年化收益略微下降，但百分比回撤和收益回撤比得到了改善，夏普比率相较于原策略也有所提升。

以上改进反映在实际交易中将会转化为更良好的持仓体验，为投资者带来更加稳定和满意的交易结果，具体绩效统计数值对比请看下表：

统计数值	原策略	新策略
总收益率	139.54%	121.60%
年化收益	18.04%	15.80%
百分比回撤	-18.74%	-13.91%
夏普比率	0.81	0.88
收益回撤比	4.62	6.58

策略代码实现

新的策略代码中引入了名为【holding_size】的变量，用来控制同时持仓的合约数量。

对于记录当前持仓合约的策略成员变量，需要由之前的单一字符串【holding_symbol】，改为字符串列表【holding_symbols】。由于列表属于Python中的可变对象，因此【holding_symbols】的创建需要移动到策略的【on_init】初始化函数之下。

经过调整后的策略模板创建部分的代码如下：

class EtfRotationStrategy(StrategyTemplate):
    """ETF轮动策略"""

    author: str = "CZL"

    regression_window: int = 25         # 线性回归窗口
    holding_size: int = 2               # 同时持仓数量
    fixed_capital: int = 1_000_000      # 固定持仓市值

    parameters = [
        "regression_window",
        "holding_size",
    ]

    def on_init(self) -> None:
        """策略初始化"""
        # 确保缓存数据足够回归计算
        size: int = self.regression_window + 1
        
        # 创建缓存持仓合约的列表
        self.holding_symbols: list = []

        # 创建每个合约的时序数据容器
        self.ams: dict[str, ArrayManager] = {}

        for vt_symbol in self.vt_symbols:
            self.ams[vt_symbol] = ArrayManager(size)

        self.write_log("策略初始化")

在on_bars回调函数下需要做出相应的更改，这里我们也将目标交易执行的逻辑进行了优化，避免在持仓ETF没有发生变化时进行不必要的调仓：

    def on_bars(self, bars: dict[str, BarData]) -> None:
        """K线切片推送"""
        # 更新K线到时序容器
        score_data: Dict[str, float] = {}

        for vt_symbol, bar in bars.items():
            am: ArrayManager = self.ams[vt_symbol]
            am.update_bar(bar)
            
        for vt_symbol, bar in bars.items():
            am: ArrayManager = self.ams[vt_symbol]
            if not am.inited:
                return
            
            # 对ETF进行打分
            score_data[vt_symbol] = calculate_score(am.close[-self.regression_window:])
            
            # 重置目标仓位
            self.set_target(vt_symbol, 0)
            
        # 对score进行排序，切片选出得分靠前的N个ETF
        top_ranked = sorted(score_data, key=score_data.get, reverse=True)[:self.holding_size]
        
        # 如果新一轮入选的ETF与目前持仓不一样，进行调仓
        if set(top_ranked) != set(self.holding_symbols):
            self.holding_symbols = top_ranked
            for security in self.holding_symbols:
                price: float = bars[security].close_price
                
                # 每个入选的合约获得同样资金
                volume: int = 100 * int((self.fixed_capital / self.holding_size) / (price * 100))
                self.set_target(security, volume)
            
            # 根据设置好的目标仓位进行交易
            self.rebalance_portfolio(bars)
        
        # 推送UI更新
        self.put_event()

策略历史回测

改进后策略的历史回测依旧使用上篇文章中用到的数据，具体的回测参数配置如下：

字段名	字段值
本地代码	513100.SSE
518880.SSE
510880.SSE
159915.SZSE
K线周期	日线
开始日期	2016-01-01
结束日期	2023-08-21
手续费率	0.0001
交易滑点	0.001
合约乘数	1
价格调动	0.001
回测资金	100W

策略参数优化

目前策略已经拥有了两个核心参数【regression_window】和【holding_size】，那么到底这两个参数的数值要怎么设置才能实现更好的策略绩效，接下来的任务自然就是参数优化。

考虑到回测中使用的是日线数据（计算速度较快），所以直接选择暴力穷举优化，下面使用热力图的方式来直观展示参数优化的结果：

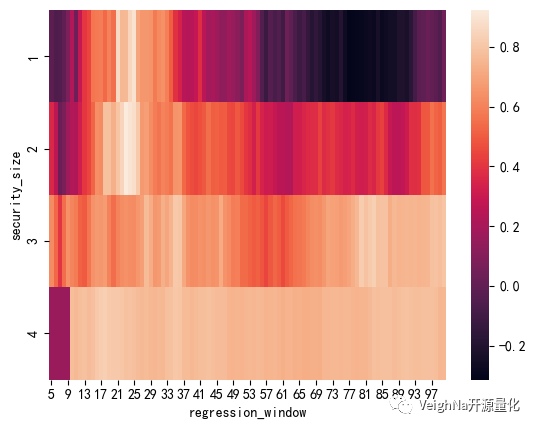
上图中颜色越浅，代表夏普比率（优化的目标函数）越高。可以看出，排名靠前的参数组合聚集在【holding_size】为2，【regression_window】为25~29的区域。

以下是运行参数优化和绘制热力图的代码，可以根据自己的实际需求进行调整：

# 这里需要用到pandas和seaborn两个包
import pandas as pd
import seaborn as sns

# 先运行穷举优化，并将优化结果缓存
setting = OptimizationSetting()
setting.set_target("sharpe_ratio")
setting.add_parameter("holding_size", 1, 4, 1)
setting.add_parameter("regression_window", 5, 100, 1)
result = engine.run_optimization(setting)

# 创造一个空字典用于缓存
data = {}

# 遍历解析result中数据，并缓存进入data
for i in range(len(result)):
    d.setdefault('holding_size', []).append(eval(result[i-1][0])['holding_size'])
    d.setdefault('regression_window', []).append(eval(result[i-1][0])['regression_window'])
    d.setdefault('sharpe_ratio', []).append(result[i-1][1])
    
# 将数据转化为DataFrame，并按照夏普比率的大小进行排序
sorted_result = (pd.DataFrame(data)
                  .sort_values('sharpe_ratio', ascending=False)
                  .reset_index(drop=True))

# 将数据格式转化为pivot table方便绘制热力图
pivoted_table = sorted_result.pivot("holding_size", "regression_window", "sharpe_ratio")

# 绘制热力图
sns.heatmap(pivoted_table)

对于双参数的优化场景，使用热力图可以清晰地观察不同参数组合下策略的绩效表现。这样的分析能够帮助更好地把握参数对策略影响的程度，为进一步的策略改良决策提供有力的依据。

下篇文章中我们准备扩展策略交易的大类资产ETF范围，看看能否获得更加稳健的回测结果。

完整策略代码和回测数据文件，可以通过【VeighNa进阶用户交流群】获取：

免责声明

文章中的信息或观点仅供参考，作者不对其准确性或完整性做出任何保证。读者应以其独立判断做出投资决策，作者不对因使用本报告的内容而引致的损失承担任何责任。