sinα±cosα与sinα·cosα之间的恒等式

No.1

恒等式

（1）（sinα+cosα)²=1+2sinα·cosα

（2）（sinα-cosα)²=1-2sinα·cosα

（3）（sinα+cosα)²+（sinα-cosα)²=2

由上述恒等式可知：若给出sinα+cosα，sinα-cosα，sinα·cosα中任意一个式子的值，则可求出另外两个的值.

No.2

sinα±cosα的符号的判断方法

（1）sinα-cosα的符号判断方法

由三角函数的定义知，

1>当α的终边在直线 y=x 上时，sinα=cosα即sinα-cosα=0；

2>当α的终边在直线y=x的 上 半部分区域内时（如下图圆中深色部分），sinα>cosα，即sinα-cosα > 0；

3>当的终边在直线y=x的 下 半部分区域内时，sinα < cosα，即sinα-cosα < 0.

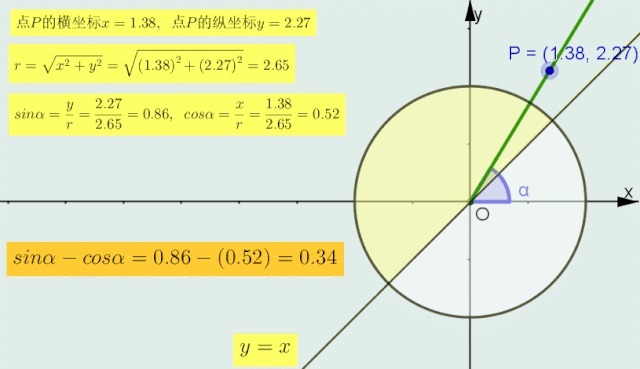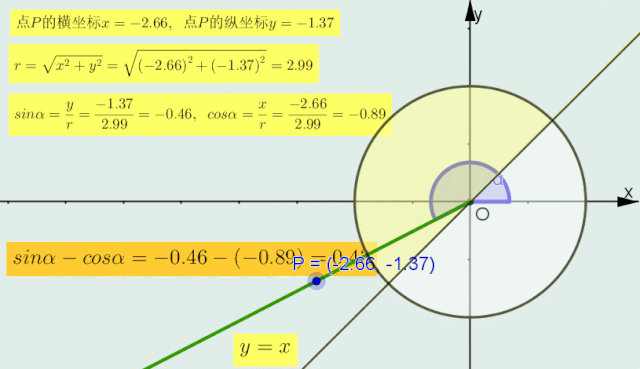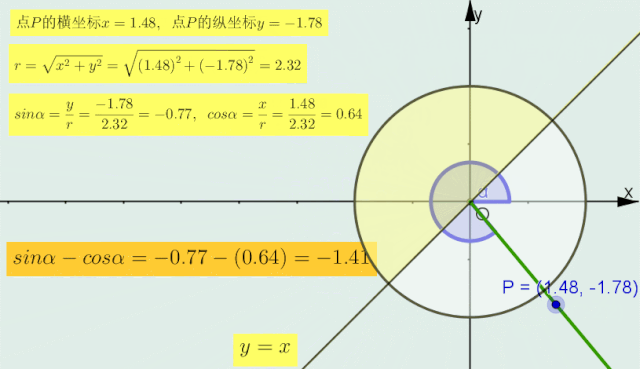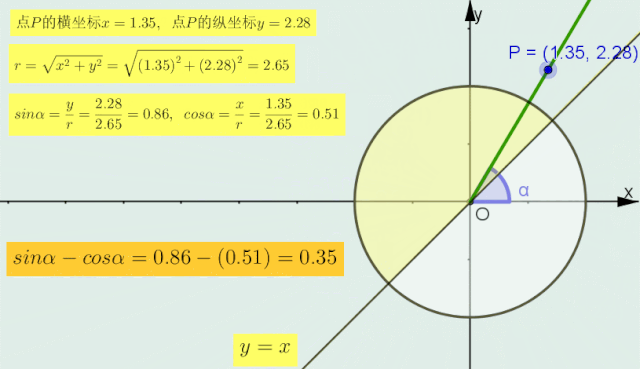
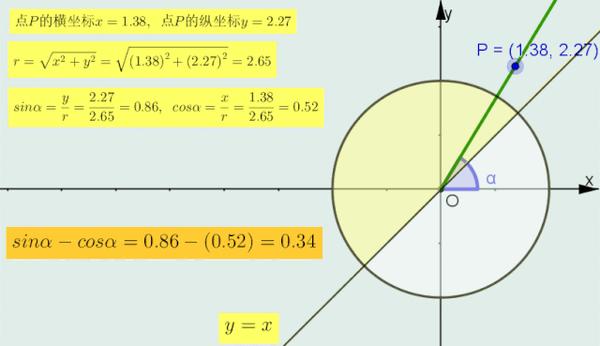
正弦减余弦符号

（2）sinα+cosα的符号判断方法

由三角函数的定义知，

当α的终边在直线 y=-x 上时，sinα=-cosα即sinα+cosα=0；

当α的终边在直线y=x的 上 半部分区域内时（如下图圆中深色部分），sinα > -cosα，即sinα+cosα > 0；

当α的终边在直线y=x的 下 半部分区域内时，sinα < -cosα，即sinα+cosα < 0.

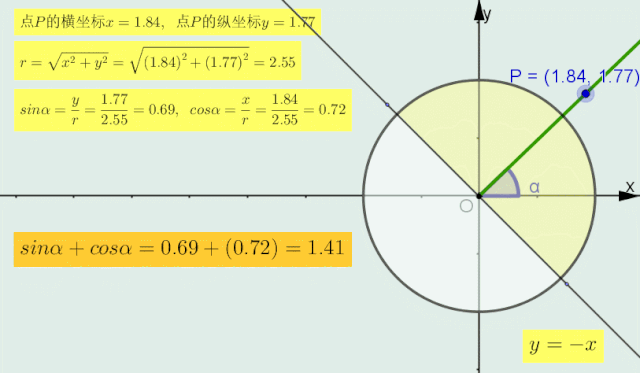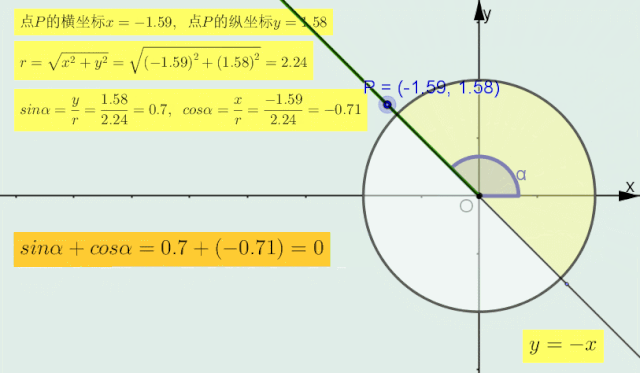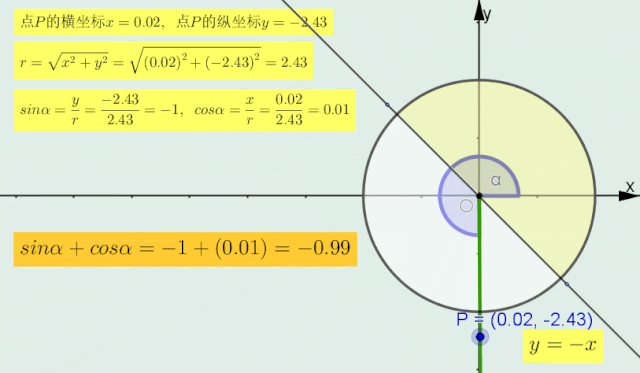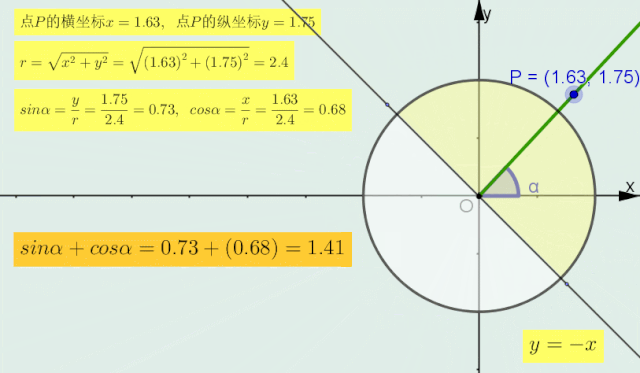
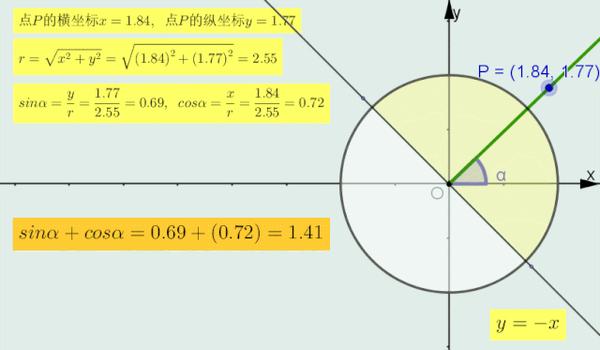
正弦加余弦符号

（3）总结

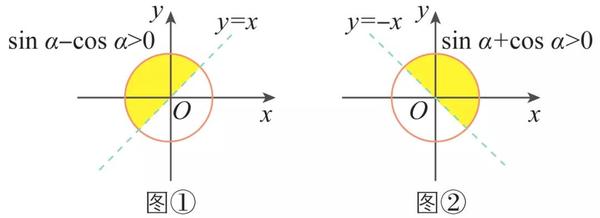
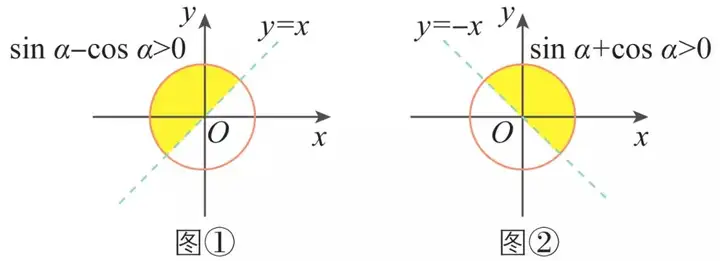
示范例题

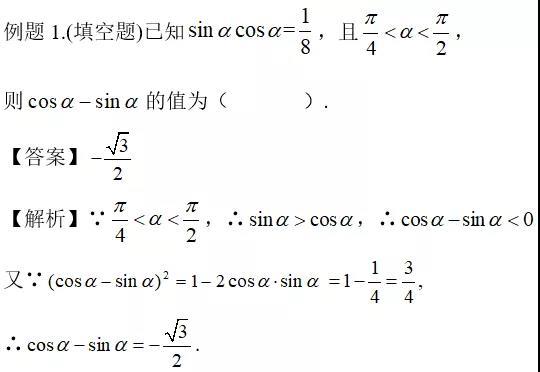
点拨:

sinα+cosα，sinα-cosα，sinα·cosα三式中，可以“知一求二”（平方关系作为桥梁）.

例题2.(填空题)已知θ是第二象限角，sinθ,cosθ是关于x的方程3x²-x+t=0(t∈R）的两根，则cosθ-sinθ=（ ）.

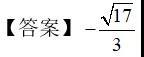
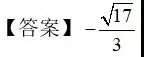
【解析】∵sinθ,cosθ是关于x的方程3x²-x+t=0(t∈R）的两根

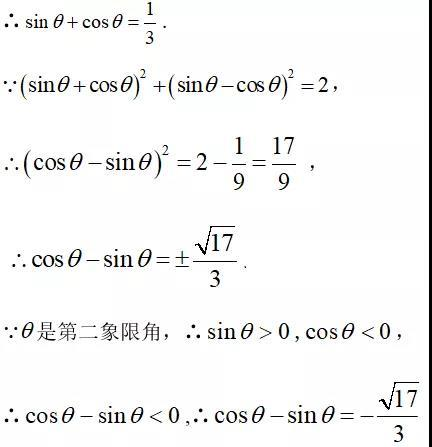
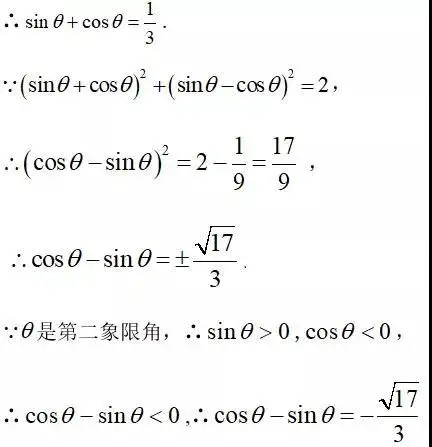
内容摘自：包学习APP_动态教辅《同角三角函数的基本关系式（数学新教材人教B必修三7.2.3）》，欢迎下载学习更多知识
转自：https://zhuanlan.zhihu.com/p/98155994