PriorityQueue及二叉堆

PriorityQueue是一个优先级队列，底层是小顶堆实现

概念

• 优先级队列

通常的队列是先进先出，那有一种特殊的队列并不是先进先出，而是根据优先级的顺序出队

• 二叉堆

二叉堆是一种数据结构，堆是一种特殊的二叉树，满足一下条件的二叉树

1.该二叉树必须是一个完全二叉树。

2.子节点的值总是单调的。这里又分为两种情况，如果子节点总是小于等于父节点，那么整体的树顶元素就越大，那么我们叫它大顶堆，反过来子节点总是大于等于父节点，那么我们叫它小顶堆

• 完全二叉树

元素是按照从上到下层级，从左到右的顺序排列的树形结构

• 堆

上面我们说了二叉堆，那么其实堆也可以是多叉堆，多叉堆同理也有上面两个类似性质。1.完全多叉树 2.父子节点单调性

二叉堆

虽说这里的数据结构是二叉树，但实际装数据的容器，或者说底层还是使用的数组,PriorityQueue中源码:

transient Object[] queue; // non-private to simplify nested class access

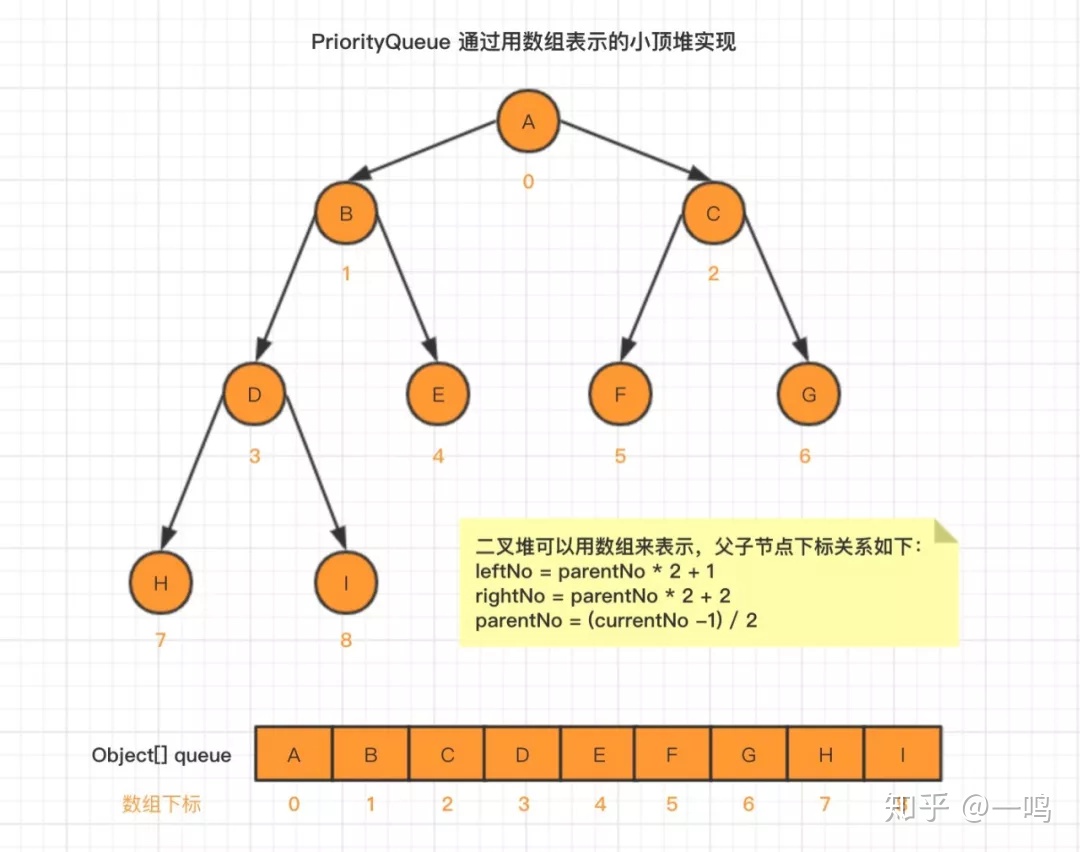
在上图中，我们给每个元素的下标做了标注，足够细心的你会发现，数组下标，存在以下关系：

leftNo = parentNo * 2 + 1
rightNo = parentNo * 2 + 2
parentNo = (currentNo -1) / 2

这样一来，我们在得到任意节点的情况下，就能通过该公式找到它的父节点和子节点

入堆

当有了基础的概念和理论之后，我们来构建堆，像堆中加入元素就是构建堆的一个过程。

 /**
     * Inserts the specified element into this priority queue.
     *
     * @return {@code true} (as specified by {@link Collection#add})
     * @throws ClassCastException if the specified element cannot be
     *         compared with elements currently in this priority queue
     *         according to the priority queue's ordering
     * @throws NullPointerException if the specified element is null
     */
public boolean add(E e) {
    return offer(e);
}
    

 /**
     * Inserts the specified element into this priority queue.
     *
     * @return {@code true} (as specified by {@link Queue#offer})
     * @throws ClassCastException if the specified element cannot be
     *         compared with elements currently in this priority queue
     *         according to the priority queue's ordering
     * @throws NullPointerException if the specified element is null
     */
public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length) //如果queue数组中的数据满了，扩容
        grow(i + 1);
    siftUp(i, e);   //siftUp，上浮元素
    size = i + 1;
    return true;
}

 private void siftUp(int k, E x) {
        if (comparator != null)//比较器优先
            siftUpUsingComparator(k, x, queue, comparator);
        else
            siftUpComparable(k, x, queue);
    }

 /**
     * Increases the capacity of the array.
     *
     * @param minCapacity the desired minimum capacity
     */
    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = ArraysSupport.newLength(oldCapacity,
                minCapacity - oldCapacity, /* minimum growth */
                oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
                                           /* preferred growth */);
        queue = Arrays.copyOf(queue, newCapacity);
    }
    
    
    

offer方法中我们可以看到的流程

• 如果queue数组中的数据满了，扩容
• siftUp，上浮元素
  • 因为元素的父子元素具有单调性，所以可以通过比较，和父节点交换位置，直到找到它合适的位置
    • 这里我们看到的是 比较器（siftUpUsingComparator）优先。
  • 合适的位置指的是 满足 单调性 的位置

出堆

/**
     * Retrieves and removes the head of this queue,
     * or returns {@code null} if this queue is empty.
     *
     * @return the head of this queue, or {@code null} if this queue is empty
     */
 public E poll() {
        final Object[] es;
        final E result;

        if ((result = (E) ((es = queue)[0])) != null) {//取出第一个元素（索引为0）
            modCount++;
            final int n;
            final E x = (E) es[(n = --size)];//获得最后一个元素
            es[n] = null;//最后一个元素置空
            if (n > 0) {
                final Comparator<? super E> cmp;
                if ((cmp = comparator) == null) //比较器优先
                    siftDownComparable(0, x, es, n);//然后做下层操作
                else
                    siftDownUsingComparator(0, x, es, n, cmp);//然后做下层操作
            }
        }
        return result;
    }
    
    private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
        // assert n > 0;
        Comparable<? super T> key = (Comparable<? super T>)x;
        int half = n >>> 1;           // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = es[child];
            int right = child + 1;
            if (right < n &&
                ((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
                c = es[child = right];
            if (key.compareTo((T) c) <= 0)
                break;
            es[k] = c;
            k = child;
        }
        es[k] = key;
    }
    
      private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
        // assert n > 0;
        Comparable<? super T> key = (Comparable<? super T>)x;
        int half = n >>> 1;           // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least 翻译  假设左孩子是更小的
            Object c = es[child];
            int right = child + 1;
            if (right < n &&
                ((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
                c = es[child = right];  //得到较小的孩子
            if (key.compareTo((T) c) <= 0)  //用教小的孩子做比较，做交换
                break;
            es[k] = c;
            k = child;
        }
        es[k] = key;
    }

poll过程如下

• 首先取出索引为0的元素，堆顶元素
• 把索引最大的元素拿到堆顶做下沉操作
  • 如果PriorityQueue构造的时候拥有比较器就用比较器来做下沉比较，否者使用元素继承的Comparable比较性做比较

Queue常见对外方法

• boolean add(e) 添加
• boolean offer(E e) 同add相同
• E poll() 取出堆顶元素，也就是数组索引为0的元素，size会减少。size=0时会得到 null
• E peek() 读取堆顶元素，size不会减少。size=0时会得到 null
• E remove() 和poll()功能相同，只是会@throws NoSuchElementException if this queue is empty
• E element() 和peek()功能相同，只是会@throws NoSuchElementException if this queue is empty