RSA详解(Java实现)
RSA密码
RSA密码是1978年美国麻省理工学院三位密码学者R.L.Rivest、A.Shamir和L.Adleman提出的一种基于大合数因子分解困难性的公开密钥密码。由于RSA密码既可用于加密,又可用于数字签名,通俗易懂,因此RSA密码已成为目前应用最广泛的公开密钥密码。
RSA加解密算法
1.随机地选择两个大素数p和q,而且保密;
2.计算n=pq,将n公开;
3.计算φ(n)=(p-1)(q-1),对φ(n)保密;
4.随机地选取一个正整数e,1<e<φ(n)且(e,φ(n))=1,将e公开;
5.根据ed=1(mod φ(n)),求出d,并对d保密;
6.加密运算:C=Me(mod n);
7.解密运算:M=Cd(mod n)。
注意:在加密运算和解密运算中,M和C的值都必须小于n,也就是说,如果明文(或密文)太大,必须进行分组加密(或解密)。
RSA算法细节
实现RSA算法,主要需要实现以下几个部分:
1.对大数的素数判定;
2.模逆运算;
3.模指运算。
对大数的素数判定
一个较小的数是否为素数,可以用试除法来判定,而如果这个数很大的话,试除法的效率就会变得很低下。也就是说,试除法不适用于对大数进行素数判定,所以对大数的素数判定一般采用素数的概率性检验算法,其中又以Miller算法最为常见。
使用素数的概率性检验算法判定一个数是否为素数,虽然相比试除法而言效率非常之高,但是对该数的判定结果并不准确。该算法通过循环使用Miller算法来提高判定结果的正确性。
素数的概率性检验算法的流程:对于奇整数n,在2~n-2之间随机地选取k个互不相同的整数,循环使用Miller算法来检验n是否为素数。若结果为true,则认为n可能为素数,否则肯定n为合数。
一轮Miller算法判定大整数n不是素数的概率≤4-1,所以,素数的概率性检验算法判定大整数n不是素数的概率≤4-k(k为Miller算法的循环次数)。
Miller算法
若n为奇素数,则对∀a∈[2,n-2],由于a与n互素,根据欧拉定理可得aφ(n)=an-1=1(mod n)。
若n是奇素数,则不存在1(mod n)的非平凡平方根,即对于x2=1(mod n)的解有且仅有±1。
若n是奇素数,则n-1是偶数。不妨令n=2tm+1(t≥1),则m为n-1的最大奇因子。根据上述两点,不难得出,对∀a∈[2,n-2],∃τ∈[1,t]使得
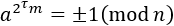
Miller算法正是通过上述的逆否命题而设计出来的,其原理是:对∀a∈[2,n-2],n是一个合数的充要条件是对∀τ∈[1,t]使得

Miller算法的设计思路:令b=am(mod n),如果b=±1(mod n)则n可能是一个素数;否则,b=b2(mod n),并判断是否满足b=-1(mod n)(满足则n可能是一个素数),由此循环t-1次。如果都满足b≠-1(mod n),则n一定是一个合数。
e.m.判定221是否为素数
n=221=22*55+1
所以m=55,t=2
取a=174,则
17455(mod 221)=47
174110(mod 221)=220
所以n要么是一个素数,要么a=174是一个“强伪证”。
再取a=137,则
13755(mod 221)=188
137110(mod 221)=205
所以n是一个合数。
模逆运算
模逆运算就是求满足方程ax=1(mod m)的解x,而ab=1(mod m)有解的前提条件是(a,m)=1,即a和m互素。
对方程ax=1(mod m)的求解可以转换为求解ax+my=1=(a,m),即转换为扩展欧几里德算法。
e.m.求243-1(mod 325)
325=1*325+0*243
243=0*325+1*243
82=325-243=1*325+(-1)*243
79=243-2*82=(-2)*325+3*243
3=82-79=3*325+(-4)*243
1=79-26*3=(-80)*325+107*243
所以
243-1(mod 325)=107
模指运算
模指运算就是对an(mod m)的计算。当指数n的值较大时,如果先求出bn再去模m的话,效率会很低下。所以,对于指数n较大的情况一般采用反复平方乘算法。
反复平方乘算法
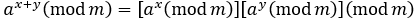
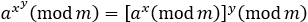
所以,反复平方乘算法的原理是将指数n转化为2的幂之和的形式,即n=2kek+2k-1ek-1+...+2e1+e0,然后根据l1=a2(mod m),l2=a4(mod m)=l12(mod m),...,

最后根据an(mod m)=e0a·e1l1·...·eklk(mod m)求解。
e.m.求2335(mod 101)
35=32+2+1
231(mod 101)=23
232(mod 101)=24
234(mod 101)=242(mod 101)=71
238(mod 101)=712(mod 101)=92
2316(mod 101)=922(mod 101)=81
2332(mod 101)=812(mod 101)=97
所以
2335(mod 101)=97×24×23(mod 101)=14
RSA密码的安全性
密码分析者攻击RSA密码的一种可能途径是截获密文C,通过M=Cd(mod n)求出M。其中,n是公开的,而d是保密的。因为e是公开的,所以可以通过ed=1(mod φ(n))求出d,而φ(n)是保密的。虽然n是公开的,但是φ(n)=(p-1)(q-1)=pq-p-q+1=n-p-q+1,其中p和q是保密的,也就是说欲求得φ(n)必须知道p和q,即必须将n进行因式分解。
小合数的因子分解是容易的,然而大合数的因子分解却是十分困难的。由此可以得出,破译RSA密码的困难性约为对n进行因子分解的困难性。
RSA密码的安全性除了与因子分解密切相关之外,还与其参数p、q、e、d的选取有密切关系。只要合理地选取参数,并正确使用,RSA密码就是安全的。这就是目前RSA密码仍然广泛使用的重要原因。
Java实现
RSA
1 p = BigInteger.probablePrime(new Random().nextInt(100) + 100, new Random()); 2 q = BigInteger.probablePrime(new Random().nextInt(100) + 100, new Random()); 3 n = p.multiply(q); 4 phi_n = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE)); 5 do { 6 e = new BigInteger(new Random().nextInt(phi_n.bitLength() - 1) + 1, new Random()); 7 } while (e.compareTo(phi_n) != -1 || e.gcd(phi_n).intValue() != 1); 8 d = e.modPow(new BigInteger("-1"), phi_n);
1 /** 2 * 加密 3 * <p> C=M^e(mod n) 4 * @param M 5 * @param n 6 * @param e 7 * @return 8 */ 9 public static BigInteger encrypt(BigInteger M, BigInteger n, BigInteger e) { 10 return M.modPow(e, n); 11 }
1 /** 2 * 解密 3 * <p> M=C^d(mod n) 4 * @param C 5 * @param n 6 * @param d 7 * @return 8 */ 9 public static BigInteger decrypt(BigInteger C, BigInteger n, BigInteger d) { 10 return C.modPow(d, n); 11 }
对大数的素数判定
1 /** 2 * 素数的概率性检验算法 3 * @param k 4 * @param n 5 * @return 6 */ 7 static boolean isPrime(int k, long n) { 8 List<Long> a = new ArrayList<Long>(); 9 int t = n - 2 > Integer.MAX_VALUE ? Integer.MAX_VALUE : (int) (n - 2); 10 do { 11 long l = (long) (new Random().nextInt(t - 2) + 2); 12 if (-1 == a.indexOf(l)) 13 a.add(l); 14 } while (a.size() < k); 15 for (int i = 0; i < k; i++) 16 if (! Miller(n, a.get(i))) 17 return false; 18 return true; 19 } 20 static boolean Miller(long n, long a) { 21 long m = n - 1; 22 int t = 0; 23 while (m % 2 == 0) { 24 m /= 2; 25 t++; 26 } 27 long b = modExp(a, m, n); 28 if (b == 1 || b == n - 1) 29 return true; 30 for (int j = 1; j < t; j++) { 31 b = b * b % n; 32 if (b == n - 1) 33 return true; 34 } 35 return false; 36 }
模逆运算
1 /** 2 * 模逆运算 3 * @param b 4 * @param m 5 * @return b^-1(mod m) 6 */ 7 static long modInv(long b, long m) { 8 if (b >= m) b %= m; 9 return exGcd(b, m)[1] < 0 ? exGcd(b, m)[1] + m : exGcd(b, m)[1]; 10 } 11 /** 12 * 扩展欧几里德算法 13 * <p>(a,b)=ax+by 14 * @param a 15 * @param b 16 * @return 返回一个long数组result,result[0]=x,result[1]=y,result[2]=(a,b) 17 */ 18 static long[] exGcd(long a, long b) { 19 if (a < b) { 20 long temp = a; 21 a = b; 22 b = temp; 23 } 24 long[] result = new long[3]; 25 if (b == 0) { 26 result[0] = 1; 27 result[1] = 0; 28 result[2] = a; 29 return result; 30 } 31 long[] temp = exGcd(b, a % b); 32 result[0] = temp[1]; 33 result[1] = temp[0] - a / b * temp[1]; 34 result[2] = temp[2]; 35 return result; 36 }
模指运算
1 /** 2 * 模指运算 3 * @param b 4 * @param n 5 * @param m 6 * @return b^n(mod m) 7 */ 8 static long modExp(long b, long n, long m) { 9 long result = 1; 10 b = b % m; 11 do { 12 if ((n & 1) == 1) 13 result=result*b%m; 14 b = b * b % m; 15 n = n >> 1; 16 } while (n != 0); 17 return result; 18 }
测试
测试数据
p=e86c7f16fd24818ffc502409d33a83c2a2a07fdfe971eb52de97a3de092980279ea29e32f378f5e6b7ab1049bb9e8c5eae84dbf2847eb94ff14c1e84cf568415
q=d7d9d94071fcc67ede82084bbedeae1aaf765917b6877f3193bbaeb5f9f36007127c9aa98d436a80b3cce3fcd56d57c4103fb18f1819d5c238a49b0985fe7b49
e=10001
M=b503be7137293906649e0ae436e29819ea2d06abf31e10091a7383349de84c5b
测试结果

参考文献
张焕国,唐明.密码学引论(第三版).武汉大学出版社,2015年


 浙公网安备 33010602011771号
浙公网安备 33010602011771号