《托马斯微积分》阅读笔记#2

由于又想通了，于是再次开始搞oi
————————————————————————————————————————————————————

斜率

（接上次的增量，本节会常常用到”Δ“。）
每条非垂直的直线都有斜率。
“每行（xing）进单位距离时高度的变化为直线的斜率。
（下图为斜率视图，摘自《托马斯微积分》

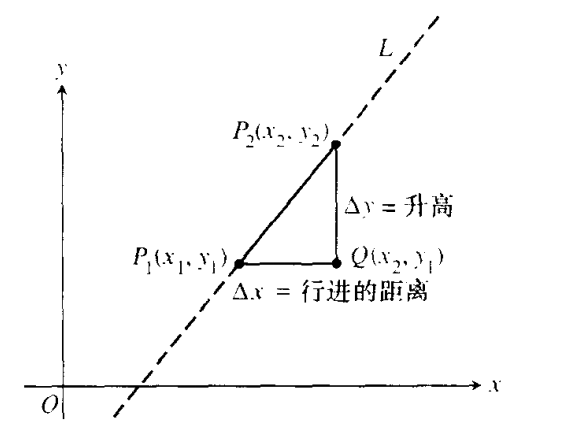
如上图所示，出现了一个直角三角形，其中的P1P2截取与直线L，另两条直角边为Δx和Δy。
我们把Δx叫做行进的距离，Δy叫做升高（如何计算见认识增量）。
数学上一般称某条直线的斜率为m
则直线L的斜率为m=升高/行进的距离=Δy/Δx=y2-y1/x2-x1；

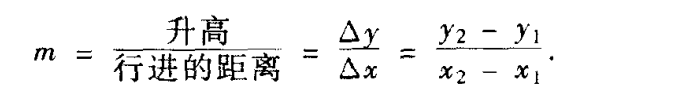
由于垂直直线的Δx=0（于y轴平行），水平方向直线Δy=0，（与x轴平行），所以这里的Δy/Δx没有意义，即看作他们没有斜率。

当x增加时，上升的直线具有正斜率（下图）。图中AB所在直线L的斜率m=2-0/2-0=1；

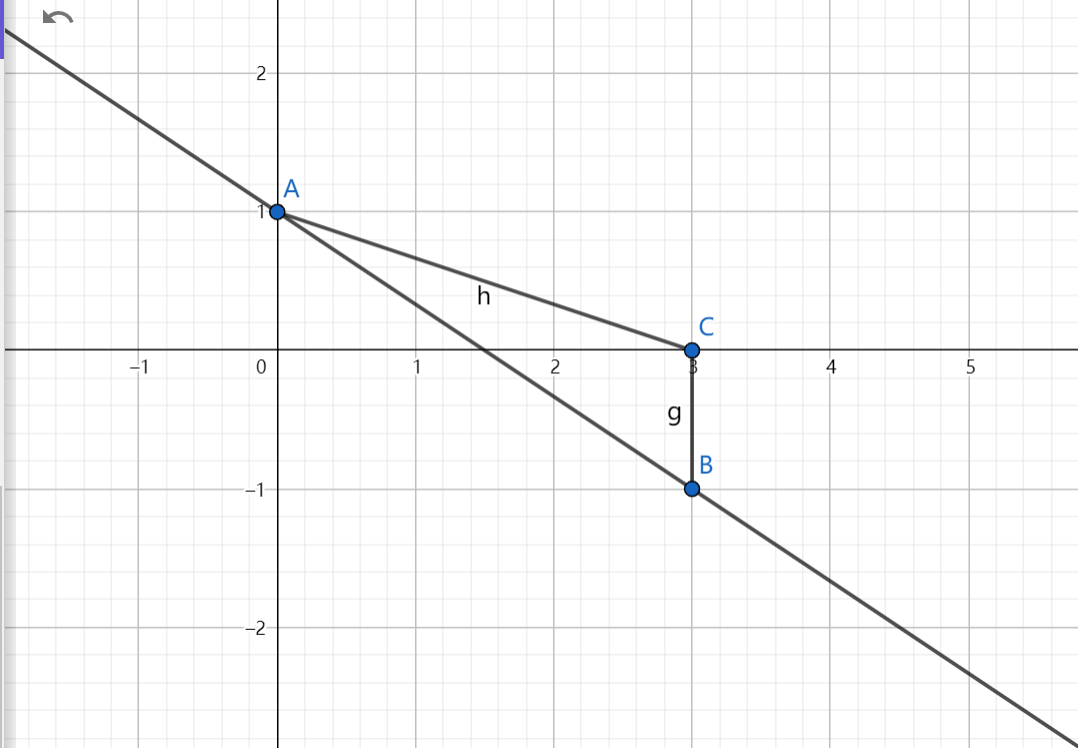
当x增加时，下降的直线具有负斜率（下图）。图中AB所在直线L的斜率m=-1-1/3-0=-2/3.

争取每天一课。