卷积神经网络
卷积神经网络
从全连接层到卷积
全连接神经网络确实可以解决很多问题，但是缺点也是非常明显。首先，当输入的数据比较大时，全连接层需要处理的参数就会变得非常大，比如当传入的图像达到1e6像素时，即使隐藏层只有1000，每一层的连接也会达到1e9的数量级，显然如此巨大数量级的参数计算是不合理的。还有很重要的一点就是全连接层神经网络会失去数据的结构性。
那么很自然的就会引入卷积神经网络这一概念。
卷积神经网络（convolutional neural networks，CNN）是机器学习利用自然图像中一些已知结构的创造性方法。
卷积神经网络正是将空间不变性（spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。
- 平移不变性（translation invariance）：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
- 局部性（locality）：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。
图像卷积
起初，卷积神经网络的设计是为了用于探索图像设计(当然，如今的卷积神经网络不止能处理图像)，所以不妨以图像处理为例。
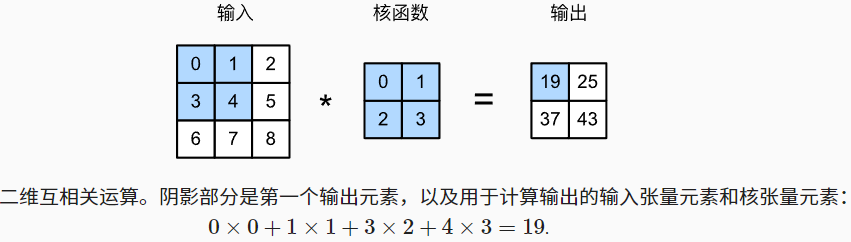
互相关运算
严格来讲，卷积层进行的操作并不是卷积运算，而是互相关运算（cross-correlation）
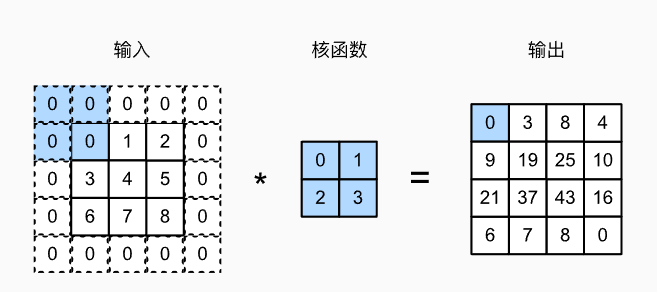
特征映射和感受野
上图中输出的卷积层有时被称为特征映射，因为他可以被视为是下一个输入映射到下一层的空间维度的转换器。
在卷积神经网络中，对于某一层的任意元素x，其感受野是指在向前传播期间可能影响x计算的所有元素（来自所有先前层）。
填充和步幅
填充
假设有以下场景：有时，在应用了连续的卷积之后，我们最终得到的输出远小于输入大小，这会导致原始图像的边界丢失了许多有用的信息。填充是就解决此问题最有效的办法。
填充：在输入图像的边界填充元素（通常是0）。
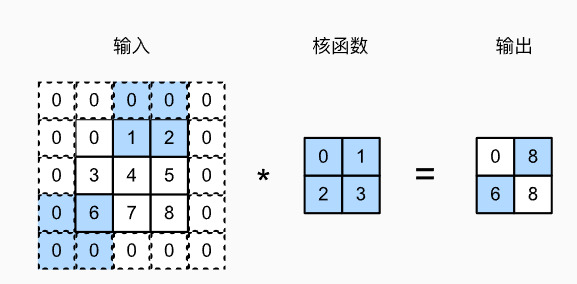
步幅
通常在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动，一般每次滑动一个元素。但是，有时为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。
我们将每次滑动的数量称为步幅。
可以看到，为了计算输出中第一列的第二个元素和第一行的第二个元素，卷积窗口分别向下滑动三行和向右滑动两列。但是，当卷积窗口继续向右滑动两列时，没有输出，因为输入元素无法填充窗口（除非我们添加另一列填充）。
垂直步幅为3，水平步幅为2的二维互相关计算
多输入多输出通道
当我们添加通道时，我们的输入和隐藏的表示都变成了三维张量。例如，每个RGB输入图像具有3×h×w的形状。我们将这个大小为3的轴称为通道（channel）维度。在本节中，我们将更深入地研究具有多输入和多输出通道的卷积核。
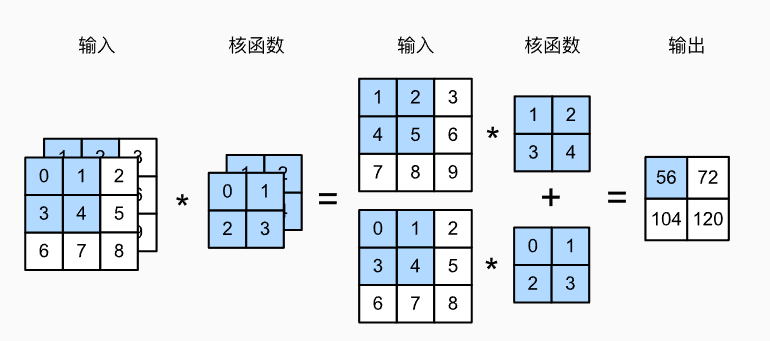
多输入通道
多输出通道
到目前为止，不论有多少输入通道，我们还只有一个输出通道。然而，每一层有多个输出通道是至关重要的。
用\(c_{i}\)和\(c_{0}\)分别表示输入和输出通道的数目，并让\(k_{h}\)和\(k_{w}\)为卷积核的高度和宽度。为了获得多个通道的输出，我们可以为每个输出通道创建一个形状为\(c_{i} \times k_{h} \times k_{w}\)的卷积核，这样的卷积核的形状是\(c_{o} \times c_{i} \times k_{h} \times k_{w}\)。在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的卷积核计算出结果。
汇聚层/池化层
通常当我们处理图像时，我们希望逐渐降低隐藏表示的空间分辨率、聚集信息，这样随着我们在神经网络中层叠的上升，每个神经元对其敏感的感受野（输入）就越大。
而我们的机器学习任务通常会跟全局图像的问题有关（例如，“图像是否包含一只猫呢？”），所以我们最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息，生成越来越粗糙的映射，最终实现学习全局表示的目标，同时将卷积图层的所有优势保留在中间层。
