时序分析:Python 中的 ARIMA 模型
推荐:使用NSDT场景编辑器快速助你搭建可二次编辑的3D应用场景
什么是ARIMA模型?
ARIMA 模型是用于分析和预测时间序列数据的统计模型。ARIMA 方法明确迎合了时间序列中的标准结构,为制作熟练的时间序列预测提供了一种简单而强大的方法。
ARIMA 代表 自回归积分移动平均线。它结合了三个关键方面:
- 自回归 (AR):使用当前观测值和滞后观测值之间相关性的模型。滞后观测值的数量称为滞后顺序或 p。
- 积分(I):使用原始观测值的差分使时间序列平稳。差异运算的次数称为 d。
- 移动平均线 (MA):模型考虑当前观测值与应用于过去观测值的移动平均模型的残差之间的关系。移动平均线窗口的大小是阶数或 q。
ARIMA 模型使用符号 ARIMA(p,d,q) 定义,其中 p、d 和 q 替换为整数值以指定所使用的确切模型。
采用 ARIMA 模型时的关键假设:
- 时间序列是从基础 ARIMA 过程生成的。
- 参数 p、d、q 必须根据原始观测值适当指定。
- 在拟合 ARIMA 模型之前,必须通过差分使时间序列数据变得平稳。
- 残差应不相关,如果模型拟合良好,则正态分布。
总之,ARIMA 模型提供了一种结构化且可配置的方法,用于为预测等目的对时间序列数据进行建模。接下来,我们将研究在 Python 中拟合 ARIMA 模型。
蟒蛇代码示例
在本教程中,我们将使用 Kaggle 的 Netflix 股票数据使用 ARIMA 模型预测 Netflix 股票价格。
数据加载
我们将加载我们的股票价格数据集,并将“日期”列作为索引。
import pandas as pd
net_df = pd.read_csv("Netflix_stock_history.csv", index_col="Date", parse_dates=True)
net_df.head(3)
数据可视化
我们可以使用熊猫“绘图”功能来可视化股票价格和交易量随时间的变化。很明显,股价呈指数级增长。
net_df[["Close","Volume"]].plot(subplots=True, layout=(2,1));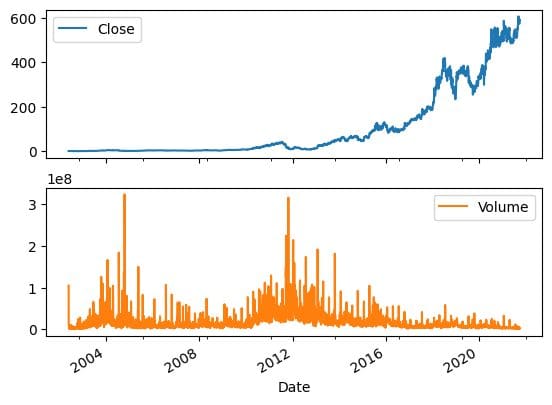
滚动预测 ARIMA 模型
我们的数据集已拆分为训练集和测试集,我们继续训练 ARIMA 模型。然后预测了第一个预测。
通用ARIMA模型的结果很差,因为它产生了一条平线。因此,我们决定尝试滚动预测方法。
注意:代码示例是 BOGDAN IVANYUK 笔记本的修改版本。
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
train_data, test_data = net_df[0:int(len(net_df)*0.9)], net_df[int(len(net_df)*0.9):]
train_arima = train_data['Open']
test_arima = test_data['Open']
history = [x for x in train_arima]
y = test_arima
# make first prediction
predictions = list()
model = ARIMA(history, order=(1,1,0))
model_fit = model.fit()
yhat = model_fit.forecast()[0]
predictions.append(yhat)
history.append(y[0])在处理时间序列数据时,由于依赖于先前的观测值,滚动预测通常是必要的。执行此操作的一种方法是在收到每个新观测值后重新创建模型。
为了跟踪所有观察结果,我们可以手动维护一个名为 history 的列表,该列表最初包含训练数据,每次迭代都会附加新的观察结果。这种方法可以帮助我们获得准确的预测模型。
# rolling forecasts
for i in range(1, len(y)):
# predict
model = ARIMA(history, order=(1,1,0))
model_fit = model.fit()
yhat = model_fit.forecast()[0]
# invert transformed prediction
predictions.append(yhat)
# observation
obs = y[i]
history.append(obs)
模型评估
我们的滚动预测 ARIMA 模型显示,与简单实施相比,改进了 100%,产生了令人印象深刻的结果。
# report performance
mse = mean_squared_error(y, predictions)
print('MSE: '+str(mse))
mae = mean_absolute_error(y, predictions)
print('MAE: '+str(mae))
rmse = math.sqrt(mean_squared_error(y, predictions))
print('RMSE: '+str(rmse))MSE: 116.89611817706545
MAE: 7.690948135967959
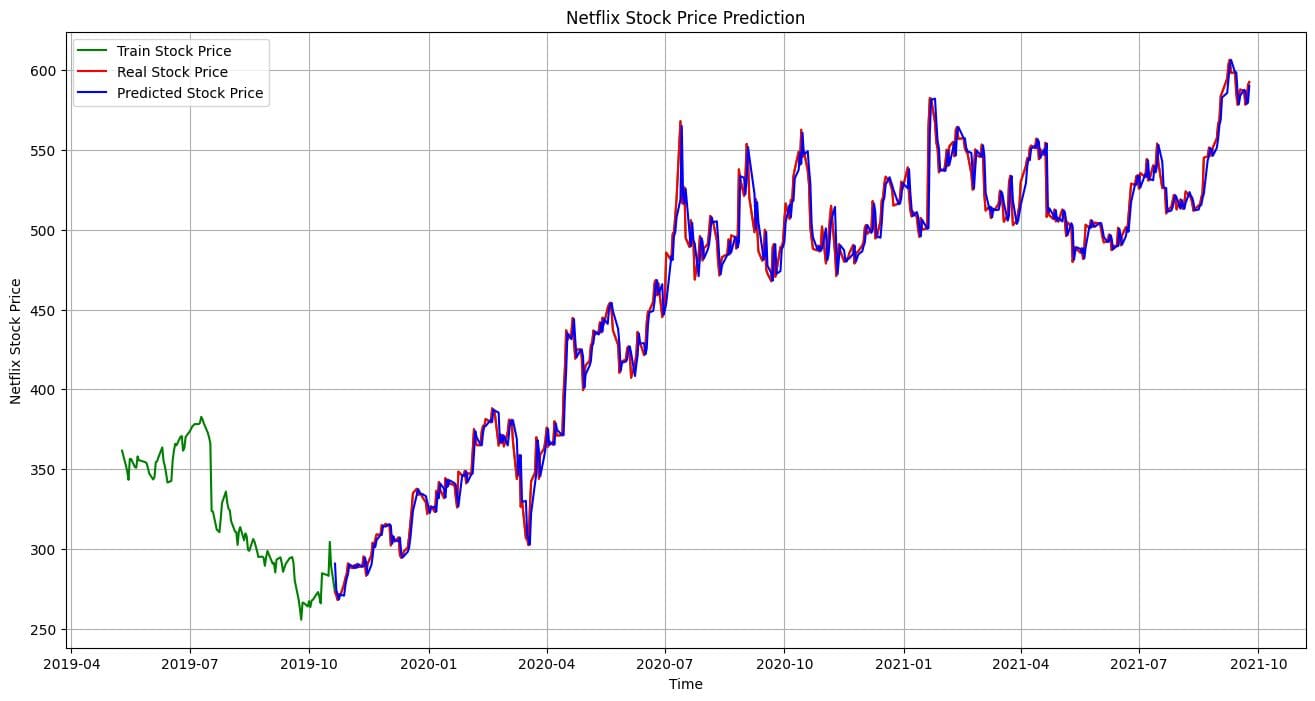
RMSE: 10.811850821069696让我们可视化并将实际结果与预测结果进行比较。很明显,我们的模型已经做出了高度准确的预测。
import matplotlib.pyplot as plt
plt.figure(figsize=(16,8))
plt.plot(net_df.index[-600:], net_df['Open'].tail(600), color='green', label = 'Train Stock Price')
plt.plot(test_data.index, y, color = 'red', label = 'Real Stock Price')
plt.plot(test_data.index, predictions, color = 'blue', label = 'Predicted Stock Price')
plt.title('Netflix Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Netflix Stock Price')
plt.legend()
plt.grid(True)
plt.savefig('arima_model.pdf')
plt.show()
结论
在这个简短的教程中,我们概述了 ARIMA 模型以及如何在 Python 中实现它们以进行时间序列预测。ARIMA 方法提供了一种灵活且结构化的方式来对依赖于先前观测值和过去预测误差的时间序列数据进行建模。如果您对 ARIMA 模型和时间序列分析的全面分析感兴趣,我建议您查看使用时间序列分析进行股票市场预测。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号