面向数据科学家和分析师的统计基础
推荐:使用NSDT场景编辑器助你快速搭建可编辑的3D应用场景
“统计学是科学的语法。卡尔·皮尔逊
统计学在数据科学和数据分析中的重要性不容低估。统计提供了查找结构和提供更深入数据见解的工具和方法。统计学和数学都喜欢事实,讨厌猜测。了解这两个重要主题的基础知识将使您能够批判性地思考,并在使用数据解决业务问题和做出数据驱动的决策时具有创造力。在本文中,我将介绍以下数据科学和数据分析的统计主题:
- Random variables
- Probability distribution functions (PDFs)
- Mean, Variance, Standard Deviation
- Covariance and Correlation
- Bayes Theorem
- Linear Regression and Ordinary Least Squares (OLS)
- Gauss-Markov Theorem
- Parameter properties (Bias, Consistency, Efficiency)
- Confidence intervals
- Hypothesis testing
- Statistical significance
- Type I & Type II Errors
- Statistical tests (Student's t-test, F-test)
- p-value and its limitations
- Inferential Statistics
- Central Limit Theorem & Law of Large Numbers
- Dimensionality reduction techniques (PCA, FA)如果您之前没有统计学知识,并且想从头开始识别和学习基本的统计概念,为您的工作面试做准备,那么本文适合您。对于任何想要刷新他/她的统计知识的人来说,这篇文章也将是一个很好的阅读。
在我们开始之前,欢迎来到LunarTech!
欢迎来到 LunarTech.ai,在这里我们了解求职策略在数据科学和人工智能动态领域的力量。我们深入研究了驾驭竞争激烈的求职过程所需的策略和策略。无论是确定您的职业目标、定制申请材料,还是利用工作委员会和网络,我们的见解都能为您提供找到梦想工作所需的指导。
准备数据科学面试?不要害怕!我们揭示面试过程的复杂性,为您提供必要的知识和准备,以增加成功的机会。从最初的电话筛选到技术评估、技术访谈和行为访谈,我们不遗余力。
在 LunarTech.ai,我们超越了理论。我们是您在技术和数据科学领域取得无与伦比的成功的跳板。我们全面的学习之旅专为无缝融入您的生活方式而量身定制,让您在获得尖端技能的同时,在个人和专业承诺之间取得完美平衡。我们致力于您的职业发展,包括工作安置协助、专家简历制作和面试准备,您将成为行业就绪的强者。
立即加入我们雄心勃勃的个人社区,一起踏上这一激动人心的数据科学之旅。有了 LunarTech.ai,未来是光明的,你掌握着解锁无限机会的钥匙。
随机变量
随机变量的概念构成了许多统计概念的基石。可能很难理解其正式的数学定义,但简单地说,随机变量是一种将随机过程的结果(例如掷硬币或掷骰子)映射到数字的方法。例如,我们可以通过随机变量 X 定义抛硬币的随机过程,如果结果是正面,则取值 1,如果结果是反面,则取值 0。

在这个例子中,我们有一个随机抛硬币的过程,这个实验可以产生两个可能的结果:{0,1}。这组所有可能的结果称为实验的样本空间。每次重复随机过程时,它被称为一个事件。 在此示例中,掷硬币并获得尾巴作为结果是一个事件。该事件发生特定结果的几率或可能性称为该事件的概率。事件的概率是随机变量取特定值x的可能性,该值可以用P(x)描述。在掷硬币的例子中,正面或反面的可能性是相同的,即 0.5% 或 50%。所以我们有以下设置:
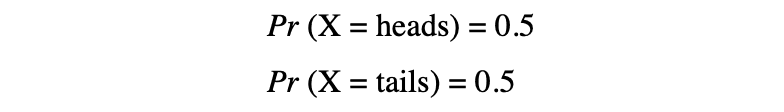
在此示例中,事件的概率只能取 [0,1] 范围内的值。
统计学在数据科学和数据分析中的重要性不容低估。统计提供了查找结构和提供更深入数据见解的工具和方法。
均值、方差、标准差
要理解均值、方差和许多其他统计主题的概念,学习总体和样本的概念非常重要。总体是所有观测值(个体、对象、事件或过程)的集合,通常非常大且多样化,而样本是总体观测值的子集,理想情况下是总体的真实表示。
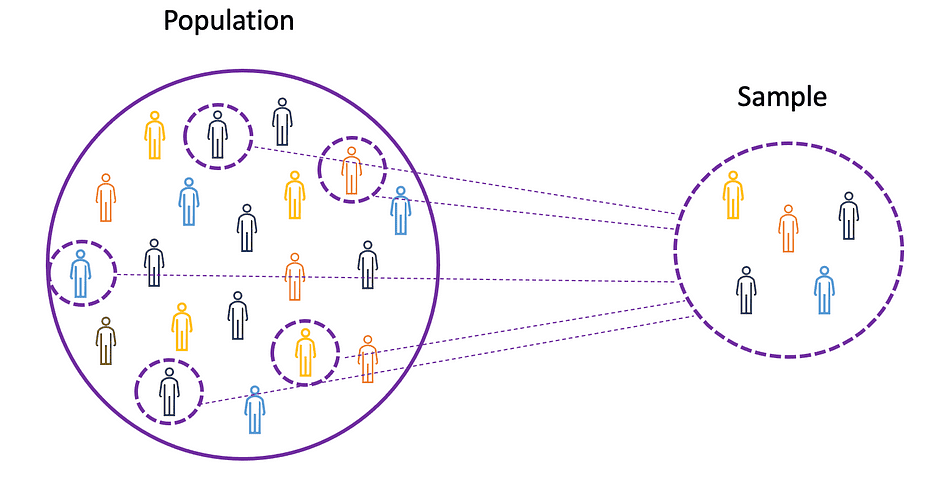
图片来源:作者
鉴于对整个人群进行实验是不可能的,或者只是太昂贵,研究人员或分析师在他们的实验或试验中使用样本而不是整个人群。为了确保实验结果可靠且适用于整个总体,样本需要真实地表示总体。也就是说,样本需要无偏。为此,可以使用统计抽样技术,例如随机抽样、系统抽样、聚类抽样、加权抽样和分层抽样。
意味 着
平均值,也称为平均值,是一组有限数字的中心值。假设数据中的随机变量 X 具有以下值:

其中 N 是样本集中的观测值或数据点的数量,或者只是数据频率。那么由 ?(通常用于近似总体均值)定义的样本均值可以表示如下:
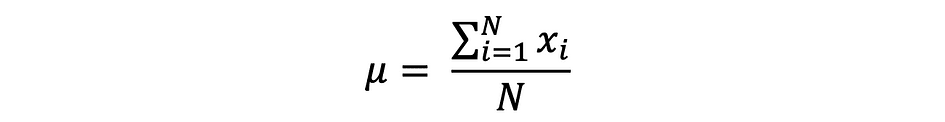
平均值也称为期望值,通常由 E() 或顶部带有条形的随机变量定义。例如,随机变量 X 和 Y(即 E(X) 和 E(Y))的期望可以表示如下:
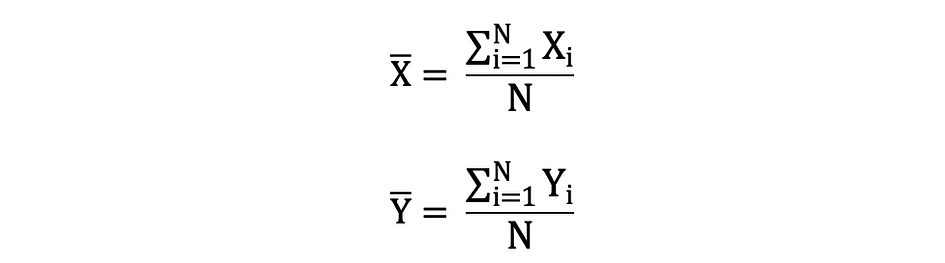
import numpy as np
import math
x = np.array([1,3,5,6])
mean_x = np.mean(x)
# in case the data contains Nan values
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanmean(x_nan)方差
方差衡量数据点与平均值的分布距离,等于数据值与平均值(平均值)之差的平方和。此外,总体方差可以表示如下:

x = np.array([1,3,5,6])
variance_x = np.var(x)
# here you need to specify the degrees of freedom (df) max number of logically independent data points that have freedom to vary
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanvar(x_nan, ddof = 1)要推导不同流行概率分布函数的期望和方差,请查看此 Github 存储库。
标准差
标准差只是方差的平方根,用于衡量数据与其平均值的差异程度。由 sigma 定义的标准差可以表示如下:
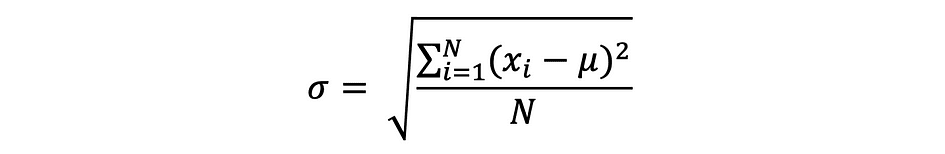
标准差通常优于方差,因为它与数据点具有相同的单位,这意味着您可以更轻松地解释它。
x = np.array([1,3,5,6])
variance_x = np.std(x)
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanstd(x_nan, ddof = 1)协方差
协方差是两个随机变量联合变异性的度量,描述了这两个变量之间的关系。它被定义为两个随机变量与其均值的偏差的乘积的期望值。两个随机变量 X 和 Z 之间的协方差可以用以下表达式描述,其中 E(X) 和 E(Z) 分别表示 X 和 Z 的均值。
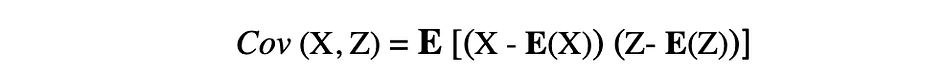
协方差可以取负值或正值以及值 0。协方差的正值表示两个随机变量倾向于在同一方向上变化,而负值表示这些变量在相反的方向上变化。最后,值 0 表示它们不会一起变化。
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
#this will return the covariance matrix of x,y containing x_variance, y_variance on diagonal elements and covariance of x,y
cov_xy = np.cov(x,y)相关
相关性也是关系的度量,它测量两个变量之间线性关系的强度和方向。如果检测到相关性,则意味着两个目标变量的值之间存在关系或模式。两个随机变量 X 和 Z 之间的相关性等于这两个变量之间的协方差除以这些变量的标准差的乘积,可以用以下表达式描述。
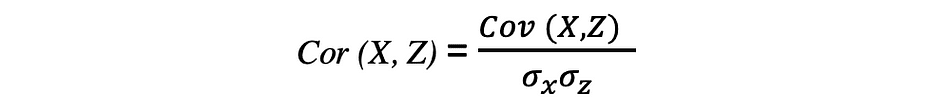
相关系数的值范围介于 -1 和 1 之间。请记住,变量与自身的相关性始终为 1,即 Cor(X, X) = 1。解释相关性时要记住的另一件事是不要将其与因果关系混淆,因为相关性不是因果关系。即使两个变量之间存在相关性,也不能断定一个变量导致另一个变量发生变化。这种关系可能是巧合,或者第三个因素可能导致两个变量发生变化。
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
corr = np.corrcoef(x,y)概率分布函数
描述随机变量在给定范围内(以最小和最大可能值为界)可以采用的所有可能值、样本空间和相应概率的函数称为概率分布函数 (pdf) 或概率密度。每个 pdf 都需要满足以下两个条件:

其中第一个标准声明所有概率都应该是 [0,1] 范围内的数字,第二个标准声明所有可能概率的总和应该等于 1。
概率函数通常分为两类:离散和连续。离散分布函数描述了具有可数样本空间的随机过程,例如抛硬币的例子只有两种可能的结果。连续分布函数描述了具有连续样本空间的随机过程。离散分布函数的例子有伯努利、二项式、泊松、离散均匀。连续分布函数的示例包括正态分布函数、连续均匀分布函数、柯西分布函数。
二项分布
二项分布是 n 个独立实验序列中成功次数的离散概率分布,每个实验都有布尔值结果:成功(概率为 p)或失败(概率 q = 1 ? p)。假设随机变量 X 服从二项分布,那么在 n 个独立试验中观察到 k 个成功的概率可以用以下概率密度函数表示:
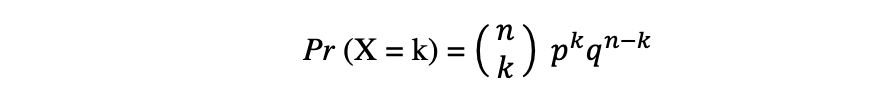
在分析重复独立实验的结果时,二项分布很有用,特别是如果对给定特定错误率达到特定阈值的概率感兴趣。
二项分布均值和方差
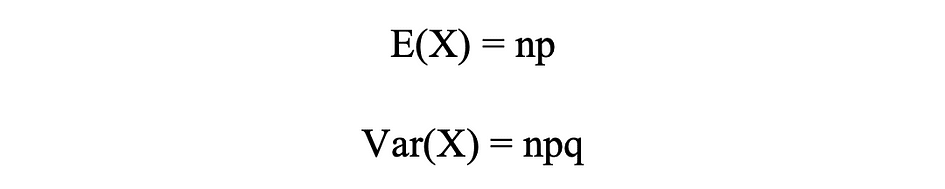
下图可视化了二项分布的示例,其中独立试验的数量等于 8,每个试验的成功概率等于 16%。
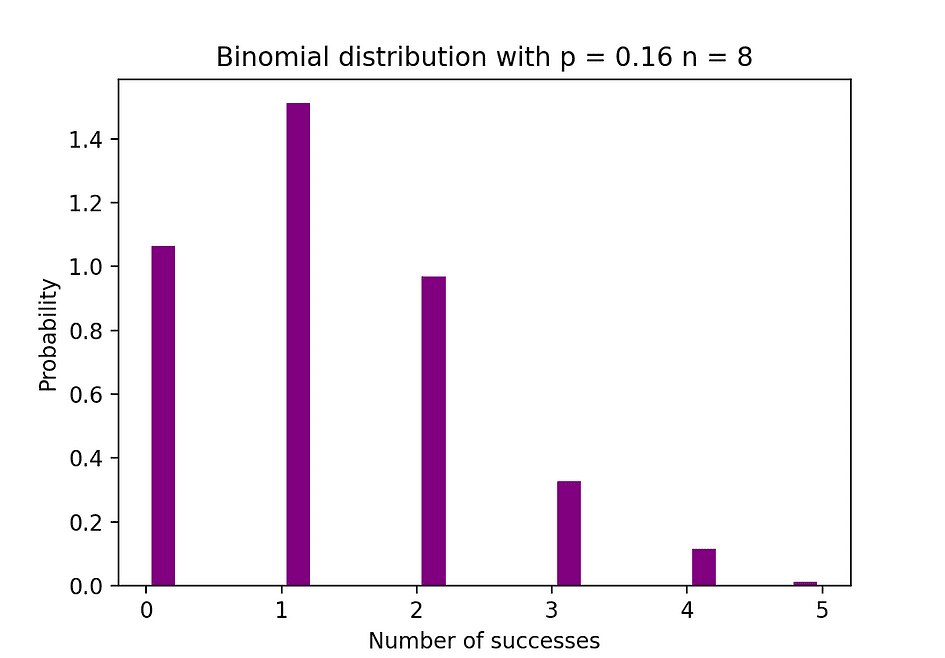
图片来源:作者
# Random Generation of 1000 independent Binomial samples
import numpy as np
n = 8
p = 0.16
N = 1000
X = np.random.binomial(n,p,N)
# Histogram of Binomial distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 20, density = True, rwidth = 0.7, color = 'purple')
plt.title("Binomial distribution with p = 0.16 n = 8")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()泊松分布
泊松分布是给定事件在该时间段内发生的平均次数的离散概率分布。假设随机变量 X 服从泊松分布,那么在一段时间内观察到 k 个事件的概率可以用以下概率函数表示:
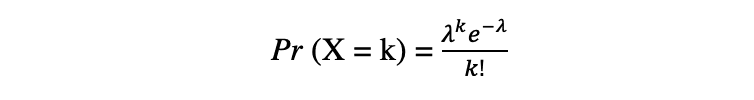
其中 e 是欧拉数和 ? λ,到达率参数是 X 的期望值.泊松分布函数在建模给定时间间隔内发生的可数事件时非常流行。
泊松分布均值和方差

例如,泊松分布可用于对晚上 7 点到 10 点之间到达商店的客户数量或晚上 11 点到 12 点之间到达急诊室的患者数量进行建模。下图可视化了泊松分布的示例,其中我们计算到达网站的 Web 访问者数量,其中假定到达率 lambda 等于 7 分钟。
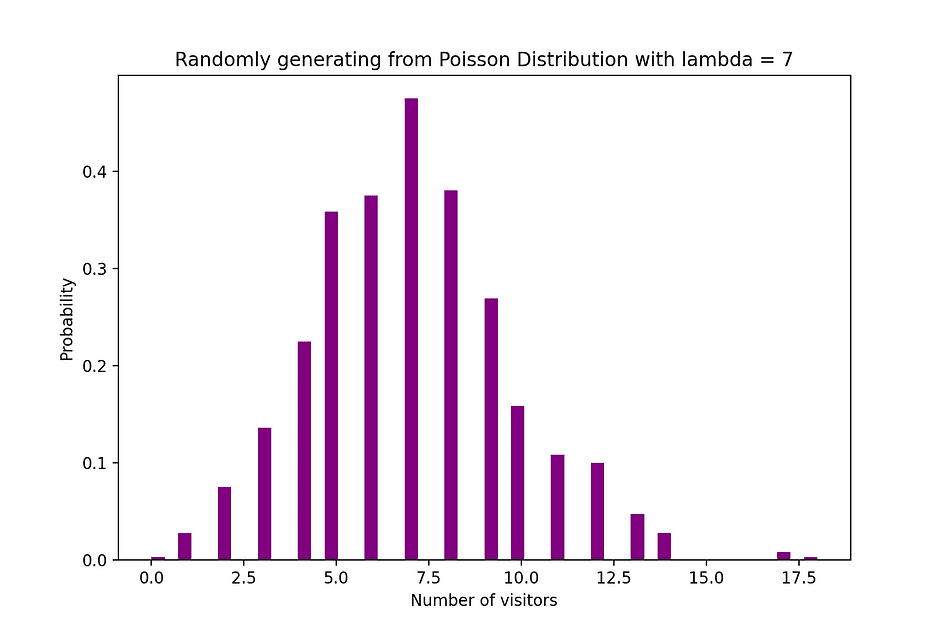
图片来源:作者
# Random Generation of 1000 independent Poisson samples
import numpy as np
lambda_ = 7
N = 1000
X = np.random.poisson(lambda_,N)
# Histogram of Poisson distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 50, density = True, color = 'purple')
plt.title("Randomly generating from Poisson Distribution with lambda = 7")
plt.xlabel("Number of visitors")
plt.ylabel("Probability")
plt.show()正态分布
正态概率分布是实值随机变量的连续概率分布。正态分布,也称为高斯分布,可以说是社会和自然科学中通常用于建模目的的最流行的分布函数之一,例如,它用于对人的身高或考试分数进行建模。假设随机变量 X 服从正态分布,那么它的概率密度函数可以表示如下。
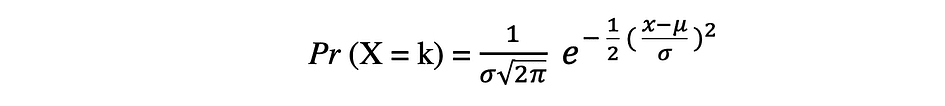
其中参数 ? (亩) 分布的均值是否也称为位置参数、参数? (西格玛) 是分布的标准差,也称为刻度参数。数字?(pi)是一个数学常数,大约等于3.14。
正态分布均值和方差
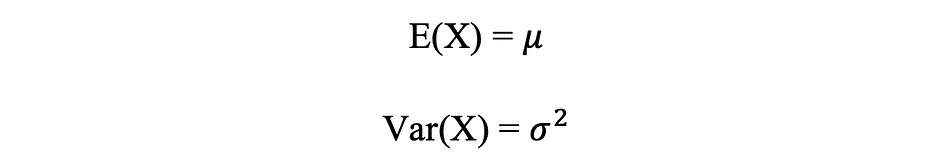
下图可视化了一个正态分布示例,平均值为 0 (? = 0),标准差为 1 (? = 1),称为对称标准正态分布。
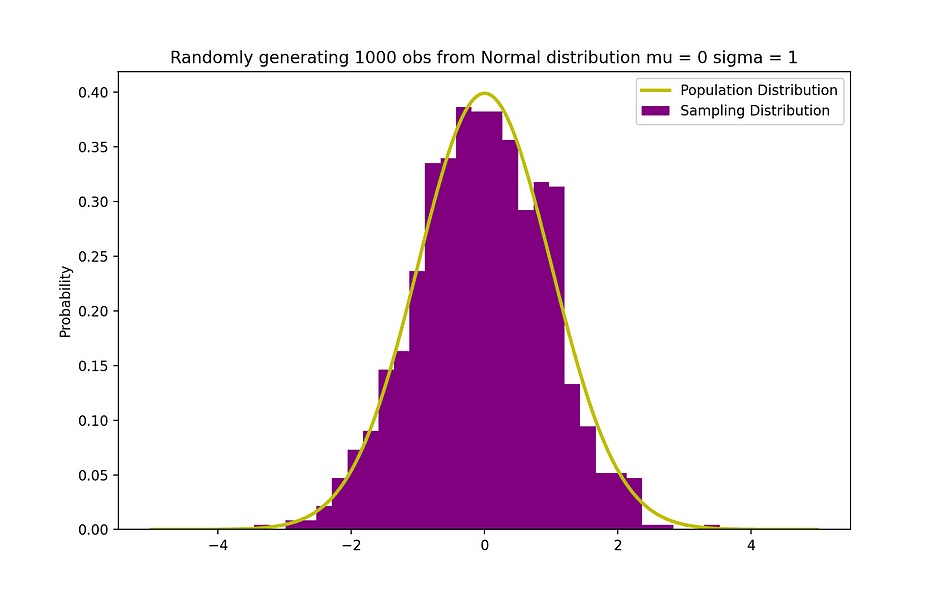
图片来源:作者
# Random Generation of 1000 independent Normal samples
import numpy as np
mu = 0
sigma = 1
N = 1000
X = np.random.normal(mu,sigma,N)
# Population distribution
from scipy.stats import norm
x_values = np.arange(-5,5,0.01)
y_values = norm.pdf(x_values)
#Sample histogram with Population distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 30, density = True,color = 'purple',label = 'Sampling Distribution')
plt.plot(x_values,y_values, color = 'y',linewidth = 2.5,label = 'Population Distribution')
plt.title("Randomly generating 1000 obs from Normal distribution mu = 0 sigma = 1")
plt.ylabel("Probability")
plt.legend()
plt.show()贝叶斯定理
贝叶斯定理或通常称为贝叶斯定律可以说是最强大的概率和统计规则,以英国著名统计学家和哲学家托马斯贝叶斯的名字命名。

图片来源:维基百科
贝叶斯定理是一个强大的概率定律,它将主观性的概念带入了统计和数学的世界,在那里一切都与事实有关。它根据可能与该事件相关的条件的先验信息描述事件的概率。例如,如果已知感染冠状病毒或Covid-19的风险随着年龄的增长而增加,那么贝叶斯定理允许通过年龄条件更准确地确定已知年龄的个体的风险,而不是简单地假设这个个体是整个人群的共同点。
条件概率的概念在贝叶斯理论中起着核心作用,它是在另一个事件已经发生的情况下,一个事件发生的概率的度量。贝叶斯定理可以用以下表达式来描述,其中 X 和 Y 分别代表事件 X 和 Y:

- Pr (X|Y):假设事件或条件 Y 已经发生或为真,事件 X 发生的概率
- Pr (Y|X):假设事件或条件 X 已经发生或为真,事件 Y 发生的概率
- Pr(X)和Pr(Y):分别观测事件X和Y的概率
在前面的例子中,以达到特定年龄为条件感染冠状病毒(事件 X)的概率为 Pr (X|Y),这等于在某个年龄感染冠状病毒的情况下获得冠状病毒的概率,Pr (Y| X),乘以感染冠状病毒的概率Pr(X),除以处于特定年龄的概率Pr(Y)。
线性回归
早些时候,引入了变量之间因果关系的概念,当一个变量对另一个变量产生直接影响时,就会发生这种情况。当两个变量之间的关系是线性的时,线性回归是一种统计方法,可以帮助模拟变量(自变量)中的单位变化对另一个变量(因变量)的值的影响。
因变量通常称为响应变量或解释变量,而自变量通常称为回归变量或解释变量。当线性回归模型基于单个自变量时,该模型称为简单线性回归,当模型基于多个自变量时,它称为多元线性回归。 简单线性回归可以用以下表达式来描述:

其中 Y 是因变量,X 是作为数据一部分的自变量,?0 是未知且常数的截距,?1 是斜率系数或对应于未知且常数的变量 X 的参数。最后,u 是模型在估计 Y 值时产生的误差项。线性回归背后的主要思想是通过一组配对(X,Y)数据找到最拟合的直线,回归线。线性回归应用程序的一个示例是模拟鳍状肢长度对企鹅体重的影响,如下所示。

图片来源:作者
# R code for the graph
install.packages("ggplot2")
install.packages("palmerpenguins")
library(palmerpenguins)
library(ggplot2)
View(data(penguins))
ggplot(data = penguins, aes(x = flipper_length_mm,y = body_mass_g))+
geom_smooth(method = "lm", se = FALSE, color = 'purple')+
geom_point()+
labs(x="Flipper Length (mm)",y="Body Mass (g)")具有三个自变量的多元线性回归可以用以下表达式描述:
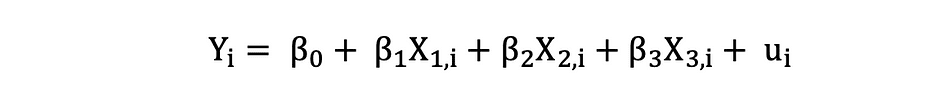
普通最小二乘法
普通最小二乘法 (OLS) 是一种在线性回归模型中估计未知参数(如 ?0 和 ?1)的方法。该模型基于最小二乘原理,该原理最小化观测因变量与其由自变量的线性函数预测的值(通常称为拟合值)之间的差值的平方和。因变量 Y 的实际值和预测值之间的这种差异称为残差,OLS 的作用是最小化残差平方和。此优化问题导致未知参数 ?0 和 ?1 的以下 OLS 估计值,这些参数也称为系数估计值。
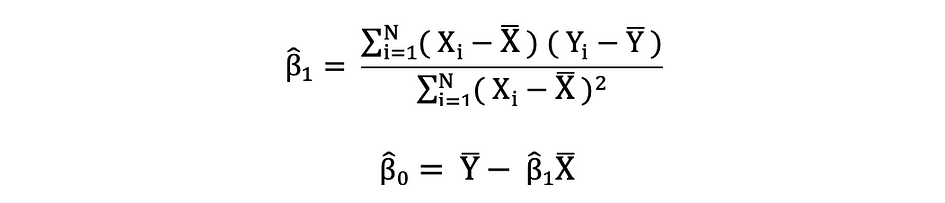
估计简单线性回归模型的这些参数后,响应变量的拟合值可以按如下方式计算:
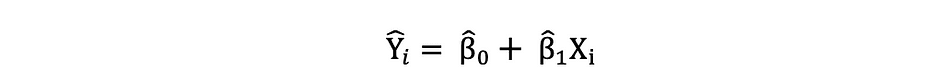
标准误差
残差或估计误差项可按如下方式确定:
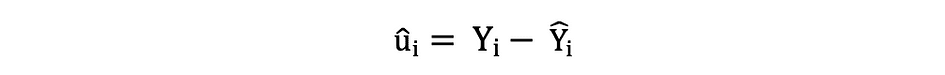
请务必记住误差项和残差之间的差异。从不观察误差项,而残差是根据数据计算的。OLS 估计每个观测值的误差项,但不估计实际误差项。因此,真正的误差方差仍然未知。此外,这些估计数受到抽样不确定性的影响。这意味着我们将永远无法从经验应用中的样本数据中确定这些参数的确切估计值,即真实值。但是,我们可以通过使用残差计算样本残差来估计它,如下所示。
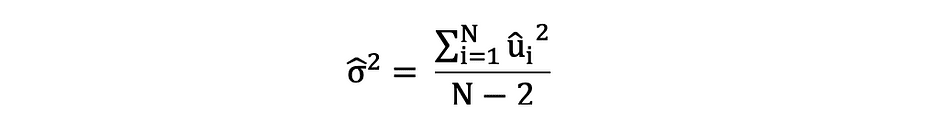
此样本残差方差估计值有助于估计估计参数的方差,通常表示如下:
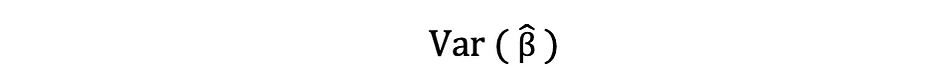
此方差项的平方根称为估计值的标准误,它是评估参数估计值准确性的关键组成部分。它用于计算测试统计量和置信区间。标准误差可以表示如下:
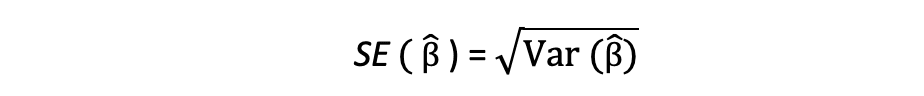
请务必记住误差项和残差之间的差异。从不观察误差项,而残差是根据数据计算的。
OLS 假设
OLS估计方法做出以下假设,需要满足这些假设才能获得可靠的预测结果:
A1:线性假设表明模型在参数上是线性的。
A2:随机样本假设指出样本中的所有观测值都是随机选择的。
A3:外生性假设指出自变量与误差项不相关。
A4:同斜度假设指出所有误差项的方差是恒定的。
A5:没有完美的多重共线性假设指出,没有一个自变量是恒定的,并且自变量之间没有精确的线性关系。
def runOLS(Y,X):
# OLS esyimation Y = Xb + e --> beta_hat = (X'X)^-1(X'Y)
beta_hat = np.dot(np.linalg.inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y))
# OLS prediction
Y_hat = np.dot(X,beta_hat)
residuals = Y-Y_hat
RSS = np.sum(np.square(residuals))
sigma_squared_hat = RSS/(N-2)
TSS = np.sum(np.square(Y-np.repeat(Y.mean(),len(Y))))
MSE = sigma_squared_hat
RMSE = np.sqrt(MSE)
R_squared = (TSS-RSS)/TSS
# Standard error of estimates:square root of estimate's variance
var_beta_hat = np.linalg.inv(np.dot(np.transpose(X),X))*sigma_squared_hat
SE = []
t_stats = []
p_values = []
CI_s = []
for i in range(len(beta)):
#standard errors
SE_i = np.sqrt(var_beta_hat[i,i])
SE.append(np.round(SE_i,3))
#t-statistics
t_stat = np.round(beta_hat[i,0]/SE_i,3)
t_stats.append(t_stat)
#p-value of t-stat p[|t_stat| >= t-treshhold two sided]
p_value = t.sf(np.abs(t_stat),N-2) * 2
p_values.append(np.round(p_value,3))
#Confidence intervals = beta_hat -+ margin_of_error
t_critical = t.ppf(q =1-0.05/2, df = N-2)
margin_of_error = t_critical*SE_i
CI = [np.round(beta_hat[i,0]-margin_of_error,3), np.round(beta_hat[i,0]+margin_of_error,3)]
CI_s.append(CI)
return(beta_hat, SE, t_stats, p_values,CI_s,
MSE, RMSE, R_squared)参数属性
在满足 OLS 标准 A1 — A5 的假设下,系数 β0 和 β1 的 OLS 估计量为 BLUE 且一致。
高斯-马尔可夫定理
该定理突出了 OLS 估计的性质,其中术语 BLUE 代表最佳线性无偏估计器。
偏见
估计器的偏差是其期望值与被估计参数的真实值之间的差值,可以表示如下:
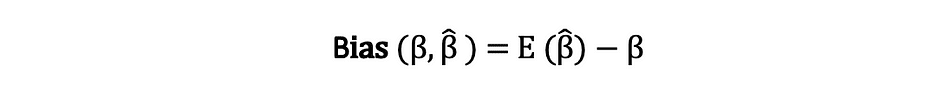
当我们声明估计器是无偏的时,我们的意思是偏差等于零,这意味着估计器的期望值等于真实参数值,即:

无偏性不能保证任何特定样本获得的估计值等于或接近?。这意味着,如果从总体中反复抽取随机样本,然后每次计算估计值,那么这些估计值的平均值将等于或非常接近β。
效率
高斯-马尔可夫定理中的“最佳”一词与估计量的方差有关,称为效率。 一个参数可以有多个估计量,但方差最小的估计量称为有效估计量。
一致性
术语一致性与术语样本大小和收敛性齐头并进。如果当样本量变得非常大时,估计器收敛到真实参数,则称此估计器是一致的,即:

在满足 OLS 标准 A1 — A5 的假设下,系数 β0 和 β1 的 OLS 估计量为 BLUE 且一致。
高斯-马尔可夫定理
所有这些性质都适用于高斯-马尔可夫定理中总结的OLS估计。换句话说,OLS 估计具有最小的方差,它们是无偏的,参数是线性的,并且是一致的。这些属性可以通过使用前面的 OLS 假设进行数学证明。
置信区间
置信区间是包含具有特定预先指定概率的真实总体参数的范围,称为实验的置信水平,它是通过使用样本结果和边际误差获得的。
误差幅度
边际误差是样本结果之间的差异,并且基于如果使用整个总体的结果。
置信水平
置信水平描述了实验结果的确定性水平。例如,95%的置信水平意味着,如果重复执行相同的实验100次,那么这95次试验中的100次将产生类似的结果。请注意,置信水平是在实验开始之前定义的,因为它会影响实验结束时的误差幅度。
OLS 估计值的置信区间
如前所述,简单线性回归的 OLS 估计值、截距 ?0 和斜率系数 ?1 的估计值受到采样不确定性的影响。但是,我们可以为这些参数构建置信区间,它将在所有样本的 95% 中包含这些参数的真实值。也就是说,95% 置信区间 ?可以解释如下:
- 置信区间是假设检验不能被否定到 5% 水平的值集。
- 置信区间有 95% 的机会包含真实值 ?。
OLS 估计值的 95% 置信区间可以构造如下:

它基于参数估计值、该估计值的标准误差以及表示对应于 1% 拒绝规则的边际误差的值 96.5。此值是使用正态分布表确定的,本文稍后将对此进行讨论。同时,下图说明了95%置信区间的概念:
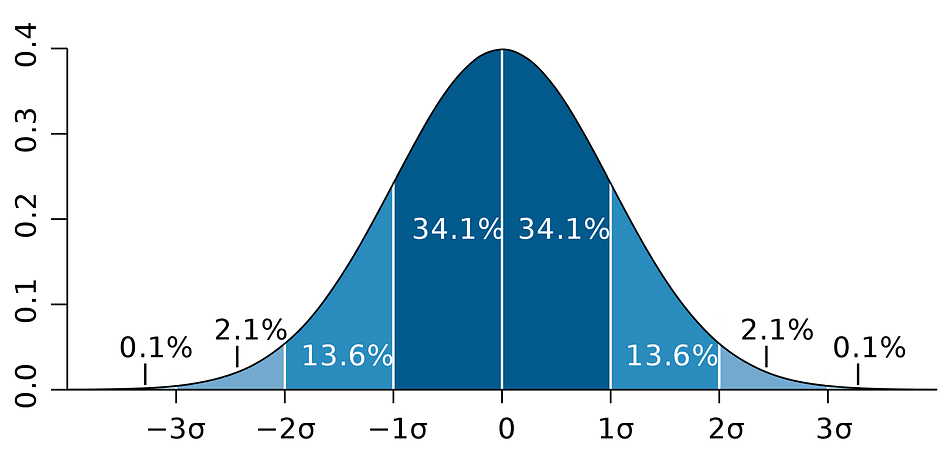
图片来源:维基百科
请注意,置信区间也取决于样本数量,因为它是使用基于样本数量的标准误差计算的。
置信水平是在实验开始之前定义的,因为它会影响实验结束时的误差幅度。
统计假设检验
在统计学中检验假设是一种测试实验或调查结果以确定结果的意义的方法。基本上,人们通过计算结果偶然发生的几率来测试获得的结果是否有效。如果是字母,那么结果不可靠,实验也不可靠。假设检验是统计推断的一部分。
零假设和备择假设
首先,您需要确定要检验的论文,然后您需要制定零假设和备择假设。 该检验可以有两种可能的结果,根据统计结果,您可以拒绝或接受所述假设。根据经验,统计学家倾向于将假设的版本或表述置于需要拒绝的零假设下,而可接受的和期望的版本则在备择假设下陈述。
统计显著性
让我们看一下前面提到的示例,其中线性回归模型用于调查企鹅的自变量鳍状肢长度是否对因变量身体质量产生影响。我们可以用下面的统计表达式来表述这个模型:

然后,一旦估计了系数的 OLS 估计值,我们就可以制定以下零假设和备择假设来检验鳍状肢长度是否对体重有统计上的显着影响:
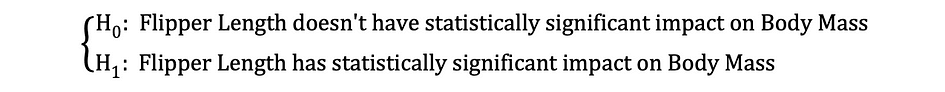
其中 H0 和 H1 分别表示原假设和备择假设。拒绝原假设意味着鳍状肢长度增加一个单位会对体重产生直接影响。假设参数估计值 ?1 描述了自变量鳍状肢长度对因变量 Body Mass 的这种影响。这个假设可以重新表述如下:

其中 H0 表示参数估计值 ?1 等于 0,即鳍状肢长度对体重的影响在统计上不显著,而 H0 表示参数估计值 ?1 不等于 0,表明鳍状肢长度对体重的影响在统计上显著。
类型 I 和类型 II 错误
在执行统计假设检验时,需要考虑两种概念类型的误差:类型 I 错误和类型 II 错误。当错误地拒绝 Null 时,会发生类型 I 错误,而当错误地未拒绝 Null 假设时,会发生类型 II 错误。混淆矩阵可以帮助清楚地可视化这两种类型的错误的严重性。
根据经验,统计学家倾向于将假设的版本置于需要拒绝的零假设下,而可接受的和期望的版本则在备择假设下陈述。
统计检验
陈述 Null 和备择假设并定义检验假设后,下一步是确定哪个统计检验是合适的并计算检验统计量。是否拒绝 Null 可以通过将检验统计量与临界值进行比较来确定。此比较显示观测检验统计量是否比定义的临界值更极端,并且可以产生两种可能的结果:
- 检验统计量比临界值更极端?原假设可以被否定
- 检验统计量不如临界值极端?不能否定原假设
临界值基于预先指定的显著性水平 ?(通常选择等于 5%)和检验统计量遵循的概率分布类型。临界值将该概率分布曲线下的面积划分为拒绝区域和非拒绝区域。有许多统计检验用于检验各种假设。统计检验的例子有学生t检验、F检验、卡方检验、德宾-豪斯曼-吴内生性检验、W海特异方差检验。在本文中,我们将研究其中两个统计测试。
当错误地拒绝 Null 时,会发生类型 I 错误,而当错误地未拒绝 Null 假设时,会发生类型 II 错误。
学生的t检验
最简单和最受欢迎的统计检验之一是学生 t 检验。可用于测试各种假设,尤其是在处理假设时,其中主要感兴趣的领域是找到单个变量的统计显着效应的证据。 t 检验的检验统计量服从学生的 t 分布,可按如下方式确定:

其中,提名器中的 h0 是测试参数估计值所依据的值。因此,t 检验统计量等于参数估计值减去假设值除以系数估计值的标准误。在前面所述的假设中,我们想测试鳍状肢长度是否对体重有统计学意义的影响。可以使用 t 检验执行此检验,在这种情况下,h0 等于 0,因为斜率系数估计值是针对值 0 检验的。
t 检验有两个版本:双侧 t 检验和单侧 t 检验。 是否需要前一个版本或后一个版本的检验完全取决于要检验的假设。
当假设在类似于以下示例的原假设和备择假设下检验相等与不相等关系时,可以使用双侧 或双尾 t 检验:
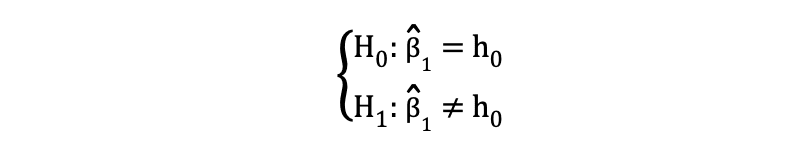
双侧 t 检验有两个排斥区域,如下图所示:

图片来源:Hartmann,K.,Krois,J.,Waske,B.(2018):电子学习项目SOGA:统计和地理空间数据分析。柏林自由大学地球科学系
在此版本的 t 检验中,如果计算的 t 统计量太小或太大,则拒绝 Null。
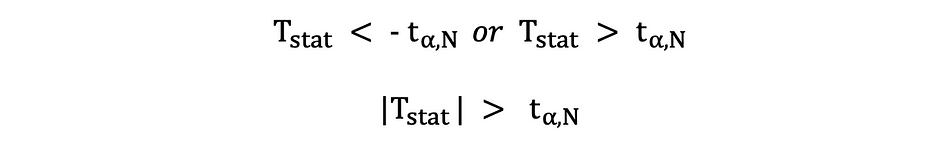
在这里,根据样本数量和所选显著性水平将检验统计量与临界值进行比较。要确定截止点的确切值,可以使用双侧 t 分布表。
当假设在原假设和备择假设下检验正/负与负/正关系时,可以使用单侧或单尾 t 检验,类似于以下示例:
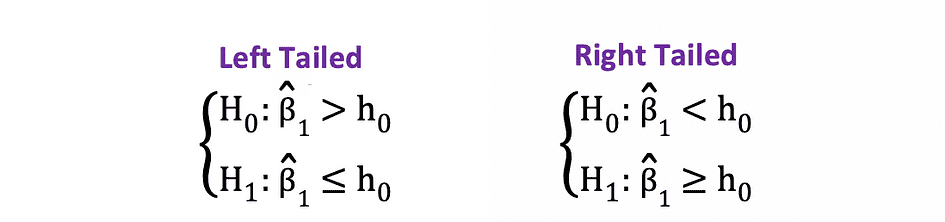
单侧 t 检验具有单个拒绝区域,根据假设侧,拒绝区域位于左侧或右侧,如下图所示:

图片来源:Hartmann,K.,Krois,J.,Waske,B.(2018):电子学习项目SOGA:统计和地理空间数据分析。柏林自由大学地球科学系
在此版本的 t 检验中,如果计算的 t 统计量小于/大于临界值,则拒绝 Null。

F 检验
F检验是另一种非常流行的统计检验,通常用于检验检验多个变量的联合统计显著性的假设。 当您要测试多个自变量是否对因变量具有统计显著影响时,就是这种情况。下面是可以使用 F 检验检验的统计假设的示例:
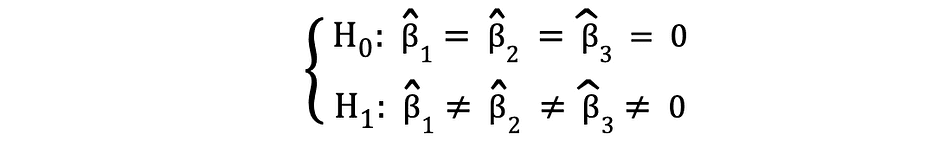
其中 Null 表示对应于这些系数的三个变量在统计意义上共同不显著,而备择表示这三个变量在统计意义上共同显著。F 检验的检验统计量服从 F 分布,可以按如下方式确定:

其中 SSR受限是受限 模型的残差平方和,该模型是同一模型,从数据中排除在 Null 下声明为不重要的目标变量,SSRunrestricted 是非受限模型的残差平方和这是包含所有变量的模型,q 表示在 Null 下联合检验无显著性的变量数,N 是样本数量,k 是无限制模型中变量的总数。运行 OLS 回归后,SSR 值在参数估计值旁边提供,F 统计量也是如此。下面是标记了 SSR 和 F 统计值的 MLR 模型输出示例。
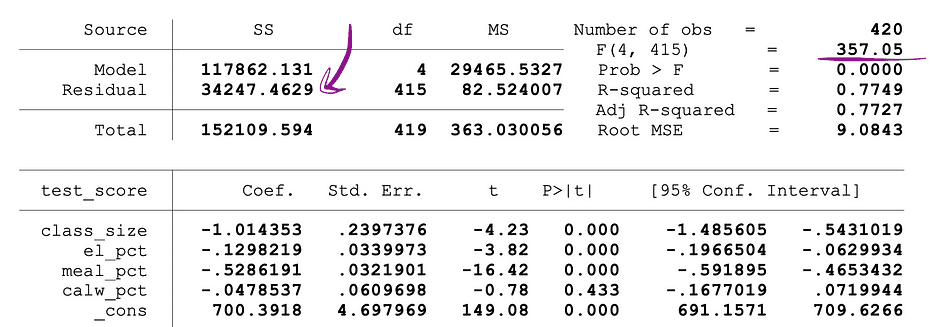
图片来源:Stock and Whatson
F 检验具有单个排斥区域,如下所示:
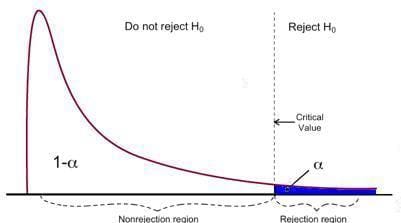
图片来源:密歇根大学
如果计算出的 F 统计量大于临界值,则可以拒绝 Null,这表明自变量在统计意义上共同显著。拒绝规则可以表示如下:
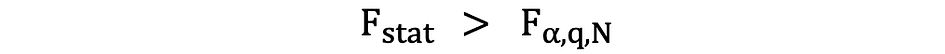
P 值
确定是否定或支持原假设的另一种快速方法是使用 p 值。p 值是 Null 下条件发生的概率。换个说法,p 值是假设原假设为真,观察到结果至少与检验统计量一样极端的概率。p 值越小,反对原假设的证据越强,表明它可以被否定。
p 值的解释取决于所选的显著性水平。大多数情况下,1%、5% 或 10% 的显著性水平用于解释 p 值。因此,这些检验统计量的 p 值可用于检验相同的假设,而不是使用 t 检验和 F 检验。
下图显示了具有两个自变量的 OLS 回归的示例输出。在此表中,t 检验的 p 值(检验class_size变量参数估计值的统计显著性)和 F 检验的 p 值(检验class_size的联合统计显著性)和el_pct变量参数估计值下划线。
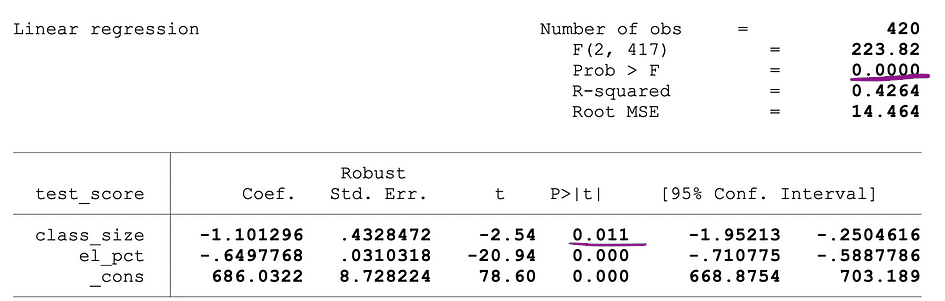
图片来源:Stock and Whatson
对应于class_size变量的 p 值为 0.011,将此值与显著性水平 1% 或 0.01、5% 或 0.05、10% 或 0.1 进行比较时,可以得出以下结论:
- 0.011 > 0.01 ?在 1% 显著性水平下不能否定 t 检验的空值
- 0.011 < 0.05 ?在 5% 显著性水平下,t 检验的空可以被拒绝
- 0.011 < 0.10 ?在 10% 显著性水平下,可以否定 t 检验的空
因此,此 p 值表明class_size变量的系数在 5% 和 10% 显著性水平下具有统计显著性。对应于 F 检验的 p 值为 0.0000,并且由于 0 小于所有三个临界值;0.01, 0.05, 0.10,我们可以得出结论,在所有三种情况下,F 检验的 Null 都可以被拒绝。这表明class_size变量和el_pct变量的系数在 1%、5% 和 10% 显著性水平上具有共同统计显著性。
p 值的限制
虽然,使用 p 值有很多好处,但它也有局限性。 也就是说,p 值取决于关联量级和样本数量。如果效应的量级较小且在统计意义上不显著,则 p 值可能仍显示显著影响,因为大样本数量很大。反之亦然,效应可能很大,但如果样本量较小,则无法满足 p<0.01、0.05 或 0.10 标准。
推论统计
推论统计使用样本数据对样本数据来源的总体做出合理的判断。它用于调查样本中变量之间的关系,并预测这些变量与更大总体的关系。
大数定律(LLN)和中心极限定理(CLM)在推论统计中都起着重要作用,因为它们表明,当数据足够大时,无论原始总体分布的形状如何,实验结果都成立。收集的数据越多,统计推断就越准确,因此生成的参数估计值就越准确。
大数定律 (LLN)
假设 X1, X2, . . . , Xn 都是具有相同底层分布的独立随机变量,也称为独立相同分布或 i.i.d,其中所有 X 都具有相同的平均值 ? 和标准差 ?。随着样本数量的增加,所有 X 的平均值等于平均值的概率 ?等于 1。大数定律可以概括如下:
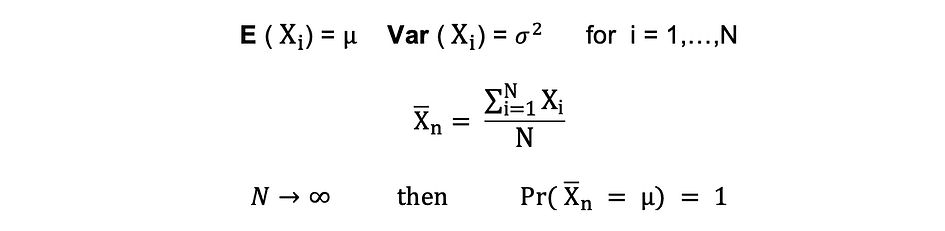
中心极限定理 (CLM)
假设 X1, X2, . . . , Xn 都是具有相同底层分布的独立随机变量,也称为独立相同分布或 i.i.d,其中所有 X 都具有相同的平均值 ? 和标准差 ?。随着样本数量的增加,X 的概率分布收敛于正态分布中的均值 ? 和方差?平方。中心极限定理可以总结如下:
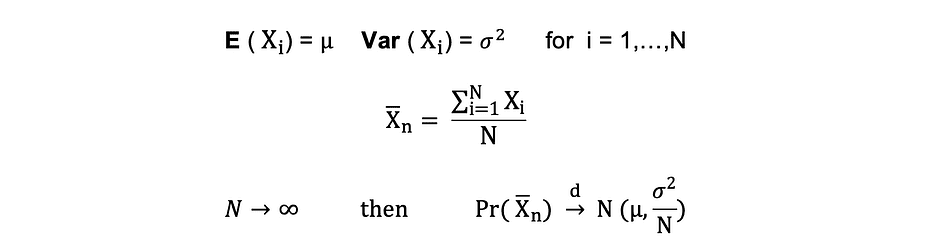
换句话说,当你有一个有平均值的人口时?和标准差 ?并且您从该总体中抽取足够大的随机样本并进行替换,则样本均值的分布将近似正态分布。
降维技术
降维是将数据从高维空间转换为低维空间,使得数据的这种低维表示仍然尽可能多地包含原始数据的有意义属性。
随着大数据的日益普及,对这些降维技术的需求也随之增加,减少了不必要的数据和特征的数量。流行的降维技术的例子包括主成分分析、因子分析、典型相关、随机森林。
主成分分析
主成分分析或PCA是一种降维技术,通常用于降低大型数据集的维数,方法是将大量变量转换为仍包含原始大型数据集中大部分信息或变体的较小数据集。
假设我们有一个带有 p 个变量的数据 X;X1, X2, ...., Xp 与特征向量 e1, ..., ep, 和特征值 ?1,..., ?p.特征值显示特定数据字段在总方差中解释的方差。PCA背后的想法是创建新的(自变量)变量,称为主成分,它们是现有变量的线性组合。第 i个主成分可以表示如下:

然后,使用肘部规则或 Kaiser 规则,您可以确定在不丢失太多信息的情况下以最佳方式汇总数据的主分量的数量。查看每个主成分解释的总变异比例(PRTV)也很重要,以确定包括或排除它是否有益。第i个主成分的PRTV可以使用特征值计算,如下所示:

肘部规则
肘部规则或肘部法是一种启发式方法,用于根据 PCA 结果确定最佳主成分的数量。该方法背后的思想是将解释的变异绘制为分量数的函数,并选择曲线的弯头作为最佳主分量的数量。下面是此类散点图的示例,其中PRTV(Y轴)绘制在主分量的数量(X轴)上。弯头对应于 X 轴值 2,这表明最优主成分的数量为 2。
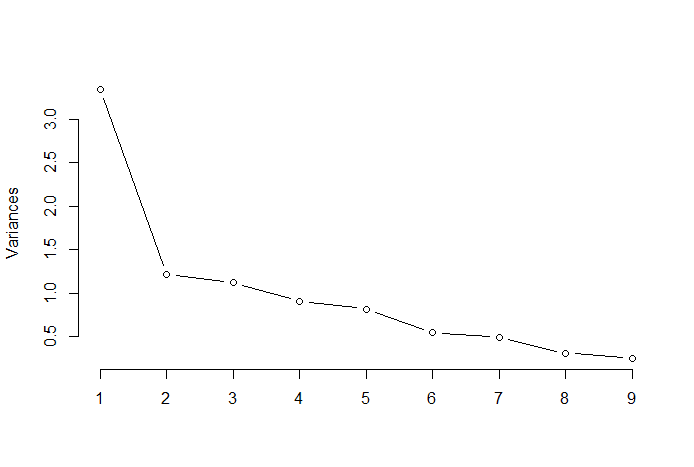
图片来源:多元统计 Github
因子分析
因子分析或 FA 是另一种降维统计方法。它是最常用的相互依存技术之一,当相关变量集显示出系统的相互依存关系并且目标是找出产生共同性的潜在因素时,就会使用这种技术。假设我们有一个带有 p 个变量的数据 X;X1, X2, ...., Xp. FA模型可以表示如下:

其中 X 是 p 个变量和 N 个观测值的 [p x N] 矩阵,μ是 [p x N] 总体均值矩阵,A 是 [p x k] 公因子载荷矩阵,F [k x N] 是公因子矩阵,u [pxN] 是特定因子矩阵。因此,换句话说,因子模型是一系列多元回归,根据不可观察的公共因子 fi 的值预测每个变量 Xi:

每个变量都有自己的 k 个公因子,这些因子通过单个观测值的因子加载矩阵与观测值相关,如下所示: 在因子分析中,计算因子以最大化组间方差,同时最小化组内变量e.它们是因子,因为它们对基础变量进行分组。与 PCA 不同,在 FA 中,数据需要归一化,因为 FA 假定数据集服从正态分布。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号