P4183 [USACO18JAN] Cow at Large P 题解

题意分析

我们首先想到，枚举贝茜在 $x$ 点，枚举度数大于 $2$ 的点为 $y$。设 $x$ 的度数为 $a$，$y$ 的度数为 $b$。

我们首先发现每个 $x$ 点都有一个初始的贡献为 $a$ 条通往叶子的路径。

如果点 $y$ 到最近的叶子节点的距离大于到 $x$ 的点的距离（农夫不能在 $y$ 点追上贝茜），则 $y$ 点可以贡献额外的 $b-2$ 条路径。（$y$ 的度数减去进入 $y$、离开 $y$ 的初始贡献消耗的度数）。

我们考虑先预处理出每个 $y$ 点到最近的叶子节点的距离为 $m{i}_y$。

void bfs(int x){
    queue<pair<int,int> >q;
    q.push(make_pair(x,0));
    bool v[70010]={};
    while(!q.empty()){
        int y=q.front().first,z=q.front().second;
        q.pop();
        for(int i=hea[y];i;i=nex[i]){
            int t=to[i];
            if(v[t]!=1){
                v[t]=1;
                if(siz[t]==1){
                    mi[x]=z+1;
                    return;
                }
                q.push(make_pair(t,z+1));
            }
        }
    }
}

然后再从 $x$ 点搜索出所有的 $y$ 点计算出合法贡献。注意不能加上自己。

void dfs(int x,int nu,int fa){
    if(siz[x]>2){
        if(nu<mi[x]&&nu!=0) ans+=siz[x]-2;
        tot++;
    }
    if(tot>=num) return ; 
    for(int i=hea[x];i;i=nex[i]){
        int t=to[i];
        if(t!=fa){
            dfs(t,nu+1,x);
        }
    }
}

我们发现这样会 TLE $5$ 个点。

我们考虑优化，我们发现枚举的 $x$ 点数量太多。我们可以枚举 $y$ 点反推 $x$ 点。

像这样：

void bf(int x){
    queue<pair<int,int> >q;
    q.push(make_pair(x,0));
    bool v[70010]={};
    while(!q.empty()){
        int y=q.front().first,z=q.front().second;
        q.pop();
        if(y!=x)
        an[y]+=siz[x]-2;
        if(z+1<mi[x])
        for(int i=hea[y];i;i=nex[i]){
            int t=to[i];
            if(v[t]!=1){
                v[t]=1;
                q.push(make_pair(t,z+1));
            }
        }
    }
}

证明一下复杂度：

我们考虑最坏复杂度，此时树为一棵满二叉树。

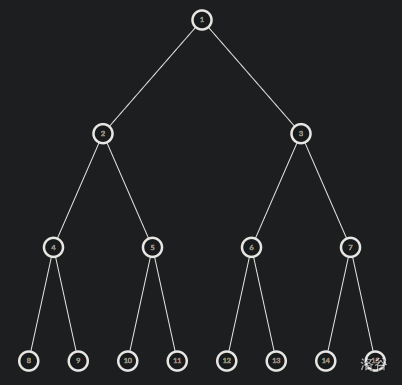
我们设树总共有 $m$ 层。

第 $1$ 层不会遍历。

第 $2$ 层有 $2^{2-1}$ 个数，每个数会遍历 $2^{m-1}-1+1$ 次。

有什么规律呢？

我们把向上的部分转移位置，例如 $2$ 号节点是这样的：

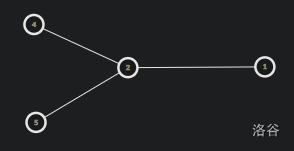
如果有更多节点，图就变成了这样。

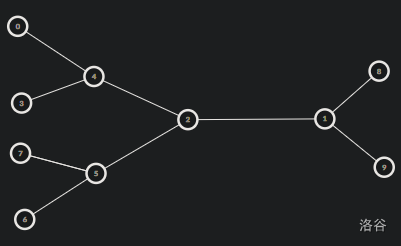
对于第 $i$ 层遍历了 $2^{i-1}\times (2^{m-i}-1+2^{m-i-1})$ 次。

化简一下并去掉常数就是 $2^{m-1}\times 2^{m-2}=3\times 2^{m-2}$ 次。

由于是一个满二叉树，节点数 $n=2^m-1$，$m\approx log(n)$。

所以复杂度就是 $m\times \frac{3}{4}\times 2^m\approx O(n\log n)$。

由于常数较小，故比点分治快。

code

#include<iostream>
#include<queue>
#include<cstdio>
#include<utility>
using namespace std;
int n,siz[70010],mi[70010],num,ans,ma;
int tot,hea[70010],nex[200010],to[200010],an[70010];
void add(int x,int y){
    to[++tot]=y;
    nex[tot]=hea[x];
    hea[x]=tot;
}
void bfs(int x){
    queue<pair<int,int> >q;
    q.push(make_pair(x,0));
    bool v[70010]={};
    while(!q.empty()){
        int y=q.front().first,z=q.front().second;
        q.pop();
        for(int i=hea[y];i;i=nex[i]){
            int t=to[i];
            if(v[t]!=1){
                v[t]=1;
                if(siz[t]==1){
                    mi[x]=z+1;
                    return;
                }
                q.push(make_pair(t,z+1));
            }
        }
    }
}
void bf(int x){
    queue<pair<int,int> >q;
    q.push(make_pair(x,0));
    bool v[70010]={};
    while(!q.empty()){
        int y=q.front().first,z=q.front().second;
        q.pop();
        if(y!=x)
        an[y]+=siz[x]-2;
        if(z+1<mi[x])
        for(int i=hea[y];i;i=nex[i]){
            int t=to[i];
            if(v[t]!=1){
                v[t]=1;
                q.push(make_pair(t,z+1));
            }
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
        siz[x]++;
        siz[y]++;
    }
    for(int i=1;i<=n;i++){
        if(siz[i]>2){
            bfs(i);
            num++;
            ma=max(ma,mi[i]);
        }
    }
    for(int i=1;i<=n;i++){
        if(siz[i]>2){
            bf(i);
        }
    }
    for(int i=1;i<=n;i++){
        if(siz[i]==1){
            printf("1\n");
        }
        else{
            ans=siz[i];
            tot=0;
            printf("%d\n",ans+an[i]);
        }
    }
    return 0;
}