剑指offer - 链表

1.从尾到头打印链表

问题描述：

输入一个链表，按链表从尾到头的顺序返回一个 ArrayList。

/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/
function printListFromTailToHead(head) {
  // write code here
  var result = [];
  while (head) {
    result.unshift(head.val);
    head = head.next;
  }
  return result;
}

2.链表中环的入口结点

问题描述：

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出 null。

方法一：

遍历这个链表，将结点存入数组中，给每次加入的结点做一个判断：是否这个结点已经保存在数组，如果保存过，说明这个结点就是环的入口节点

/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/

function EntryNodeOfLoop(pHead) {
  // write code here
  if (!pHead) return null;
  var arr = [];
  var node = pHead;
  while (node) {
    if (arr.includes(node)) {
      return node;
    }
    arr.push(node);
    node = node.next;
  }
  return null;
}

方法二：

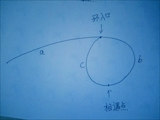
设置快慢指针，都从链表头出发，快指针每次走两步，慢指针一次走一步，假如有环，一定相遇于环中某点(结论 1)。接着让两个指针分别从相遇点和链表头出发，两者都改为每次走一步，最终相遇于环入口(结论 2)。以下是两个结论证明：
两个结论：

1. 设置快慢指针，假如有环，他们最后一定相遇。
2. 两个指针分别从链表头和相遇点继续出发，每次走一步，最后一定相遇与环入口。

证明结论 1:

设置快慢指针 fast 和 slow，fast 每次走两步，slow 每次走一步。假如有环，两者一定会相遇（因为 slow 一旦进环，可看作 fast 在后面追赶 slow 的过程，每次两者都接近一步，最后一定能追上）。

证明结论 2:

设：

• 链表头到环入口长度为--a
• 环入口到相遇点长度为--b
• 相遇点到环入口长度为--c

则：相遇时

快指针路程=a+(b+c)k+b ，k>=1 其中 b+c 为环的长度，k 为绕环的圈数（k>=1,即最少一圈，不能是 0 圈，不然和慢指针走的一样长，矛盾）。

慢指针路程=a+b

快指针走的路程是慢指针的两倍，所以：

（a+b）*2=a+(b+c)k+b

化简可得：

a=(k-1)(b+c)+c 这个式子的意思是： 链表头到环入口的距离=相遇点到环入口的距离+（k-1）圈环长度。其中 k>=1,所以 k-1>=0 圈。所以两个指针分别从链表头和相遇点出发，最后一定相遇于环入口。

/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/

function EntryNodeOfLoop(pHead) {
  // write code here
  if (pHead == null) {
    return null;
  }
  if (pHead.next == null) {
    return null;
  }
  var fast = pHead;
  var slow = pHead;
  while (slow != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    if (fast == slow) break;
  }

  var p1 = slow;
  var p2 = pHead;
  while (p1 != p2) {
    p1 = p1.next;
    p2 = p2.next;
  }
  return p1;
}

3.删除链表中重复的结点

问题描述：

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，链表 1->2->3->3->4->4->5 处理后为 1->2->5

解题思路：

借助一个辅助头节点，设置两个指针 pre 和 cur 分别指向上一个结点和当前结点，当 cur 的值和 cur.next 的值相等就让 cur 往前走，直到不相等的时候退出循环，这时候 cur 还是重复值，令 cur 再往前走一位，调整 pre 和 cur 再次进行判断。

举例：1->2->3->3->3->4->5 两个指针的走向如下

• -1(辅助头结点)->1->2->3->3->3->4->5
• -1(pre)->1(cur)->2->3->3->3->4->5
• -1->1(pre)->2(cur)->3->3->3->4->5
• -1->1->2(pre)->3(cur)->3->3->4->5
• -1->1->2(pre)->3->3(cur)->3->4->5
• -1->1->2(pre)->3->3->3(cur)->4->5
• -1->1->2(pre)->3->3->3->4(cur)->5
• -1->1->2(pre)->4(cur)->5
• -1->1->2->4(pre)->5(cur)

/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/

function deleteDuplication(pHead) {
  // write code here
  if (!pHead) return null;
  var head = new ListNode(-1); //辅助头节点
  head.next = pHead;
  var pre = head;
  var cur = head.next;
  while (cur !== null) {
    if (cur.next !== null && cur.next.val === cur.val) {
      while (cur.next !== null && cur.next.val === cur.val) {
        cur = cur.next;
      }
      cur = cur.next;
      pre.next = cur;
    } else {
      pre = cur;
      cur = cur.next;
    }
  }
  return head.next;
}