数据结构与算法之美【三】基础篇-链表
链表 Linked List 与LRU缓存策略
本文内容,单链表、双向链表与循环链表。单链表实现LRU的机制。回文单链表的判断。
链表
和数组不同,链表的内存空间不是连续的,因此相对数组的操作更加灵活,它通过“指针”将各个结点连接起来。链表的由结点连接而成,每个结点内存放了数据和指向下一个节点的指针。这里介绍三种链表:单链表、双向链表和循环链表。
单链表:是最简单的链表,其中有两个特殊的结点,第一个和最后一个。
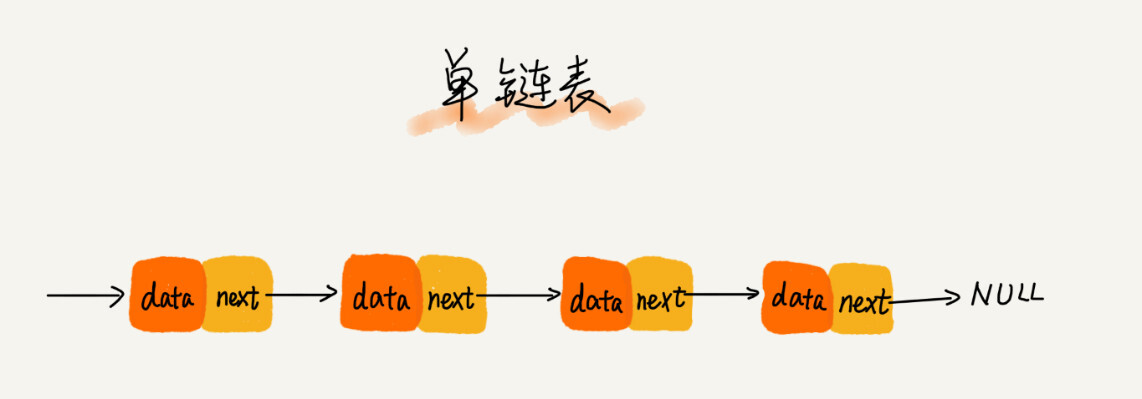
头结点记录链表的基地址,通过它可以遍历整个链表,尾结点指向NULL指针,标志着结束。
单链表插入和删除操作,复杂度都是O(1)。
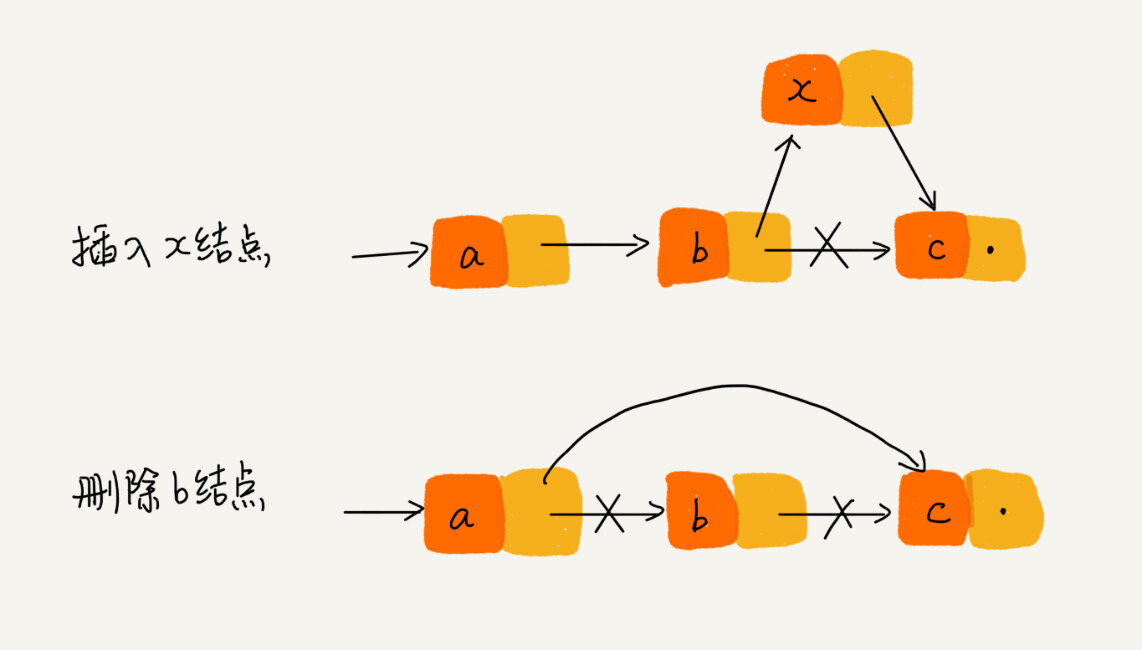
但是访问链表的某个结点,相对数组就比较麻烦,只能通过遍历的方式访问。
循环链表和双向链表。循环链表是一种特殊的单链表,不同之处在于尾结点的指针不是指向空地址,而是指向首指针。
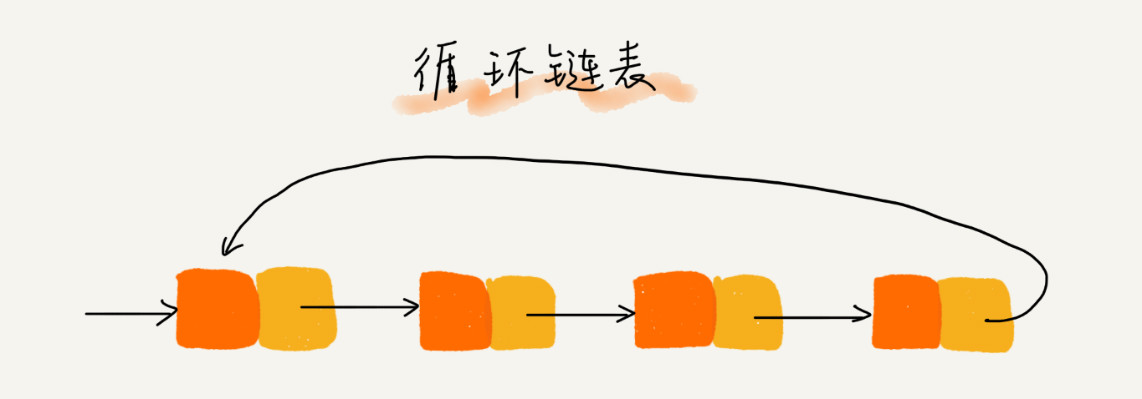
循环链表适合具有环形结构的数据,如约瑟环问题。
双向链表则不同,双向链表在单链表的基础上多了一个指向前结点的指针。
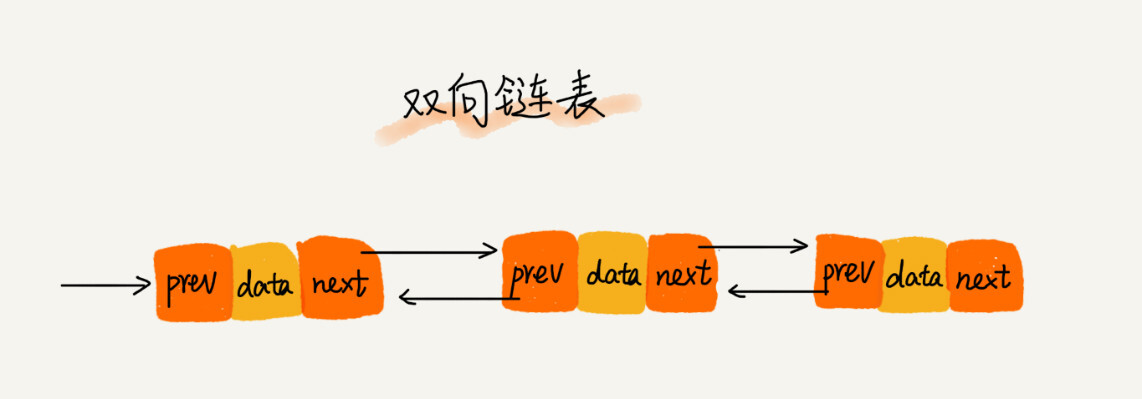
前面 单链表的插入和删除操作,分析复杂度是O(1)。但这是理论上的,实际并不准确。以删除操作为例,要么删除链表中值为某个给定值的结点,或者删除某个指针指向的结点。
对于删除某个指定值的结点,单 删除 操作的时间复杂度是O(1)。但是需要遍历单链表寻找到这个值所在的结点,这个过程是比较耗时的,总的时间复杂度是O(n)。
对于删除某个指针指向的结点q,我们还需要知道q的前驱结点才能执行操作,因为需要把 q的前驱结点 的指针 修改为 q的后继结点。从而达到删除目的。而单链表是无法直接知道前驱结点的,需要遍历,直到 p->next = q,才能找到前驱结点。
对于双向链表,如果是指针指向的某结点,它的删除操作是真正的O(1)复杂度,只需要将其前驱结点的指针修改即可。插入操作同理。
因此,双向链表的插入删除效率相对较高,但是空间内存消耗更大。
结合双向链表和循环链表的叫,双向循环链表。
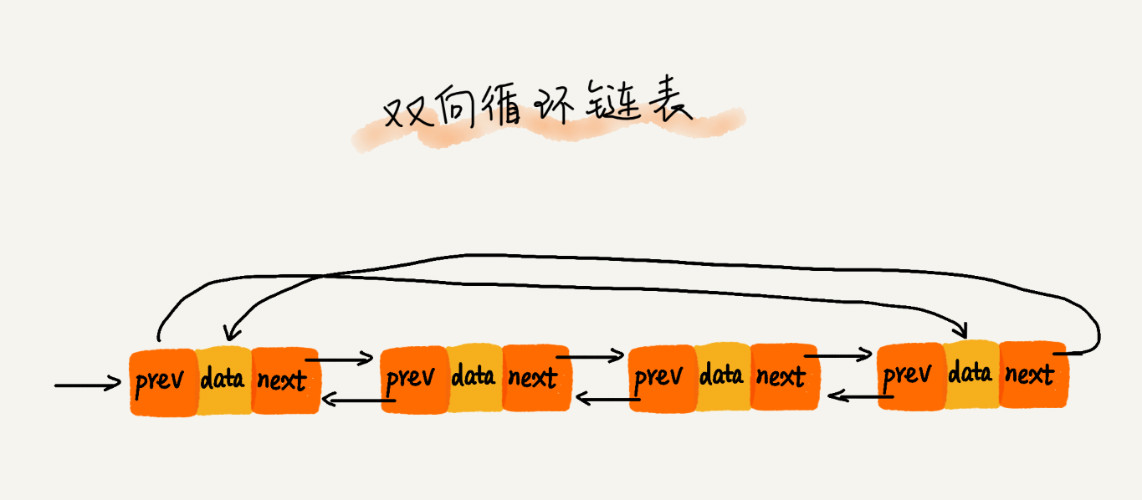
数组和链表的对比。
数组简单易用,在实现上使用的是连续的内存空间,可以借助 CPU 的缓存机制,预读数组中的数据,所以访问效率更高。而链表在内存中并不是连续存储,所以对 CPU 缓存不友好,没办法有效预读。
数组的缺点是大小固定,一经声明就要占用整块连续内存空间。如果声明的数组过大,系统可能没有足够的连续内存空间分配给它,导致“内存不足(out of memory)”。如果声明的数组过小,则可能出现不够用的情况。这时只能再申请一个更大的内存空间,把原数组拷贝进去,非常费时。链表本身没有大小的限制,天然地支持动态扩容,我觉得这也是它与数组最大的区别。
你可能会说,我们 Java 中的 ArrayList 容器,也可以支持动态扩容啊?我们上一节课讲过,当我们往支持动态扩容的数组中插入一个数据时,如果数组中没有空闲空间了,就会申请一个更大的空间,将数据拷贝过去,而数据拷贝的操作是非常耗时的。
我举一个稍微极端的例子。如果我们用 ArrayList 存储了了 1GB 大小的数据,这个时候已经没有空闲空间了,当我们再插入数据的时候,ArrayList 会申请一个 1.5GB 大小的存储空间,并且把原来那 1GB 的数据拷贝到新申请的空间上。听起来是不是就很耗时?
除此之外,如果你的代码对内存的使用非常苛刻,那数组就更适合你。因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针,所以内存消耗会翻倍。而且,对链表进行频繁的插入、删除操作,还会导致频繁的内存申请和释放,容易造成内存碎片,如果是 Java 语言,就有可能会导致频繁的 GC(Garbage Collection,垃圾回收)。
所以,在我们实际的开发中,针对不同类型的项目,要根据具体情况,权衡究竟是选择数组还是链表。
LRU缓存淘汰算法
这个问题是课程开篇提出的,如下。
缓存是一种提高数据读取性能的技术,在硬件设计、软件开发中都有着非常广泛的应用,比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。
缓存的大小有限,当缓存被用满时,哪些数据应该被清理出去,哪些数据应该被保留?这就需要缓存淘汰策略来决定。常见的策略有三种:先进先出策略 FIFO(First In,First Out)、最少使用策略 LFU(Least Frequently Used)、最近最少使用策略 LRU(Least Recently Used)。
可以使用单链表实现LRU缓存淘汰。方法如下:
维护一个单链表,越靠近尾部的结点是越早访问的,当有新的数据时,从表头开始遍历链表。如果链表中已经有了该数据,那么将其从原来的位置删除,再将其插入到链表的头部。如果链表中没有该数据,那么判断缓存容量是否已经满了,如果满了就需要删除尾部结点,然后在头部插入数据,容量还没有满的话就可以直接插入数据。
这种方法实现的LRU缓存,时间复杂度是O(n),不管多大,都需要遍历链表,寻找缓存位置。另外一种降低复杂度的方式是利用散列表记录每个缓存数据的位置,这样时间复杂度就降到了O(1)。
思考题 回文串
如何判断一个字符串是否是回文串,字符串使用单链表存储。
快慢指针法。回文字符串的特点是顺序和倒序一样,实际上就是分成两半,左半部分翻转后和右半部分一致即可。如一个单链表"a -> b -> c -> b -> a"。
我们可以使用两个指针来遍历链表,一个快指针和一个慢指针,快指针每次前进两步,而慢指针每次前进一步。
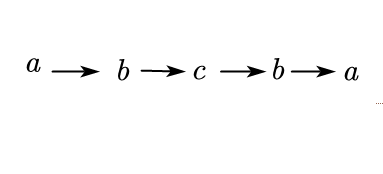
如上,开始时快指针p和慢指针q都指向a,第一次遍历后,p指向了c,而q指向了b,然后第二次遍历p指向了尾结点,而q刚好来到了中间结点(奇数的情况),如果结点个数是偶数,类似地,p指针最后指向的是NULL,而q指针指向中间第\(\frac n 2\)节点,结点个数位为\(n\)。可以看到,如果是奇数,那么按照快慢指针的遍历,当快指针结束,慢指针指向正中间,它的左边就刚好是一半结点,判断它与右边的另一半是否翻转后相同即可,如果是偶数,那么是p左边的部分,和p->next的后面部分,另外要判断p和p->next是否相同。
另外,翻转左边部分链表的操作在遍历的过程完成即可,当慢指针遍历一个节点后,将其倒向指向前一个节点,这样当p遍历完,左边也倒向了。然后判断倒向后的左边和右边是否相同即可,或者定了中点后,将中点后的数据进行倒向,然后判断其与前半部分是否相同。
python实现的代码如下。其中链表的定义是课程的代码链接https://github.com/wangzheng0822/algo 中的定义。
def is_palindrome(l):
l.print_all() # 单链表
slow = l._head
fast = l._head # 慢指针和快指针
position = 0 # 记录为证
while fast and fast._next: # 快指针还未遍历完
slow = slow._next # 慢指针每次走一步
fast = fast._next._next # 快指针每次走两步
position += 1 # 位置加1 如果是奇数,刚好在正中间、
# 倒置后半部分
pre = None # 用来存放 前 结点,中间结点指向的 前结点是 none
cur = slow # 当前节点
next_node = slow._next # 下一个节点
while cur._next : # 只要下一个节点不空
cur._next = pre # 将当前节点指向 前一个节点。 前一个节点pre的初始化是 None ,中间结点指向他
pre = cur # 然后记录当前这个节点,因为他是 下一个节点的 前驱结点
cur = next_node # 当前节点就前进一位 他是 下一个节点
next_node = cur._next # 然后再下一个
# 现在cur 是原先链表最后一个节点了,指向none,修改它指向前面的节点 cur._next = None
cur._next = pre
# 上述过程完成了后半段倒置。遍历cur即可
head = l._head
while cur._next : # 遍历cur
if head.data != cur.data :
return False
head = head._next
cur = cur.next
return cur.data == head.data # 显然如果是奇数,最后两头走到同一个地方,否则是中间相邻的两个数,
几个常见的链表问题,单链表反转,链表中环的检测,两个有序的链表合并,删除链表倒数第 n 个结点,求链表的中间结点。
单链表翻转
翻转问题在之前的回文串已经使用过,方法很简单,记录当前位置的下一个节点,修改当前指针指向上一个节点。
def reverse(link_list):
# 输入原链表 返回结点,作为倒序链表的头部节点即可
head = link_list._head # 头部节点
cur = head # 当前位置节点
pre = None
while cur._next:
# 遍历
next_node = cur._next # 记录下一个节点
cur._next = pre # 修改当前节点的指向
pre = cur
cur = next_node # cur前进一位
cur._next = pre # 原链表的最后一个节点
return cur
# 测试
from singly_linked_list import SinglyLinkedList
link_list = SinglyLinkedList()
string = "abcde"
for str in string:
# 依次将数据插入链表头 从而构造一个链表
#link_list.insert_to_head(str)
link_list.insert_value_to_head(str)
print("原始链表如下:\n")
link_list.print_all() # e->d->c->b->a
reverse_list = SinglyLinkedList() # 倒序链表
reverse_head = reverse(link_list) # 倒序链表的头部
reverse_list._head = reverse_head # 添加头部到链表
reverse_list.print_all() # a->b->c->d->e
环的检测
由于单链表的特殊性,只可能出现形如ABCDEFB这种环,而不会有ABCDEFBG这种环。即在链表的中间部分形成环(出入口各一个的环),因此可以通过快慢指针检测环,慢指针每次走一步,快指针每次走两步,如果有环,那么他们肯定会相遇。
def has_ring(link_list):
fast, slow = link_list._head, link_list._head
while fast and fast._next :
slow = slow._next
fast = fast._next._next
if slow == fast:
return True
return False
两个有序链表合并
两个有序链表合并,合并后依然保持有序,使用两个指针在链表上移动,每次移动对比即可。
def merge(l1,l2):
if l1._head and l2._head:
# 两个链表都有数据的话
p1, p2 = l1._head, l2._head # 两个指针指向头
head = Node(None) # 新链表的头结点 实际的节点头
cur = head # 一个记录当前位置的, 现在他指向这个None结点。在while中
# 第一次循环它就修改了head.next指向了两个链表的首元素较小的那个
while p1 and p2:
# 遍历两个指针
if p1.data <= p2.data:
# l1当前的结点值小,那么在新的链表节点加入l1
cur._next = p1
p1 = p1._next # p1加入新链表后,后移一位
else:
cur._next = p2
p2 = p2._next
cur = cur._next # cur后移一位
# while循环遍历后 可能会有某一个链表还剩一部分的情况,直接加入新链表即可
cur._next = p1 if p1 else p2
return head._next #head本身的数据是none,它的next才指向由l1 l2排序后的地方
return l1._head or l2._head # 如果有一个是空列表。直接返回不空的那个即可
删除倒数第n个结点
删除倒数的结点需要先找到结点的位置,倒数第n个位置的寻找有多种方法。
第一种,遍历整个链表,记录结点个数N,那么第\(N-(n-1)\)个结点就是要删除的倒数第n个位置,(头结点是第1结点),然后再遍历\(N-n+1\)个结点即可。
第二种,两个指针遍历链表,第一个指针提前走,走\(n-1\)步,然后两个指针开始同时走,直到第一个指针走完链表。那么此时,第一个指针比第二个指针多走了\(N-n+1\)步,而此时的第一个指针在尾结点,它向前倒退\(n\)个位置就是现在第二个指针的位置。
上述两种方法的原理是一样的。另外排除特殊情况,节点总个数不足\(n\)或者刚好\(n\)的情况。
def remove_nth(L1: SinglyLinkedList, n:int):
fast = L1._head
slow = L1._head # 两个指针的方式
count = 0
while fast and count < n :
# 让快指针先走 n-1 步
fast = fast._next
count += 1
if not fast and count < n : # 总节点数小于n
# 但fast是空的了
return head # 直接返回头部
if not fast and count == n:
# 刚好走完 且 fast空了 总节点数恰好是 n
return head._next
while fast._next :
# 继续遍历 同时行走
fast, slow = fast._next, slow._next
slow._next = slow._next._next # 修改指向下下个即可
return L1._head
求链表的中间结点
两种方法,第一种遍历全部,得到链表的长度\(n\),然后遍历到第\(\frac n 2\)处即可。第二种,仍然是快慢指针,一个走两步,一个走一步,显然当快指针走完,慢指针刚好在中间。
def find_middle_node(head):
slow, fast = head, head
fast = fast._next if fast else None
while fast and fast._next:
slow, fast = slow._next, fast._next._next
return slow


