数据结构与算法之美【一】-入门篇四讲

数据结构与算法之美

本文为极客时间王铮的课程专栏总结笔记。目录大部分按照课程的安排，部分有所出入。

入门篇

路线与课程内容

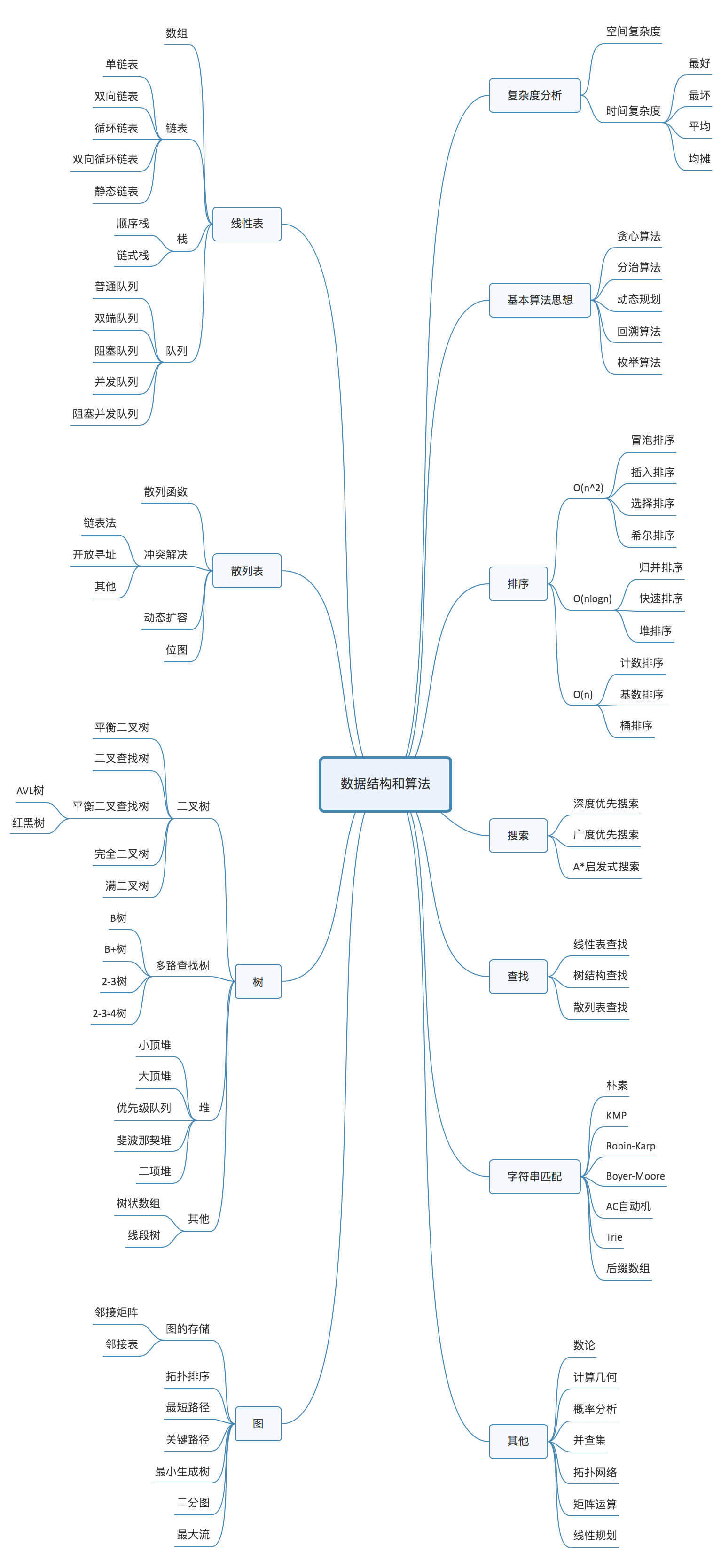
课程的概览：涉及到的数据结构包括： 数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、树 ，算法则包括 递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算
法、动态规划、字符串匹配算法。

题外话：一个可以将算法可视化的辅助网站 https://www.cs.usfca.edu/~galles/visualization/

时间复杂度分析

大O复杂度表示法 ： \(T(n)=O(f(n))\) ，其中T(n) 表示代码执行的时间；n 表示数据规模的大小；f(n) 表示每行代码执行的次数总和。公式中的 O，表示代码的执行时间 T(n) 与 f(n) 表达式成正比。大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

怎么分析一段代码的时间复杂度呢？

1. 只关注循环次数最多的一段代码，大O复杂度表示方法只是一种变化趋势，因此常忽略常量、低阶和系数，记录最大的量级即可。

   int cal(int n ){
       int sum = 0;   // 常量的时间不计
       int i = 1;  
       for(; i<=n ; ++i){
           sum += i;  // 运行n次循环 因此这段代码的时间复杂度是O(n)
       }
       return sum;
   }
   

2. 加法法则： 总复杂度等于量级最大的那段代码的复杂度

   int cal(int n) {
      int sum_1 = 0;
      int p = 1;
      for (; p < 100; ++p) {   //这一段是常量级别 100 ，不管这个数多大，只要它是常数，都认为是常量级别
        sum_1 = sum_1 + p; // 在n无限大时都可以忽略不计
      }
    
      int sum_2 = 0;
      int q = 1;
      for (; q < n; ++q) {  // 这一段是 n 
        sum_2 = sum_2 + q;
      }
    
      int sum_3 = 0;
      int i = 1;
      int j = 1;
      for (; i <= n; ++i) {  // 这一段是 n^2   最大，因此整段代码的时间复杂度是 O(n) = n^2
        j = 1; 
        for (; j <= n; ++j) {
          sum_3 = sum_3 +  i * j;
        }
      }
    
      return sum_1 + sum_2 + sum_3;
    }
   

3. 乘法法则：嵌套代码的复杂度等于嵌套内外复杂度的乘积

   int cal(int n) {
      int ret = 0; 
      int i = 1;
      for (; i < n; ++i) {
        ret = ret + f(i);  // 如果考虑f(i)的复杂度是常量，显然这里的是 n
      } 
    } 
    
    int f(int n) {  // 但是f函数的复杂度也是n 因此cal操作的复杂度是n*n = n^2
     int sum = 0;
     int i = 1;
     for (; i < n; ++i) {
       sum = sum + i;
     } 
     return sum;
    }
   

常见的时间复杂度

可以粗略分为两类，多项式和非多项式复杂度，非多项式的是\(O(log ~n)\)和\(O(n!)\)。

\(O(1)\) : 这类复杂度的代码，执行时间不随n的变化而变化，就可以认为是1。

\(O(log ~n )~、O(n~log ~n))\) : 前者的一个典型例子是

i = 1;
while (i <= n)
    i = i*2 ; 
// 事实上，这段代码的执行次数是 log_2(n) ,当执行x次结束循环，此时的i = 2^x >= n,因此 x >= log(n)

\(O(m+n)、O(m*n)\): 这种代码的复杂度有两个数据规模决定，即程序中有两部分未知的，因此不能简单省略其中一个。

空间复杂度分析

大O表示法针对的算法执行时间与数据规模的增长关系，空间复杂度即渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。常见的空间复杂度是\(O(1)、O(n)、O(n^2)\)，其他的对数级别等不常用。空间复杂度的分析，直接代码中申请的数据存储空间即可。

复杂度分析进阶

以在数组中寻找某个元素的位置为例，找到则返回其索引位置，反之则返回-1。代码如下。

int find(int[] array, int n,int x )
{
    int i = 0;
    int pos = -1;
    for (;i< n ; i++)
    {
        if (array[i] == x) 
        {
            pos=i;break;
    }
    return pos;
}

显然，如果不加break，这个函数的时间复杂度明显是\(O(n)\)，但是当在实际分析时，要加上break，因为程序可能提前终止，对具体的数据而言，上述代码(加了break的) 的复杂度就分情况了，最理想的情况，第一个元素就是要查找的值，复杂度变成\(O(1)\)，最不理想的情况，查找的数字不在数组内，则要把整个数组遍历一次，复杂度是\(O(n)\)，前者称为最好情况时间复杂度，后者称为最坏情况时间复杂度。

无论是最好还是最坏，它们都是在极端情况下的分析，而一般的，我们会考虑平均情况下的复杂度分析，称为平均情况时间复杂度。

以上述查找元素为例，返回的结果有\(n+1\)种情况：在索引位置0、1、、、、n-1和不在数组内的-1。每一种情况要遍历的元素个数是1、2、….、n和n(不在数组内)。然后计算每种情况的遍历元素之和，除以情况总数，就可以认为是平均情况，如下所示。

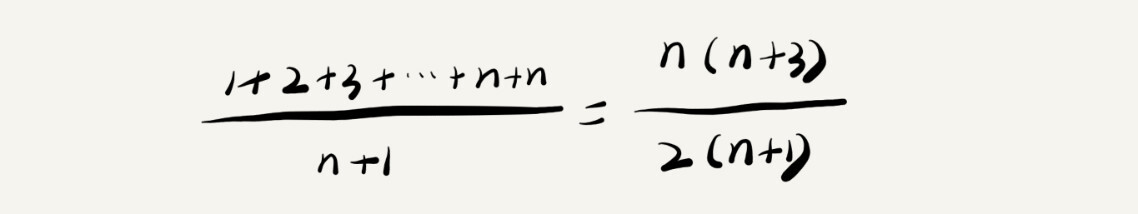
省略掉低阶、系数、常量，计算出的平均时间复杂度是\(O(n)\)。

但是，再仔细一想，返回的n+1种结果出现的概率并不是等同的，上面的分析是默认了各个情况出现的概率一致。事实上，更能被接受的是，要查找的元素出现和不在数组中的概率是一样的，为1/2，而如果元素出现在数组中，那么出现在各个位置的概率也是一样的，即1/n，根据概率的计算规则，元素出现在这n个位置中的任意一个的概率是1/2 * 1/n = 1/(2n)。

那么，考虑了概率的复杂度计算应该是

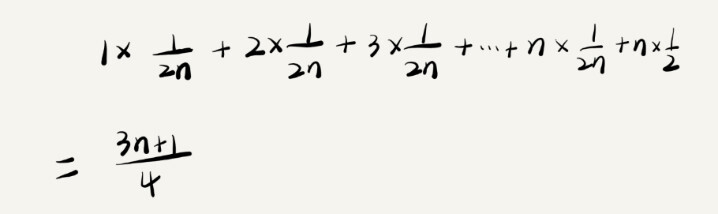
这个值实际上是期望，尽管用大O法表示，上面两种分析的结果是一样的。

平均情况时间复杂度仅在很少情况下与最好和最坏情况进行区分，即当这几个情况下，代码的复杂度有量级时，才会进行区分。另外一个概念是均摊时间复杂度。

均摊时间复杂度是一种特殊的平均复杂度。使用的场景更加有限，通常是在有连续操作的情况下分析。比如在每一次\(O(n)\)操作后，都跟着n-1次的\(O(1)\)操作，这样，我们可以把两个连续操作放在一起分析，将时间复杂度高的部分，平摊到比较低的操作上。课程中例子如下，在数组中插入数据。

int[] array = new int[n];
int count = 0;
 
void insert(int val) {
    if (count == array.length) {  // 如果数组已经满了，那么把数组情况，求和，将和作为数组第一个数
       int sum = 0;               // 然后将要插入的val放在第二个位置
       for (int i = 0; i < array.length; ++i) {
          sum = sum + array[i];
       }
       array[0] = sum;
       count = 1;
    }
 
    array[count] = val;  // 如果要插入的位置没有越界，直接放即可
    ++count;
 }

这个示例用于分析均摊时间复杂度，是\(O(1)\)。