MCNN: 多列卷积神经网络的单图像人群计数
MCNN网络
论文PDF
作者源码,使用matlab处理数据集,torch实现网络。
MCNN是上海科技大学在CVPR 2016上的一篇论文,使用3列卷积网络进行人群密度估计。
摘要
本文旨在提出一种弄可以从具有任意人群密度和角度的的单张图像准确估计人群数量的方法。为了实现这个目的,我们提出一种简单但是很有效的多列卷积神经网络(MCNN),将图像映射到它的人群密度图。MCNN允许输入图像是任意大小和分辨率。通过利用不同大小的滤波器(核)有不同大小的感受野,每一列的CNN学习到的特征由于透视效果或者图像分辨率而适应对人头大小的变化(这句大概就这意思)。此外,真实密度图的准确计算依赖于几何自适应核(geometry-adaptive kernels ),它不需要知道输入图像的透视图(???)。由于现有的人群计数数据集不足以涵盖我们工作中考虑的所有具有挑战性的情况,因此我们收集并标记了一个大型的新数据集,其中包括1198幅图像,其中包含约330,000个头。在这个具有挑战性的新数据集以及所有现有数据集上,我们进行了广泛的实验,以验证所提出的模型和方法的有效性。特别是,通过提出的简单MCNN模型,我们的方法优于所有现有方法。此外,实验表明,一旦在一个数据集上进行训练,我们的模型就可以轻松转移到新的数据集上。
论文解读
该论文是在CVPR 2012的《 Multi-column deep neural networks for image classification》基础上提出的。MCNN的输出是人群密度图,它的积分值就是整张图像的人数估计,网络包含三列CNN,每一列的核大小等不同。
论文的三个贡献点:1. 使用多列结构,对应于大中小三种不同感受野大小的核,每列的特征可以适应人/头的较大差异变化。2. 使用1x1的卷积替换全连接层,因此,输入图像可以是任意大小以避免失真。 3. 收集图像制作了一个新的人群计数数据集。
通过CNN进行图像中的人数估计有两种思路:1. 输入图像输出估计的人头数目。2.输出人群密度图,如每平米多少人,然后通过积分计算人数。MCNN使用的是第二种。
由于需要对CNN进行训练以从输入图像中估计人群密度图,因此训练数据中给出的密度质量在很大程度上决定了方法的性能。我们首先描述如何将带有标签人头的图像转换为人群密度图。
在像素点\(x_i\)处如果有人头,我们将其表示为函数\(\delta(x-x_i)\),即在\(x=x_i\)处为1,其他地方全为0的函数。那么,一张图有\(N\)个人头的话,可以描述为函数\(H(x) = \sum_{i=1}^N \delta(x-x_i)\),为了将它转为一个连续密度函数,使用高斯核[1] \(G_{\sigma}\),密度可以描述为\(F(x)=H(x)*G_{\sigma}(x)\),但是这种密度函数假设了\(x_i\)是图像平面的独立样本,而实际上每个\(x_i\)都是场景中人去密度的样本(意思应该是,密度函数的假设是人头只占了一个像素点,是单独的独立样本,但是实际上,图像上每个点都是密度图的样本,由于透视畸变,与不同像本关联的像素点在场景中对应于不同大小的区域)。
In fact, each $x_i $ is a sample of the crowd density on the ground in the 3D scene and due to the perspective distortion, and the pixels associated with different samples \(x_i\) correspond to areas of different sizes in the scene.
我们假设每个人的头部周围比较均匀,头部和它在图像中的\(k\) 个邻域的平均距离给出几何变形的合理估计,因此根据图像中每个人的头部大小确定传播参数\(\sigma\)。我们发现人头大小通常与拥挤场景中两个相邻人的中心之间的距离有关,作为一种折中,对于那些拥挤场景的密度图,我们建议根据每个人与邻域的平均距离来自适应地确定每个人的传播参数
对于图像中给定的每个头部\(x_i\),我们定义该像素点到它的\(k\)个最近邻域的距离为\(\{d^i_1,d^i_2,..,d^i_m\}\),那么平均距离则为\({\overline {d^i}}= \frac 1 m \sum_{j=1}^m d^i_j\),最终定义的密度函数为
我们将标签H与密度核进行卷积,密度核适应每个数据点周围的局部几何体,称为几何适应核。实验发现系数\(\beta=0.3\)表现最好。
通过图片和标注的头部坐标生成密度图的Python测试代码如下,根据原作者提供的matlab版本代码修改而来。
import scipy.io as io # 读取mat文件的坐标
import cv2 # 读取图像和在高斯核计算时使用
import numpy as np
from matplotlib import pyplot as plt # 显示
def fspecial(ksize_x=5, ksize_y = 5, sigma=4):
# 返回大小为(ksize,ksize)的二维高斯滤波器核矩阵
# 完全等价于matlab中的fspecial('Gaussian',[ksize, ksize],sigma);
kx = cv2.getGaussianKernel(ksize_x, sigma)
ky = cv2.getGaussianKernel(ksize_y, sigma)
return np.multiply(kx,np.transpose(ky))
pixes = io.loadmat('../GT_IMG_1.mat') # 读取标签,格式是dict
counts = pixes['image_info'][0][0][0][0][1][0][0] # 标签总人数
xy = pixes['image_info'][0][0][0][0][0] # (counts,2)的数组
img = cv2.imread('../IMG_1.jpg') # 原图
h, w = img.shape[0:2]
labels = np.zeros(shape=(h,w)) # 密度图 初始化全0
for loc in xy: # 遍历每个头部坐标
f_size = 15 # 核大小,也是要考虑的邻域大小
sgma = 4.0
H = fspecial(f_size, f_size , sigma) # 返回一个(15,15)的高斯核矩阵
x = min(abs(int(loc[0])),int(w)) # 头部坐标
y = min(abs(int(loc[1])),int(h)) # 防止越界
# 邻域的对角 考虑选择 (x1,y1) 到 (x2,y2) 区域
x1 = x - f_sz/2 ; y1 = y - f_sz/2
x2 = x + f_sz/2 ; y2 = y + f_sz/2
dfx1 = 0; dfy1 = 0; dfx2 = 0; dfy2 = 0 # 偏移
change_H = False
if x1 < 0 :
# 左上角在图像外了
dfx1 = abs(x1) # 偏移量就是它的绝对值
x1 = 0 # 左上角直接置零,源码中是1,因为matlab矩阵索引从0开始
change_H = True
if y1 < 0:
dfy1 = abs(y1)
y1 = 0
change_H = True
if x2 > w:
dfx2 = x2 - w
x2 =w-1 # 右下角超出,那么直接是最后一行/列,索引值是h-1和w-1
change_H =True
if y2 > h:
dfy2 = y2 -h
y2 = h-1
change_H =True
x1h = 1+dfx1
y1h = 1 + dfy1
x2h = f_size - dfx2 # x2h-x1h +1 = f_size - dfx2 - dfx1 其中dfx2+dfx1
y2h = f_size - dfy2 # y2h-y1h +1 = f_size - dfy2 -1 - dfy1 +1 = f_size - dfy2 - dfy1
if change_H:
H = fspecial(int(y2h-y1h+1), int(x2h-x1h+1),sigma)
labels[int(y1):int(y2), int(x1):int(x2)] = labels[int(y1):int(y2), int(x1):int(x2)] + H
plt.imshow(labels)
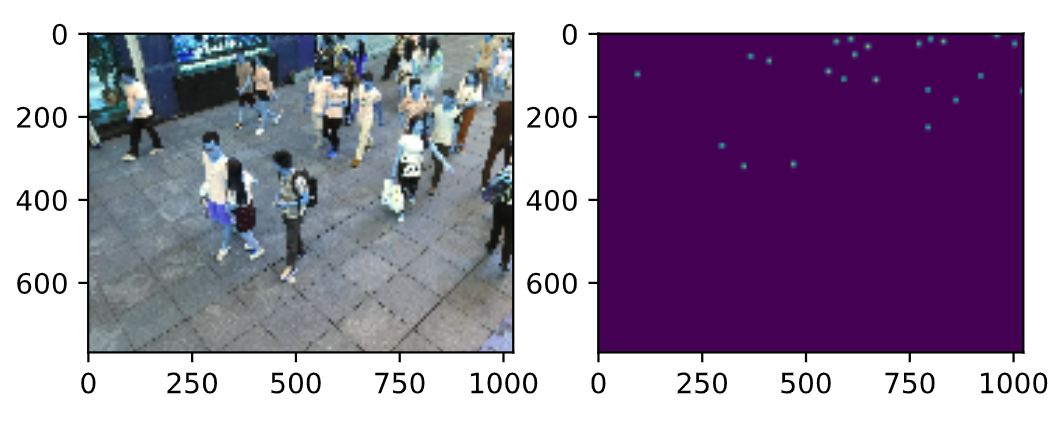
生成的ground_truth密度图如下。
MCNN的结构
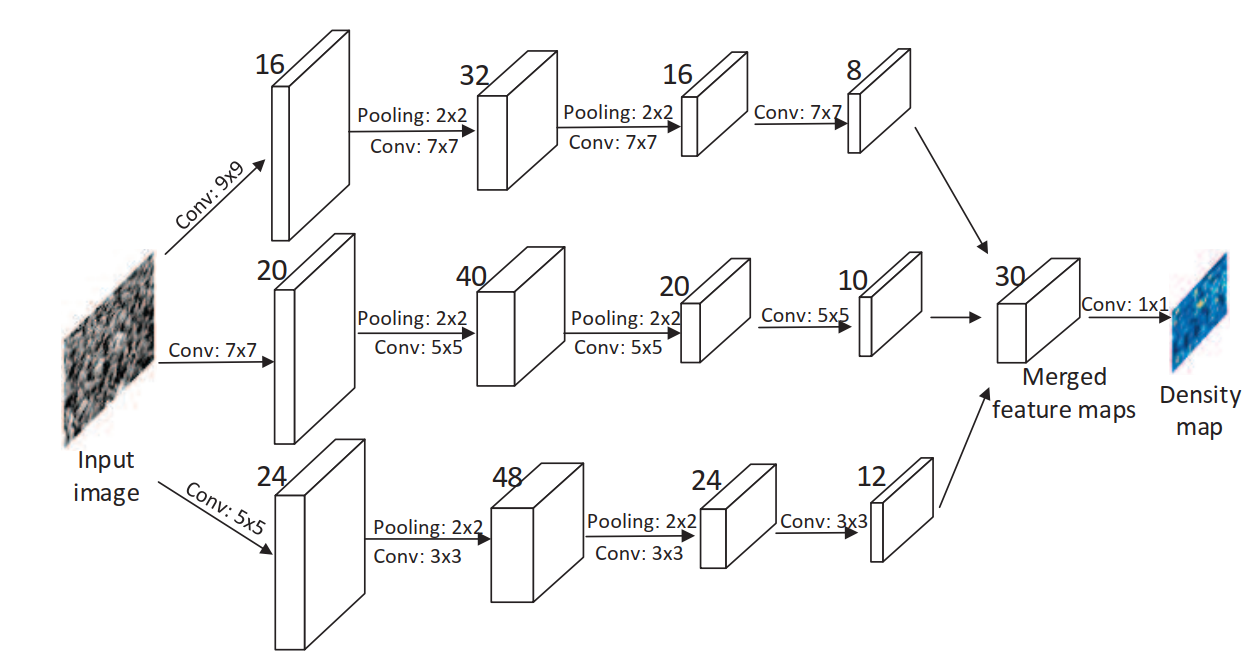
MCNN受多列DNN的启发,用三列并行的感受野大小不一的卷积网络构成,所有的列都使用了类似的结构(conv-pool-conv-pool),只是在数量和大小上有所区别。较大尺寸的卷积核采用较少的数量,堆叠所有的输出,然后将其映射到密度图,映射的方法采用了1x1卷积,然后使用欧式距离衡量预测密度图和gt的差异。损失函数定义为
其中\(\Theta\)是要学习的参数,\(N\)是图像数目,\(X_i\)是输入图像,\(F_i\)是真实的密度图,\(F(X_i;\Theta)\)表示预估的\(X_i\)的密度图,
注意 : 由于采用了两次池化,每次都是2x2,因此每张图像的空间分辨率后悔降低\(\frac 1 4\),因此,在训练阶段,生成密度图之前,我们要对每个样本图像进行1/4的降采样,另外与MDNN不同的是,在最后堆叠每一列网络的输出时,MDNN采用的是直接平均,而MCNN使用的是1x1卷积。
另外,受RBM的启发,我们直接将第四列卷积的输出映射到特征图,分别进行训练,然后使用这些预训练的CNN参数初始化整个MCNN,并进行微调。
torch实现
数据准备
上海科大数据集有两个part,A的人群比较密集,B则比较稀疏,标签格式是mat文件。对mat的处理在之前已经说明,通过它生成每张图的gt密度图。论文提供的matlab代码,将每张图生成密度图后,保存为csv文件,然后在训练时读取csv文件。这里我们直接使用密度图,不保存。
另外,论文中提到数据增强时,将图像中裁剪9个小块,每个小块是原图像的 1/4 大小。源码中也使用了这个,从图上抠出9个小块。这里我没有考虑,直接将整张图送入训练的。
import cv2
import scipy.io as sio
from torch.utils.data import DataLoader,Dataset
from torchvision import transforms
import os
import numpy as np
import torch
unloader = transforms.ToPILImage()
class myDatasets(Dataset):
def __init__(self,img_path, ann_path, down_sample=False):
# 图像路径文件夹 和 标签文件 文件夹 采用绝对路径
self.pre_img_path = img_path # 文件夹路径
self.pre_ann_path = ann_path
# 图像的文件名是 IMG_15.jpg 则 标签是 GT_IMG_15.mat
# 因此不需要listdir标签路径
self.img_names = os.listdir(img_path)
self.down = down_sample
def __getitem__(self, index):
# 该函数用于返回每一个sample
img_name = self.img_names[index] # index对应的图片名
mat_name = 'GT_' + img_name.replace('jpg','mat')
img = cv2.imread(self.pre_img_path + img_name,0)
anno = sio.loadmat(self.pre_ann_path + mat_name)
xy = anno['image_info'][0][0][0][0][0] # N,2的坐标数组
density_map = self.get_density(img, xy) # 密度图
img = img.astype(np.float32)
density_map = density_map.astype(np.float32)
h = img.shape[0]
w = img.shape[1]
ht1 = h //4 * 4
wd1 = w //4 * 4
img = cv2.resize(img, (wd1, ht1))
if self.down :
wd1 = wd1 //4
ht1 = ht1 //4
density_map = cv2.resize(density_map, (wd1, ht1))
density_map = density_map * ( (w*h) /( wd1 * ht1) ) # 放大16倍多
else:
density_map = cv2.resize(density_map, (wd1, ht1))
density_map = density_map * ( (w*h) /( wd1 * ht1) )
img = torch.from_numpy(img.reshape(1,img.shape[0], img.shape[1]))
density_map = torch.from_numpy(density_map.reshape(1,density_map.shape[0],density_map.shape[1]))
return img, density_map
def __len__(self):
return len(self.img_names)
def get_density(self,img, points):
h, w = img.shape[0], img.shape[1]
# 密度图 初始化全0
labels = np.zeros(shape=(h,w))
for loc in points:
f_sz = 17 # 滤波器尺寸 预设为15 也是邻域的尺寸
sigma = 4.0 # sigma参数
H = fspecial(f_sz, f_sz , sigma) # 高斯核矩阵
x = min(max(0,abs(int(loc[0]))),int(w)) # 头部坐标
y = min(max(0,abs(int(loc[1]))),int(h))
if x > w or y > h:
continue
x1 = x - f_sz/2 ; y1 = y - f_sz/2
x2 = x + f_sz/2 ; y2 = y + f_sz/2
dfx1 = 0; dfy1 = 0; dfx2 = 0; dfy2 = 0
change_H = False
if x1 < 0:
dfx1 = abs(x1);x1 = 0 ;change_H = True
if y1 < 0:
dfy1 = abs(y1); y1 = 0 ; change_H = True
if x2 > w:
dfx2 = x2-w ; x2 =w-1 ; change_H =True
if y2 > h:
dfy2 = y2 -h ; y2 = h-1 ; change_H =True
x1h = 1 + dfx1 ; y1h = 1 + dfy1
x2h = f_sz - dfx2 ; y2h = f_sz - dfy2
if change_H :
H = fspecial(int(y2h-y1h+1), int(x2h-x1h+1),sigma)
labels[int(y1):int(y2), int(x1):int(x2)] = labels[int(y1):int(y2), int(x1):int(x2)] + H
return labels
def fspecial(self,ksize_x=5, ksize_y = 5, sigma=4):
kx = cv2.getGaussianKernel(ksize_x, sigma)
ky = cv2.getGaussianKernel(ksize_y, sigma)
return np.multiply(kx,np.transpose(ky))
path1 = 'D://Datasets//part_B_final//train_data//images//'
path2 = 'D://Datasets//part_B_final//train_data//ground_truth//'
datasets = myDatasets(path1, path2)
train_loader = DataLoader(datasets, batch_size=1)
'''
x1 = None ; y1 = None
for x, y in train_loader:
x1 = x
y1 = y
break
unloader(x1.squeeze(0).squeeze(0))
unloader(y1.squeeze(0).squeeze(0)) # 可以简单测试查看数据
'''
模型搭建
MCNN一共有三个分支,每个分支都由卷积-池化-激活的小模块构成。最后的输出通道合并,通过1x1卷积映射到密度图。
import torch
import torch.nn as nn
class Conv2d(nn.Module):
# 定义了卷积 - 池化 -激活 的小模块
def __init__(self, in_channels, out_channels, kernel_size, stride=1, relu=True, same_padding=False, bn=False):
super(Conv2d, self).__init__()
padding = int((kernel_size - 1) / 2) if same_padding else 0
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding=padding)
self.bn = nn.BatchNorm2d(out_channels, eps=0.001, momentum=0, affine=True) if bn else None
self.relu = nn.ReLU(inplace=True) if relu else None
def forward(self, x):
x = self.conv(x)
if self.bn is not None:
x = self.bn(x)
if self.relu is not None:
x = self.relu(x)
return x
class MCNN(nn.Module):
# MCNN模块
def __init__(self, bn=False):
super(MCNN, self).__init__()
# 分支1 输出有8个通道
self.branch1 = nn.Sequential(Conv2d( 1, 16, 9, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(16, 32, 7, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(32, 16, 7, same_padding=True, bn=bn),
Conv2d(16, 8, 7, same_padding=True, bn=bn))
self.branch2 = nn.Sequential(Conv2d( 1, 20, 7, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(20, 40, 5, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(40, 20, 5, same_padding=True, bn=bn),
Conv2d(20, 10, 5, same_padding=True, bn=bn))
self.branch3 = nn.Sequential(Conv2d( 1, 24, 5, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(24, 48, 3, same_padding=True, bn=bn),
nn.MaxPool2d(2),
Conv2d(48, 24, 3, same_padding=True, bn=bn),
Conv2d(24, 12, 3, same_padding=True, bn=bn))
self.fuse = nn.Sequential(Conv2d( 30, 1, 1, same_padding=True, bn=bn))
def forward(self, im_data):
x1 = self.branch1(im_data)
x2 = self.branch2(im_data)
x3 = self.branch3(im_data)
x = torch.cat((x1,x2,x3),1) # 三个分支的输出合并
x = self.fuse(x) # 1x1 卷积 映射到 密度图
return x
训练
训练部分可以参考作者源码,修改数据的读取部分即可。


