极坐标系
元素:
· 极点:O
· 极轴:/vec OL
· 极径:r
· 极角: 注意是逆时针
注意是逆时针
· 极坐标: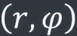
极坐标系与直角坐标系的转化:
r=dist(o,c)
/fi = tan(y,x);
极角排序
半平面内的极角排序(排序范围严格小于180°)
使用to-left测试(叉积比较),值越大的越在上方(对于右半平面来言)
必须严格小于!!因为极角大于等于180的时候to-left检测正好相反
全平面内的极角排序
法一:使用atan2(y,x)函数
不用tan(y,x)(因为会出现inf之类的情况)
先将所有点的极角算出来,然后按极角的值进行排序
注意边界点的值:
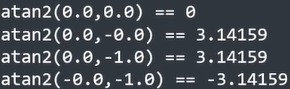
存在精度问题
法二:叉积比较
先划分上下平面,平面内进行叉积比较
注意:x轴正负半轴的点不能划分到同一平面内
下半平面 < 原点 < x正半轴 < 上半平面 < x负半轴
常数略大,但是基本无精度误差(因为基于整数域)
应用:
- 求凸包
- 半平面交
题目类型:
- 直线的旋转
- 平面整体旋转
- 利用极角序计数
题目技巧:
- 当过两个端点的时候可以固定一个端点然后极角排序,维护一个那些东西在区间内
- 巧妙利用对称(可以有效的降低常数)
code:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+10;
#define int long long
#define endl "\n"
struct Point{
int x,y;
void input(){cin>>x>>y;};
void output(){cout<<x<<' '<<y<<endl;};
};
int to_left(Point b,Point c){
Point a={0,0};
Point X={b.x-a.x,b.y-a.y},Y={c.x-a.x,c.y-a.y};
int ans=X.x*Y.y-X.y*Y.x;//差积
if(ans==0)return 0;
else if(ans>0)return 1;//c比b高
else return -1;
}
bool cmp(Point a,Point b){
int res=to_left(a,b);
if(res==0)return a.y<b.y;
return res>0;
}
void sol(){
int n;
cin>>n;
vector<Point>v[5];//分别为 负半平面 x正半轴 原点 正半平面 x负半轴
Point p;
for(int i=1;i<=n;i++){
p.input();
if(p.x==0 && p.y==0)v[2].push_back(p);
else if(p.y==0){
if(p.x>0)v[1].push_back(p);
else v[4].push_back(p);
}
else if(p.y<0)v[0].push_back(p);
else v[3].push_back(p);
}
for(int i=0;i<=4;i++){
sort(v[i].begin(),v[i].end(),cmp);
for(auto j:v[i]){
j.output();
}
}
}
signed main(){
// ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
sol();
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话