元素的表示
点
1. 复数类
· complex<int/duble>
· 特点:慢,自带各种运算,不怎么用
2. pair
· 自带排序
· 自由度不高
· 基本不在几何题目中使用
3.结构体
(推荐,常用)
自由度高,成员函数,重载运算符
struct Point{
double x,y;
};
向量
(直接用Point)
向量点积与几何意义及应用
\vec{a} \bullet \vec{b} =

warning:投影是有向的
向量叉积
值的大小等于以a和b为平行四边形两边的一个平行四边形的面积
利用叉积可以求角度的正弦值
两个向量的叉积还是向量(垂直于这两个向量所构成平面的一个向量)
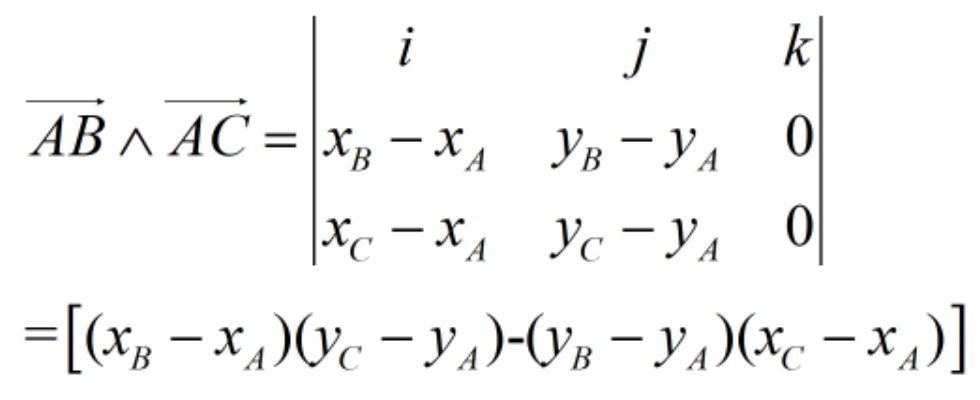
2024-04-18 22:11:00 星期四

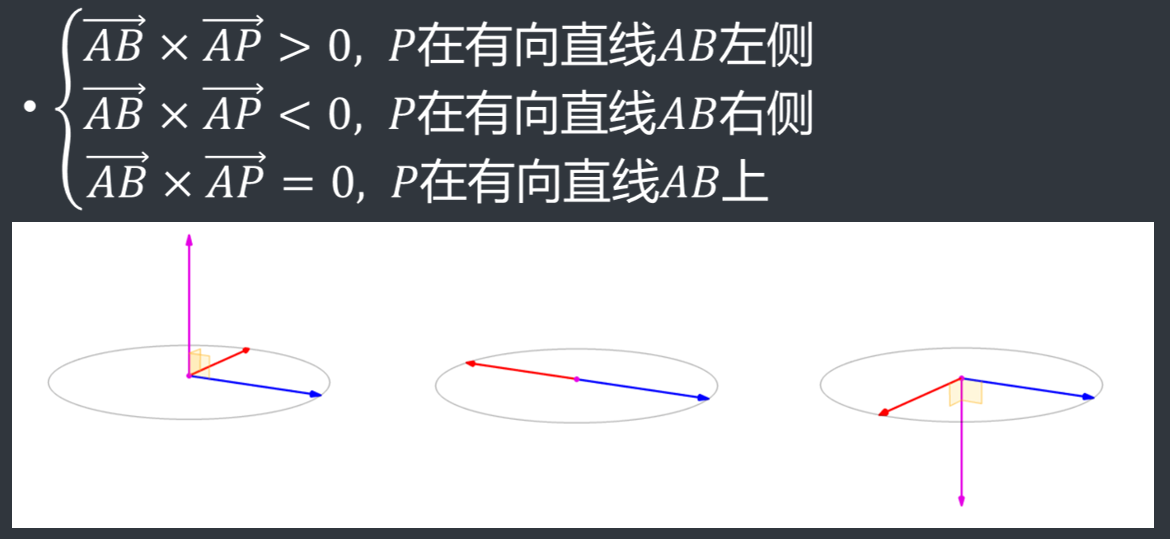
to-left测试
用途:判断一个点与一个直线的位置关系
与右手螺旋定则相似
向量的旋转
旋转的本质是线性变换
//指路3Blue1Brown

线段
记录两个端点(无向无序)
struct Segment{
Point a,b;
};
判断线段相交:
跨立实验
输入两条直线AB与CD,输出两者是否相交
点A和点B在直线CD的不同侧,点C和点D在直线的不同侧
warning:退化情况 三点/四点共线情况
直线
表示方式
- 斜截式/点斜式:k不存在时需要特判
- 截距式:过原点的直线均无法表示
- 一般式:Ax + By + C = 0,判断两个直线相交需要高斯消元,多个直线较难处理,一般不用
- 点向式:常用,使用一点和一个方向向量表示直线
也可以表示射线或者线段(对k进行限定)
struct Line{
Point p,v;
};
(x,y)=OP + kv;
点到直线的距离:
- 投影+勾股定理:误差大不建议(涉及开方),但是可以求B点坐标
- 利用叉积

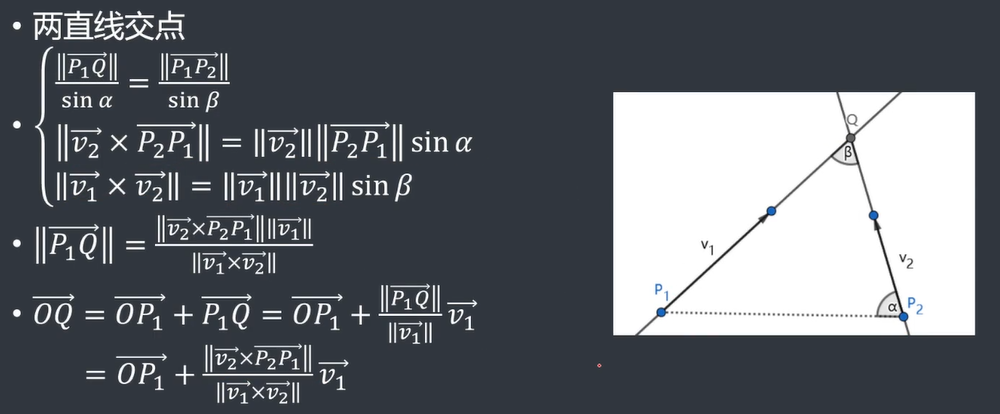
求两直线交点
思路:利用正弦定理和叉积,已知两个点和两个方向向量 = 已知三个内角度数和一个边长,求另外两个边长
多边形
多边形的表示:
本质:点的集合
struct Polygon{
vector<Point>p;
};
- 注意事项:
1.点的存储顺序要有序(一般采用逆时针顺序)
2.不一定满足凸性(可能是凹多边形)
3.注意对于第一个点和最后一个点的处理(比如边的对应)
多边形的面积
分解成若干三角形
三角剖分的思想
取平面内的一个点O
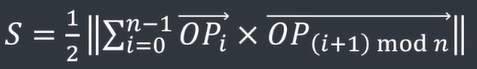
- warning:
1.注意取模的位置,先求和再取模
2.点的位置可以在多边形内和多边形外或多边形上均可
3.对于非凸多边形公示仍然适用
判断点是否在多边形的内部
方法一:to-left测试
即在所有边逆时针构成的直线的左侧
只对凸多边形适用
方法二:光线投射算法
从该点引出一条射线,该射线与多边形有奇数个交点则在内部,否则在外部
需要讨论特判与顶点相交的情况
方法三:回转数法
面内闭合曲线逆时针绕过该点的总次数
当回转数为零的时候该点在图形的外部
-
计算夹角的和—利用反三角函数
· 有精度和效率的问题 -
光线投射法的推广 O(n)
· 从该点做一条射线,如果图形的边是从下往上穿+1,从上往下穿-1,当结果为0的时候点在图形外部
一般选择水平射线
- warning:注意特判点在多边形上的情况,当顶点在射线上的时候认为该点在射线上侧然后对应判断上下穿
园
用圆心与半径进行表示
struct Circle{
Point c;
double r;
};


