BFS/DFS 广度/深度优先搜索
深度优先搜索DFS
所谓深度优先搜索,通俗点理解就是一条路走到头--不撞南墙不回头。
我们先来看一个全排列问题,现在要对1 2 3进行全排列,现在小哼手上拿着1 2 3三张卡片,他要将这三张卡片放入三个盒子里,每放满不就是一种全排列了么?
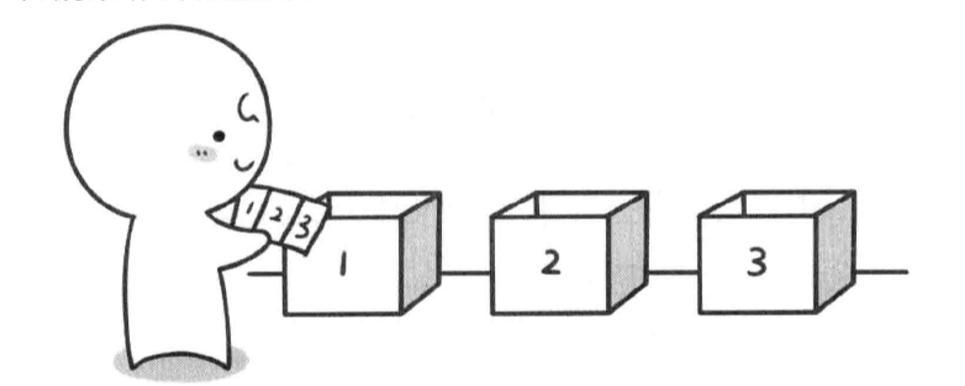
但是每次到底是先放卡片1还是卡片2,3呢?

小哼想,我按顺序放吧,每次都按照1.2.3的顺序放卡片。于是他走到1号盒子前把卡片1放入,走到2号盒子前把卡片2放入,走到3号盒子前把卡片3放入,走到四号盒子...但小哼的卡片已经放完
啦。这时就产生了一种全排列“1 2 3”啦。

但是还有好多种情况啊,于是产生了一种全排列后小哼要立即返回,他回到3号盒子前,将卡片3取回,看还能不能放其他卡片,显现小哼现在手里没除了卡片3外没有其他卡片了,所以小哼继续
往后退,到了2号盒子前,小哼将卡片2收回,这是小哼手里已经有两张卡片了,于是他将卡片3放入2号盒子,放好后又往后走一步来到三号盒子,将卡片2放入,又来到四号盒子前,当然没有
四号盒子啦,于是又产生了一种全排列“1 3 2”
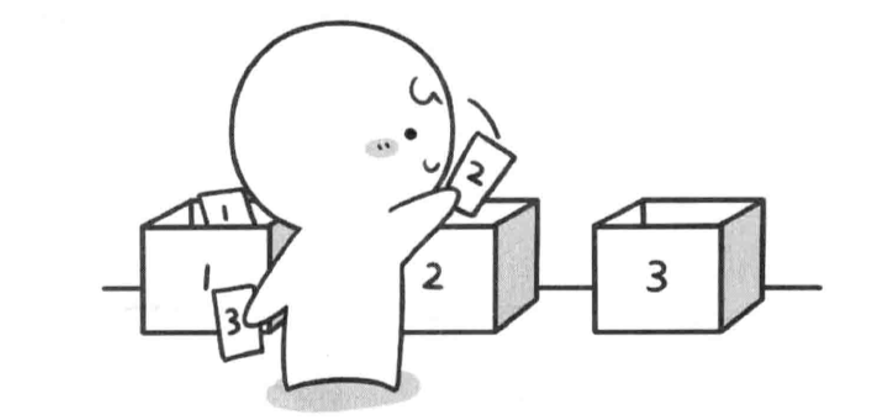
按照这样模拟后,便会依次生成全排列 “2 1 3” “2 3 1” “3 1 2” “3 2 1”
说了半天,我们看下如何用代码实现吧
先将i号卡片放入第step个盒子中
for(i = 1; i <=n; i++)
{
a[step] = i; //将卡片i放入第step个盒子里
}
但这里还有个问题,如何一张卡片已经放入其他盒子中了,就不能再放入当前的盒子中。所以,我们需要一个book[]数组来标记手上还有没有这张卡片
for(i = 1; i <= n; i++)
{
if(book[i] == 0) / /如果手上有这张卡片
{
a[step] = i; //将卡片i放入第step个盒子里
book[i] = 1; //此时手上已经没有这张卡了 标记一下
}
}
处理完第step个盒子后我们要向后走一步,处理第step+1个盒子,显然处理第step+1个盒子的方法和第step个盒子的一样,那么我们将刚才处理第step个盒子的方法写成一个函数
void dfs(int step)
{
for(i = 1; i <= n; i++)
{
if(book[i] == 0) / /如果手上有这张卡片
{
a[step] = i; //将卡片i放入第step个盒子里
book[i] = 1; //此时手上已经没有这张卡了 标记一下
}
}
}
处理第step+1个盒子只有dfs(step+1)就行啦
void dfs(int step)
{
for(i = 1; i <= n; i++)
{
if(book[i] == 0) / /如果手上有这张卡片
{
a[step] = i; //将卡片i放入第step个盒子里
book[i] = 1; //此时手上已经没有这张卡了 标记一下
}
dfs(step+1);//处理下个盒子
book[i] = 0; //这步很重要!!往回走时要将之前的卡片收回!
}
}
book[i] = 0;是将之前的卡片收回,如果不把刚才放入盒子的卡片收回,那么就无法再进行下一次摆放。
还剩最后一个问题,什么时候输出一个满足条件的序列呢?其实当我们走到第n+1个盒子前时,说明前n个盒子都已经放好卡片了,这时候我们就要return返回了
void dfs(int step)
{
if (step == n + 1) //判断边界
{
for (i = 1; i <= n; i++)
cout << a[i] << " ";
cout << endl;
return;//返回上一个盒子前
}
else
{
for (i = 1; i <= n; i++)
{
if (book[i] == 0) / /如果手上有这张卡片
{
a[step] = i; //将卡片i放入第step个盒子里
book[i] = 1; //此时手上已经没有这张卡了 标记一下
}
dfs(step + 1);//处理下个盒子
book[i] = 0; //这步很重要!!往回走时要将之前的卡片收回!
}
}
}
讲到这里想必大家已经对深度优先搜索有一定了解了吧,深搜使用就是递归和回溯的思想。
广度优先搜索BFS
讲完了dfs,我们再来看看什么是广度优先搜索。
所谓广度优先搜索就是一种层层递进的搜索。
我们来看一张图。这是一个迷宫,我们用一个二维数据储存它。
现在小哼站在(1 1)处,它可以向下或向右走,如何才能到达终点呢?已经学会深搜的你因该很快就想到办法了,但这里我们用另一种方法BFS,“一层层”扩展找到终点。扩展时每发现一个点就将这个点放入队列中,知道走到终点位置。和深搜一样,我们也需要一个book数组记录是否走过这个点。
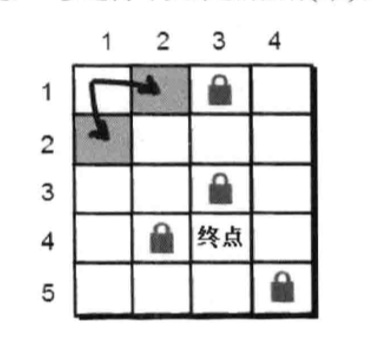
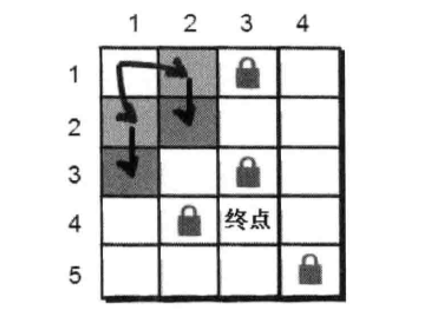
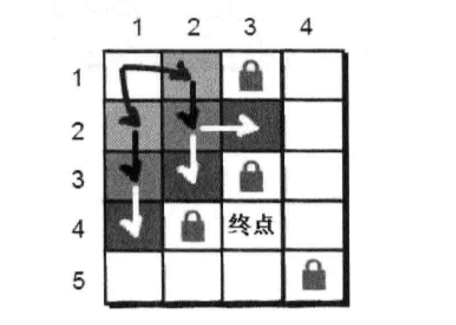
我们每对一个点扩展完毕,这个点就没用了,所以要将这个点出队,对下个点扩展。
理解了这点后代码就很容易实现了_。
完整代码
#include<bits/stdc++.h>
using namespace std;
struct node
{
int x, y;
int s;//步数
int f;//父亲再队列中的编号
};
int main()
{
queue<node> que;
int a[51][51] = { 0 };
int book[51][51] = { 0 };
int next[4][2] =
{
{0,1}, //向右走
{1,0},//向下走
{0,-1},//向左走
{-1,0}//向上走
};
int n, m, i, j, k, flag,p,q;
node start, tnode;
//输入迷宫的行列 起始点
cin >> n >> m >> start.x >> start.y;
//输入迷宫图
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
cin >> a[i][j];
cin >> p >> q;//输入终点
book[start.x][start.y] = 1;//将起始点标记为走过
//如果队列不为空
while (!que.empty())
{
//枚举四个方向
for (int k = 0; k <= 3; k++)
{
//计算下一步坐标
tnode.x = que.front().x + next[k][0];
tnode.y = que.front().y + next[k][1];
//判断是否出界
if (tnode.x<1 || tnode.x>n || tnode.y<1 || tnode.y>m)
continue;
//判断是否是陆地或已经走过
if (mapp[tnode.x][tnode.y] > 0 && book[tnode.x][tnode.y] == 0)
{
sum++;
//每个点只入队一次,标记走过
book[tnode.x][tnode.y] = 1;
int ts = que.back().s;//记录父亲的步数
//将该点入队
que.push(tnode);
que.back().s = ts+1; //步数是父亲步数加1
}
if (tnode.x == p && tnode.y == q)
{
flag = 1;
break;
}
}
if (flag == 1)
break;
que.pop();//队首出队
}
cout << que.back().s << endl;
system("pause");
return 0;
}
练习
学完DFS和BFS后来练习一下吧。
题目:宝岛探索
小哼通过一种秘密方法得到一张不完整的钓鱼岛航拍图。小哼决定去钓鱼岛探险。
下面的10*10的矩阵就是该航拍图。图中数字表示海拔,0表示海洋,1-9都表示陆地。
小哼的飞机会降落再(6,8),现在需要计算小哼降落岛的面积。此处我们把降落点上
下左右相邻岛视为同一岛屿。
输入

输出


BFS代码如下:
#include<bits/stdc++.h>
using namespace std;
struct node
{
int x;
int y;
};
int main()
{
queue<node> que;
int mapp[51][51];
int book[51][51];
int i, j, n, m,sum;
node start, tnode;
memset(book, 0, sizeof(book));
memset(mapp, 0, sizeof(mapp));
//输入地图的行列,初始坐标
cin >> n >> m >> start.x >> start.y;
//输入地图
for(i=1;i<=n;i++)
for (j = 1; j <= m; j++)
{
cin >> mapp[i][j];
}
int next[4][2]=
{
{0,1}, //向右走
{1,0},//向下走
{0,-1},//向左走
{-1,0}//向上走
};
//向队列插入降落的起始坐标
que.push(start);
sum = 1;
book[start.x][start.y] = 1;
//当队列不为空时循环
while (!que.empty())
{
//枚举四个方向
for (int k = 0; k <= 3; k++)
{
//计算下一步坐标
tnode.x = que.front().x + next[k][0];
tnode.y= que.front().y + next[k][1];
//判断是否出界
if (tnode.x<1 || tnode.x>n || tnode.y<1 || tnode.y>m)
continue;
//判断是否是陆地或已经走过
if (mapp[tnode.x][tnode.y] > 0 && book[tnode.x][tnode.y] == 0)
{
sum++;
//每个点只入队一次,标记走过
book[tnode.x][tnode.y] = 1;
//将该点入队
que.push(tnode);
}
}
//队首出队,下个点继续搜素
que.pop();
}
cout << sum << endl;
getchar();
getchar();
return 0;
}
DFS代码如下:
#include<bits/stdc++.h>
using namespace std;
struct node
{
int x;
int y;
};
int mapp[51][51];
int book[51][51];
int n, m,sum;
void dfs(int x,int y)
{
int next[4][2] =
{
{0,1}, //向右走
{1,0},//向下走
{0,-1},//向左走
{-1,0}//向上走
};
int tx, ty, k;
//枚举四个方向
for (k = 0; k <= 3; k++)
{
tx = x + next[k][0];
ty = y + next[k][1];
//判断是否出界
if (tx<1 || tx>n || ty<1|| ty>m)
continue;
//判断是否是陆地或已经走过
if (mapp[tx][ty] > 0 && book[tx][ty] == 0)
{
sum++;
//标记走过
book[tx][ty] = 1;
dfs(tx, ty); //执行下一步
}
}
return;
}
int main()
{
int i, j,sx,sy;
memset(book, 0, sizeof(book));
memset(mapp, 0, sizeof(mapp));
cin >> n >> m >> sx >> sy;
//输入地图
for(i=1;i<=n;i++)
for (j = 1; j <= m; j++)
{
cin >> mapp[i][j];
}
book[sx][sy] = 1;
sum = 1;
dfs(sx, sy);
cout << sum << endl;
getchar();
getchar();
return 0;
}
拓展:如何求有多少个独立岛屿呢?
即求独立子图的个数,这就是Floodfill漫水填充法,又叫种子填充法。Windows下“画图”中的油漆桶工具就是基于这个算法的。
我们将独立岛屿进行染色,所以增加参数color。
代码如下
#include<bits/stdc++.h>
using namespace std;
struct node
{
int x;
int y;
};
int mapp[51][51];
int book[51][51];
int n, m,sum;
void dfs(int x,int y,int color)
{
mapp[x][y] = color;//表示小哼来过这个岛
int next[4][2] =
{
{0,1}, //向右走
{1,0},//向下走
{0,-1},//向左走
{-1,0}//向上走
};
int tx, ty, k;
//枚举四个方向
for (k = 0; k <= 3; k++)
{
tx = x + next[k][0];
ty = y + next[k][1];
//判断是否出界
if (tx<1 || tx>n || ty<1|| ty>m)
continue;
//判断是否是陆地或已经走过
if (mapp[tx][ty] > 0 && book[tx][ty] == 0)
{
sum++;
//标记走过
book[tx][ty] = 1;
dfs(tx, ty,color); //执行下一步
}
}
return;
}
int main()
{
int i, j,sx,sy,color=0;
memset(book, 0, sizeof(book));
memset(mapp, 0, sizeof(mapp));
cin >> n >> m ;
//输入地图
for(i=1;i<=n;i++)
for (j = 1; j <= m; j++)
{
cin >> mapp[i][j];
}
//对每个大于0(未被染色)的点尝试dfs染色
for (i = 1; i <= n; i++)
{
for (j = 1; j <= m; j++)
{
if (mapp[i][j] > 0)//如果没被染色
{
color--;//color减一表示一种新的颜色
book[i][j] = 1; //标记走过
dfs(i, j, color);
}
}
}
for (i = 1; i <= n; i++)
{
for (j = 1; j <= m; j++)
{
cout<<mapp[i][j]<<" ";
}
cout << endl;
}
cout <<"共有独立岛屿:"<< -color<<" 个" << endl;
getchar();
getchar();
return 0;
}
题目描述
已知 n 个整数 x1,x2,…,xn,以及1个整数k (k<n)。从n个整数中任选k个整数相加,可分别得到一系列的和。例如当n=4,k=3,4个整数分别为3,7,12,19时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29
输入输出格式
输入格式:
键盘输入,格式为:
n,k (1≤n≤20, k<n)
x1,x2,…,xn (1≤xi≤5000000)
输出格式:
屏幕输出,格式为: 1个整数(满足条件的种数)。
输入输出样例
输入样例#1: 复制
4 3
3 7 12 19
输出样例#1: 复制
1
即每次从n可数字中选择k个不重复的数计算他们的和是否为质数。我们可以用dfs做,但要考虑去重的问题,所以要修改dfs中的for循环。
思路如下:因为不能重复,所以每次我们进行dfs下一步时只能从前一个数的下一个数开始选择,也就是for循环要从前一个数(假设位置为start)的start+1开始。
例如案列,我们用dfs每次选一个数累加,我们先选择3,dfs下一步,这时我们要从7开始,所以每次dfs时要把上一步i的值+1设为这部for循环的初始值。
#include<iostream>
using namespace std;
int k,ans = 0,n;
int a[25];
bool isPrime(int n) {
if (n <= 3) {
return n > 1;
}
for (int i = 2; i <= sqrt(n); i++) {
if (n%i == 0) {
return false;
}
}
return true;
}
void dfs(int step,int sum,int start) {
if (step == k ) {
//cout << sum << endl;
if (isPrime(sum)) {
ans++;
}
return;
}
for (int i = start; i < n; i++) {
dfs(step + 1, sum + a[i], i + 1);
}
}
int main() {
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
dfs(0,0,0);
cout << ans << endl;
system("pause");
return 0;
}
迷宫
【问题描述】
下图给出了一个迷宫的平面图,其中标记为 1 的为障碍,标记为 0 的为可
以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这
个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按DRRURRDDDR 的顺序通过迷宫,
一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫(30 行 50 列),请找出一种通过迷宫的方式,
其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中D<L<R<U。(如果你把以下文字复制到文本文件中,请务
必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt,
内容与下面的文本相同)
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
试题D: 迷宫 5
第十届蓝桥杯大赛软件类省赛 C/C++ 大学 A 组
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个字符串,包含四种字母 D、U、L、R,在提交答案时只填写这个字符串,填
写多余的内容将无法得分。
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<string.h>
#include<string>
#include<queue>
using namespace std;
struct node {
int x, y;
string road;
};
string str;
string a[30];
int visit[30][50];
void bfs(node start,node end) {
memset(visit, 0, sizeof(visit));
queue<node> que;
que.push(start);
int dir[][2] = {
{1,0},{0,-1},{0,1},{-1,0}
};
char ch[4] = { 'D','L','R','U' };
visit[start.x][start.y] = 1;
while (!que.empty()) {
node tmp = que.front();
que.pop();
if (tmp.x == end.x && tmp.y == end.y) {
cout << tmp.road << endl;
return;
}
for (int i = 0; i < 4; i++) {
int x = tmp.x + dir[i][0];
int y = tmp.y + dir[i][1];
if (x < 30 && y < 50 && visit[x][y] == 0 && x >= 0 && y >= 0&&a[x][y] == '0') {
visit[x][y] = 1;
node tmp2;
tmp2.x = x;
tmp2.y = y;
tmp2.road = tmp.road + ch[i];
que.push(tmp2);
}
}
}
}
int main() {
str = "01010101001011001001010110010110100100001000101010\
00001000100000101010010000100000001001100110100101\
01111011010010001000001101001011100011000000010000\
01000000001010100011010000101000001010101011001011\
00011111000000101000010010100010100000101100000000\
11001000110101000010101100011010011010101011110111\
00011011010101001001001010000001000101001110000000\
10100000101000100110101010111110011000010000111010\
00111000001010100001100010000001000101001100001001\
11000110100001110010001001010101010101010001101000\
00010000100100000101001010101110100010101010000101\
11100100101001001000010000010101010100100100010100\
00000010000000101011001111010001100000101010100011\
10101010011100001000011000010110011110110100001000\
10101010100001101010100101000010100000111011101001\
10000000101100010000101100101101001011100000000100\
10101001000000010100100001000100000100011110101001\
00101001010101101001010100011010101101110000110101\
11001010000100001100000010100101000001000111000010\
00001000110000110101101000000100101001001000011101\
10100101000101000000001110110010110101101010100001\
00101000010000110101010000100010001001000100010101\
10100001000110010001000010101001010101011111010010\
00000100101000000110010100101001000001000000000010\
11010000001001110111001001000011101001011011101000\
00000110100010001000100000001000011101000000110011\
10101000101000100010001111100010101001010000001000\
10000010100101001010110000000100101010001011101000\
00111100001000010000000110111000000001000000001011\
10000001100111010111010001000110111010101101111000";
int j = 0;
for (int i = 0; i < 30; i++) {
a[i] = str.substr(j, 50);
j += 50;
}
node start, end;
start.x = 0;
start.y = 0;
start.road = "";
end.x = 29;
end.y = 49;
end.road = "";
bfs(start, end);
system("pause");
return 0;
}



