判断点在多边形内 射线法详解

问题描述

现有一个点p（x0,y0）,多变形ptPolypon，判断点p是否在多边形内。

算法

判断一个点是否在多边形内，我们可以从该点引出一条水平射线（任意射线都可，但水平便于计算），观察射线与多变形的交点个数，如果交点个数为奇数，则该点在多边形内，如果为 偶数 则在多边形外。

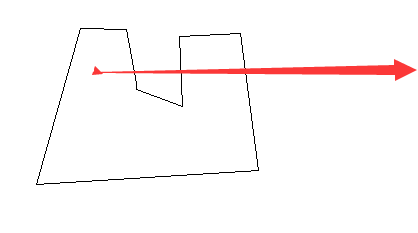
如图 点在多边形内，从该点做一条水平射线，与多边形交点个数为2*n+1 为奇数，同理若点在多变形外为偶数。

如何判断水平射线与多变形的边有交点呢？
显然，如果某条边是水平的，那么肯定没有交点
if (p1.y == p2.y) continue;

如果点p的纵坐标比多边形某边的纵坐标都小或都大，那么他们的交点一定在延长线上，如图所示

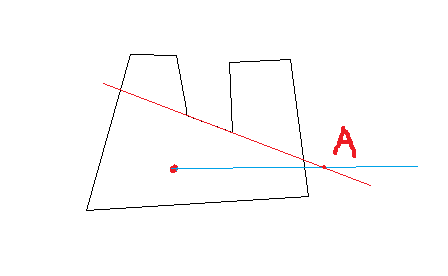
if (p.y < min(p1.y, p2.y))
			continue;
if (p.y >= max(p1.y, p2.y))
			continue;

接下来我们考虑一般情况。要想判断有没有交点，我们只需要将多边形某边所在直线的方程求出，将p点的纵坐标y0带入，即可求得交点横坐标x，将x与x0比较，如果下x0<x,该点在多边形内反之在多边形外。
公式为：

\[x = (y0- p1.y)*(p2.x - p1.x)/ (p2.y - p1.y)+ x0 \]

完整代码

struct Point
{
	double x, y;
};
bool IsInPolygon(Point p,Point *ptPolygon,int ncount)
{
	int ncross = 0;
	for (int i = 0; i < ncount; i++)
	{
		Point p1 = ptPolygon[i];
		Point p2 = ptPolygon[(i + 1) % ncount]; //相邻两条边p1,p2
		if (p1.y == p2.y)         
			continue;
		if (p.y < min(p1.y, p2.y))
			continue;
		if (p.y >= max(p1.y, p2.y))
			continue;
		double x = (p.y - p1.y)*(p2.x - p1.x) / (p2.y - p1.y) + p1.x;
		if (x > p.x)
			ncross++; //只统计单边交点
	}
	return(ncross % 2 == 1);
}