【算法】凸包问题--分治法
凸包问题--分治法
求能够完全包含平面上n个给定点的凸多边形。
示例:
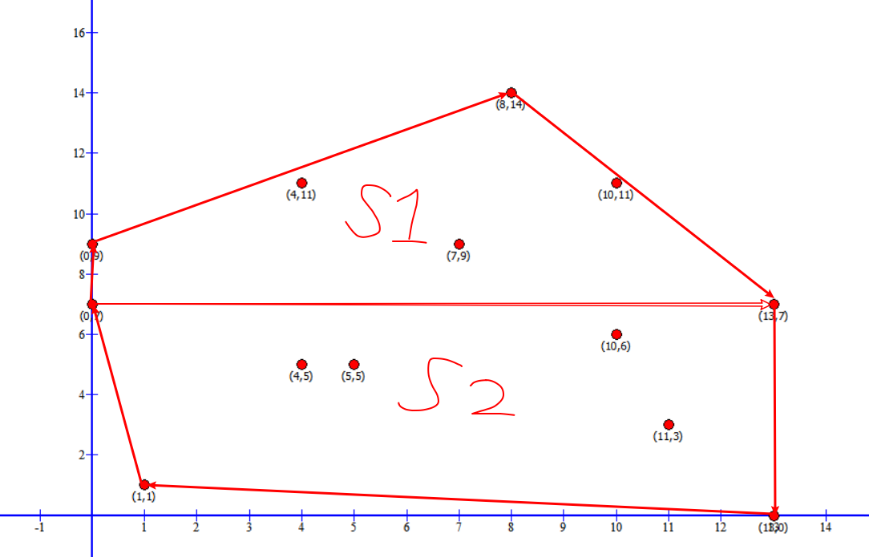
一、分治法:
(一)算法思路:
(这里所说的直线都是有向直线的。)
将数组升序排序,若x轴坐标相同,按照y轴坐标升序排序。
最左边的点p1和最右边的点p_n一定是该集合凸包的顶点。该直线将点分为两个集合,上包为S1,下包为S2。在p1 p_n线上的点不可能是凸包的顶点,所以不用考虑。
在上包S1中,找到p_max(距离直线p1p_n最远距离的点),若有两个距离同样远的点,取∠p_max p1 p_n最大的那个点(即△p_max p1 p_n面积最大)。
(一次递归到这里结束)
找出S1中所有在直线p1 p_max左边的点,这些点中一定有构成上包中左半部分边界的顶点,用上面的算法递归查找点,直到上包就是以p1和p_n为端点的线段。
下包S2中找下边界 同理。
*如何判断点是否在直线p1 p_max左边(同 p1 p_n上方)?
如果q1(x1,y1),q2(x2,y2),q3(x3,y3)是平面上的任意三个点,那么三角形△q1 q2 q3的面积等于下面这个行列式绝对值的二分之一。

当且仅当点q3=(x3,y3)位于直线q1 q2的左侧时,该表达式的符号为正,该点位于两个点确定的直线的左侧。
(二)实现中碰到的问题
-
如何用快速排序来排序Point类(内有坐标x,y)的一维数组?
按照x坐标排序很简单,若碰到x相同,y不同的怎么办?
在快排的原基础上修改,以j向前逼近说明:
(第一个while循环)当前比较数的横坐标>基准点的时,j向前逼近。此处不加等于号,排序是不稳定的,即相等元素的相对位置可能发生改变。(快排详见博客:https://www.cnblogs.com/musecho/p/11647349.html)
(第二个while为添加内容)比较相等元素的纵坐标,基准点的更小,j继续向前逼近,即相等元素的相对位置不发生改变;否则,则改变。也就是将原来快排中while循环拆分为两个,增加相等元素另外比较纵坐标的情况。
while (i < j && points[j].getX() > center.getX()) {
j--;
}
while (i < j && center.getX() == points[j].getX() && points[j].getY() > center.getY()) {
j--;
}
/*
* (i<j)若points[j].getX()< center.getX()或 center.getX() ==
* points[j].getX()且points[j].getY()<center.getY() 以上两种情况,需要赋值
*/
if (i < j)// 跳出循环也有可能时因为i=j,所以这里要判断一下
points[i++] = points[j];
- 如果使用全局数组visit标识点是否访问,能确定凸包的所有顶点,但怎么顺序输出?
在已经求的凸包顶点里逐一确定边界,判断是不是所有点都在这条边界的一侧,如果是则确定一条边界。
convexHullList.add(convexHullVertex[0]);// 开始点
int haveCount = 1;// 已经加入点的个数
// 逐条确定边界,判断是否除了该条假设边界上的点,其他凸包的顶点都在直线的右边。
// 如果是,则此条直线为边界;如果不是,取下一个边界终点,继续判断。
int start = 0;// 起点
for (int end = start + 1; haveCount < count;) {
boolean boundRight = true;
for (int i = 0; i < count; i++) {
while (i < count && (i == start || i == end)) {// 不能写if,start和end可能是连在一起的
i++;
}
if (i >= count)
break;
// 点在直线左侧或线上,错误
if (PointJudge(convexHullVertex[start], convexHullVertex[end], convexHullVertex[i]) >= 0) {
boundRight = false;
end = (end + 1) % count;// end取下一个
break;
}
}
if (boundRight == true) {
convexHullList.add(convexHullVertex[end]);
start = end;
end = (start + 1) % count;
haveCount++;
}
}
(三)注意点
-
注意方法PointJudge(Point beginP, Point endP,Point p)和PointCal(Point beginP,Point endP,Point p)中,传参放在第几个:
前两个点是直线的两端,第三个是需要判断的点
- 注意下包循环中的 起始点、终点、判断条件
for (int i = begin - 1; i >= end + 1; i--)
(四)源代码
1.ConvexHullProblem_DC
package ConvexHullProblem;
import java.util.ArrayList;
import java.util.Arrays;
/**
* 凸包问题(分治法):
*/
public class ConvexHullProblem_DC {
boolean[] visit;// 标志点是否是凸包的顶点:1是,0不是
Point[] points;// 所有点
Point[] convexHullVertex;// 凸包的顶点
ArrayList<Point> convexHullList = new ArrayList<>();;// 凸包的顶点(顺序存放)
public void ConvexHullProblem(Point[] points) {
this.points = points;
quickSort(0, points.length - 1);// 升序排序
// System.out.println("升序:" + Arrays.toString(points));
visit = new boolean[points.length];
recursion(0, points.length - 1);// 上包
recursion(points.length - 1, 0);// 下包
orderConvexHull();
}
/**
* @title: recursion
* @description: 在凸包的上包或下包中,找使△p_max p1 p_n面积最大的点p_max,并递归
* @date: 2019年10月16日 下午8:33:14
* @param begin 直线的起点
* @param end 直线的终点 void
* @throws:
*/
void recursion(int begin, int end) {
// 直线的两端点为凸包的顶点
visit[begin] = true;
visit[end] = true;
if (begin < end) {
boolean flag = false;// 标志直线左侧是否有点
int maxArea = 0;// 最大面积
int maxAreaindex = begin + 1;// 最大面积的点下标
for (int i = begin + 1; i <= end - 1; i++) {// begin和end已经是顶点,不需要判断
if (PointJudge(points[begin], points[end], points[i]) > 0) {// 点在直线左侧
// 找距离最远的点,因为底相同都是p1 pn,也就是求三角形面积最大的
flag = true;
int area = PointCal(points[begin], points[end], points[i]);
if (area > maxArea) {
maxArea = area;
maxAreaindex = i;
} else if (area == maxArea) {// 若面积相同,取∠p_max p_begin p_end最大的那一个
System.out.println(22);
double degreeA = Degree(points[begin], points[i], points[end]);
double degreeB = Degree(points[begin], points[maxAreaindex], points[end]);
if (degreeA > degreeB) {
maxArea = area;
maxAreaindex = i;
}
}
// System.out.println("area=" + area + ",Point=" + points[i]);
}
}
// System.out.println("maxArea=" + maxArea + ",Point=" + points[maxAreaindex]);
// System.out.println("over");
// 若直线左侧还有点,则递归;没有点,则结束
if (flag == true) {
recursion(begin, maxAreaindex);
recursion(maxAreaindex, end);
}
} else if (begin > end) {
boolean flag = false;
int maxArea = 0;// 最大面积
int maxAreaindex = end + 1;// 最大面积的点下标
for (int i = begin - 1; i >= end + 1; i--) {// 注意下包循环中的 起始点、终点、判断条件
if (PointJudge(points[begin], points[end], points[i]) > 0) {// 点在直线左侧
flag = true;
int area = PointCal(points[begin], points[end], points[i]);
if (area > maxArea) {
maxArea = area;
maxAreaindex = i;
} else if (area == maxArea) {// 若面积相同,取∠p_max p_begin p_end最大的那一个
System.out.println(22);
double degreeA = Degree(points[begin], points[i], points[end]);
double degreeB = Degree(points[begin], points[maxAreaindex], points[end]);
if (degreeA > degreeB) {
maxArea = area;
maxAreaindex = i;
}
}
// System.out.println("area=" + area + ",Point=" + points[i]);
}
}
// System.out.println("maxArea=" + maxArea + ",Point=" + points[maxAreaindex]);
// System.out.println("over");
if (flag == true) {
recursion(begin, maxAreaindex);
recursion(maxAreaindex, end);
}
}
}
/**
* @title: quickSort:运用Hoare
* @description: 快速排序: 选取第一个元素作为基准点(可以随机选取),将剩下元素与基准点进行比较,
* 比基准点大的放在右边,比基准点小的放在左边, 得到左子表和右子表,递归调用本函数;
* @param points 数组
* @param begin 开始下标
* @param end 结束下标
* @throws:
*/
void quickSort(int begin, int end) {
if (begin >= 0 && begin < end && end < points.length) {
int i = begin, j = end;
Point center = points[i];// 中心元素
while (i != j) {
while (i < j && points[j].getX() > center.getX()) {
j--;
}
while (i < j && center.getX() == points[j].getX() && points[j].getY() > center.getY()) {
j--;
}
/*
* (i<j)若points[j].getX()< center.getX()或 center.getX() ==
* points[j].getX()且points[j].getY()<center.getY() 以上两种情况,需要赋值
*/
if (i < j)// 跳出循环也有可能时因为i=j,所以这里要判断一下
points[i++] = points[j];
while (i < j && points[i].getX() < center.getX()) {
i++;
}
while (i < j && points[i].getX() == center.getX() && points[i].getY() < center.getY()) {
i++;
}
/*
* (i<j)若points[i].getX()> center.getX()或 center.getX() ==
* points[i].getX()且points[i].getY()>center.getY() 以上两种情况,需要赋值
*/
if (i < j)
points[j--] = points[i];
}
points[i] = center;// 中心元素到达最终位置
quickSort(begin, i - 1);
quickSort(i + 1, end);
}
}
/**
* @title: PointCal
* @description: 计算行列式的值
* @date: 2019年10月15日 下午7:53:07
* @param beginP 直线的开始点
* @param p 判断的点
* @param endP 直线的终点
* @return int 行列书的值
* @throws:
*/
private int PointCal(Point beginP, Point endP, Point p) {
int cal = 0;// 行列式值
//x1y2+x3y1+x2y3-x3y2-x2y1-x1y3
cal = beginP.getX() * endP.getY() + p.getX() * beginP.getY() + endP.getX() * p.getY() - p.getX() * endP.getY()
- endP.getX() * beginP.getY() - beginP.getX() * p.getY();
return cal;
}
/**
* @title: PointJudge
* @description:返回点p在直线beginP endP的位置
* @date: 2019年10月15日 下午7:56:56
* @param beginP
* @param p 判断的点
* @param endP
* @return int :1在直线左侧,0在线上,-1在右侧
* @throws: 注意传参放在第几个,前两个点是直线的两端,第三个是需要判断的点
*/
private int PointJudge(Point beginP, Point endP, Point p) {
if (PointCal(beginP, endP, p) > 0) {
return 1;
} else if (PointCal(beginP, endP, p) == 0)
return 0;
else
return -1;
}
/**
* @title: Degree
* @description: 余弦公式求∠pa pb pc的度数
* @date: 2019年10月16日 下午6:59:29
* @param pa 点
* @param pb
* @param pc
* @return double:返回∠c的度数(°为单位)
* @throws:
*/
double Degree(Point pa, Point pb, Point pc) {
double degree = 0;// ∠pa pb pc度数
// 三角形的三边长
double a = Math.sqrt(Math.pow(pa.getX() - pb.getX(), 2) + Math.pow(pa.getY() - pb.getY(), 2));
double b = Math.sqrt(Math.pow(pb.getX() - pc.getX(), 2) + Math.pow(pb.getY() - pc.getY(), 2));
double c = Math.sqrt(Math.pow(pc.getX() - pa.getX(), 2) + Math.pow(pc.getY() - pa.getY(), 2));
// 余弦公式求∠pa pb pc度数
System.out.println("acos=" + Math.acos((a * a + b * b - c * c) / (2.0 * a * b)));
degree = Math.toDegrees(Math.acos((a * a + b * b - c * c) / (2.0 * a * b)));
System.out.println("degree=" + degree);
return degree;
}
/**
*@title: orderConvexHull
*@description: 凸包顶点按顺时针输出
*@date: 2019年10月19日 上午9:28:44
*void
*@throws:
*/
void orderConvexHull() {
/** 将凸包顶点存放进另一个数组 */
int count = 0;// 凸包的顶点个数
for (int i = 0; i < visit.length; i++) {
if (visit[i] == true) {
count++;
}
}
convexHullVertex = new Point[count];
for (int j = 0, i = 0; j < visit.length; j++) {
if (visit[j] == true) {
convexHullVertex[i] = points[j];
i++;
}
}
convexHullList.add(convexHullVertex[0]);// 开始点
int haveCount = 1;// 已经加入点的个数
// 逐条确定边界,判断是否除了该条假设边界上的点,其他凸包的顶点都在直线的右边。
// 如果是,则此条直线为边界;如果不是,取下一个边界终点,继续判断。
int start = 0;// 起点
for (int end = start + 1; haveCount < count;) {
boolean boundRight = true;
for (int i = 0; i < count; i++) {
while (i < count && (i == start || i == end)) {// 不能写if,start和end可能是连在一起的
i++;
}
if (i >= count)
break;
// 点在直线左侧或线上,错误
if (PointJudge(convexHullVertex[start], convexHullVertex[end], convexHullVertex[i]) >= 0) {
// System.out.println("****");
// System.out.println(convexHullVertex[start]);
// System.out.println(convexHullVertex[end]);
// System.out.println(convexHullVertex[i]);
// System.out.println("****");
boundRight = false;
end = (end + 1) % count;// end取下一个
break;
}
}
if (boundRight == true) {
convexHullList.add(convexHullVertex[end]);
start = end;
end = (start + 1) % count;
haveCount++;
}
}
convexHullList.add(convexHullVertex[0]);// 结束点
System.out.println("凸包顶点顺时针输出:" + convexHullList);
}
}
2.Point
package ConvexHullProblem;
/**
* 点的信息
*/
public class Point {
private int x, y;// 横纵坐标
public Point(int x,int y) {
this.x=x;
this.y=y;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
public String toString() {
return " (" + x + ", "+ y + ")";
}
}
3.Demo_DC
package ConvexHullProblem;
import java.util.Arrays;
import java.util.Scanner;
public class Demo_DC {
public static void main(String[] args) {
//示例
Point[] points=new Point[13];
points[0] = new Point( 4, 5);
points[1] = new Point(10, 11);
points[2] = new Point( 4, 11);
points[3] = new Point( 1, 1);
points[4] = new Point( 10, 6);
points[5] = new Point( 8, 14);
//横坐标最两侧的点
points[6] = new Point( 13, 7);
points[7] = new Point( 13, 0);
points[8] = new Point( 0, 9);
points[9] = new Point( 0, 7);
points[10] = new Point( 5, 5);
points[11] = new Point( 7, 9);
points[12] = new Point( 11, 3);
// Scanner scanner = new Scanner(System.in);
// System.out.println("**********凸包问题**********");
// System.out.println("请输入点的数量:");
// int n = scanner.nextInt();
// Point[] points = new Point[n];
// points = randomPoint(points);
System.out.println("随机生成点:" + Arrays.toString(points));
ConvexHullProblem_DC convexHullProblem = new ConvexHullProblem_DC();
convexHullProblem.ConvexHullProblem(points);
}
static Point[] randomPoint(Point[] points) {
for (int i = 0; i < points.length; i++) {
int x = (int) (Math.random() * 21);// [0-20]
int y = (int) (Math.random() * 21);// [0-20]
points[i] = new Point(x, y);
}
return points;
}
}
(运行结果)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号