bzoj3622 ( 容斥，二项式反演)

https://vjudge.d0j1a1701.cc/problem/黑暗爆炸-3622

直接考虑每个人至少一个物品不好想，反过来考虑恰好0人没有物品。
f(i)表示钦定i个人没有物品，f(i)= \(\left(\begin{array}{c} n \\ i \end{array}\right) \prod_{j=1}^{m}\left(\begin{array}{c} n-i+a_{j}-1 \\ a_{j} \end{array}\right) 。\)
即从n个人中选i个不发物品，其他n-i个"随意"。 随意的意思是其他人有没有物品都行，是m个相同小球方n个不同盒子可以空盒的模型
二项式反演得到恰好0人没有物品

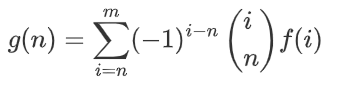
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false) ,cin.tie(0), cout.tie(0);
//#pragma GCC optimize(3,"Ofast","inline")
#define ll long long
//#define int long long
const int N = 2e3 + 5;
const int M = 1e3 + 5;
const int INF = 0x3f3f3f3f;
const ll LNF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double PI = acos(-1.0);
const double eps = 1e-13;
const int MATN = 102;
ll F[N];ll inv[N];
ll qmi(ll m, ll k) {
    ll res = 1;
    while(k) {
        if(k & 1) res = res * m % mod;
        m = m * m % mod;
        k >>= 1;
    }
    return res;
}
void init(int n){
    F[0]=inv[0]= 1;
    for(int i=1;i<=n;i++)F[i]=F[i-1]*i%mod;//求阶乘
    inv[n]=qmi(F[n],mod - 2);//随便求一下n的逆元
    for(int i=n-1;i>=1;i--)inv[i]=inv[i+1]*(i+1)%mod;//由最后一个往前推
}
ll C(ll n, ll m) {
    return F[n] * inv[m] % mod * inv[n - m] % mod;
}
ll num[1005];
int main() {
    IOS
    init(2000);
    int n, m; cin >> n >> m;
    for ( int i = 1; i <= m; ++ i ) {
        cin >> num[i];
    }
    ll ans = 0; ll t = -1;
    for ( int j = 0; j <= n; ++ j ) {
        if(j & 1) t = -1; else t = 1;
        ll tmp = t * C(n, j) % mod;
        for ( int i = 1; i <= m; ++ i ) {
            tmp = tmp * C(num[i] + n - j - 1, num[i]) % mod;
        }
        ans = (ans + tmp) % mod;
    }
    cout << (ans + mod) % mod << '\n';
    return 0;
}