AtCoder Beginner Contest 254 F (线段树求区间gcd)

https://atcoder.jp/contests/abc254/tasks/abc254_f
题意： 查询子矩阵的所有元素的gcd
思路：
首先要知道gcd的一个性质：

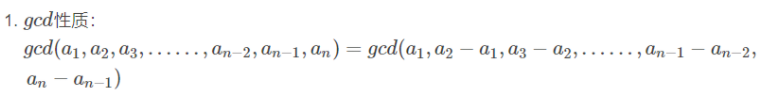
那么求h1w1，h2w2的矩阵gcd就等价 gcd( a[h1] + b[w1], gcd[ a[h1 + 1], a[h2]], gcd[ b[w1 + 1], b[w2]])
然后粘一个线段树求gcd板子

#include<bits/stdc++.h>
//#include <bits/extc++.h>
using namespace std;
// using namespace __gnu_cxx;
// using namespace __gnu_pbds;
#define IOS ios::sync_with_stdio(false) ,cin.tie(0), cout.tie(0);  
//#pragma GCC optimize(3,"Ofast","inline")
#define ll long long
#define ull unsigned long long
#define li __int128_t
#define PII pair<int, int>
#define re register
//#define int long long
const int N = 2e5 + 5;
const int M = 1e6 + 5;
const int mod = 1e9 + 7;
const ll LNF = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll a[N], b[N], ca[N], cb[N];
struct SegTree{
    ll g;
}tra[N<<2], trb[N<<2];
ll gcd(ll a,ll b){
    if(a<0) a=-a; if(b<0) b=-b;
    return b?gcd(b,a%b):a;
}

void push_up(int rt, SegTree *tree){
    tree[rt].g = gcd(tree[rt<<1].g,tree[rt<<1|1].g);
}
void tree_build(int l ,int r,int rt,ll *a, SegTree *tree){

    if(l==r){tree[rt].g=a[l] ;return ;}
    int mid = l+r>>1;
    tree_build(l,mid,rt<<1, a, tree);
    tree_build(mid+1,r,rt<<1|1, a, tree);
    push_up(rt, tree);
}

ll query(int a,int b,int l ,int r,int rt, SegTree *tree)
{
    if(l>b||r<a)return 0;
    if(l>=a&&r<=b)
    return tree[rt].g;
    int mid=l+r>>1;
    return gcd(query(a,b,l,mid,rt<<1, tree),query(a,b,mid+1,r,rt<<1|1, tree));
}
int main() {
  IOS
  int n, q;
  cin >> n >> q;
  for ( int i = 1; i <= n; ++ i ) cin >> a[i], ca[i] = a[i] - a[i - 1];
  for ( int i = 1; i <= n; ++ i ) cin >> b[i], cb[i] = b[i] - b[i - 1];

  tree_build(1,n,1,ca, tra); tree_build(1,n,1,cb,trb);
  while( q -- ) {
    int h1, h2, w1, w2; cin >> h1 >> h2 >> w1 >> w2;
    ll ans = a[h1] + b[w1];
    if( h1 + 1 <= h2 ) ans = gcd( ans, query(h1+1,h2,1,n,1, tra) );
    if( w1 + 1 <= w2 ) ans = gcd( ans, query(w1+1,w2,1,n,1, trb) );
    cout << ans << "\n";
  }

  return 0;
}