ABC249 E (奇怪状态，转移优化，线性DP)

https://atcoder.jp/contests/abc249/submissions/me

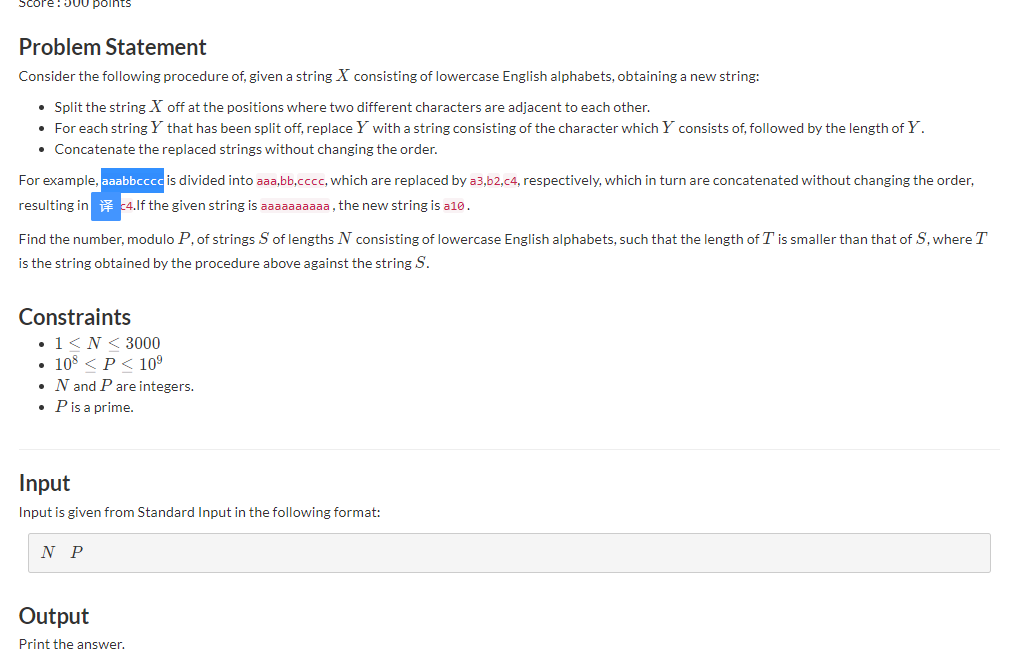
给你要生成的字符串长度和模数。问只用26个小写字母可以生成多少种字符串，且这个字符串进行合并操作后比原串长度小。

• 因为只给了规模要我们生成，所以dp只和同一字母的长度有关
• 根据题意设状态dp[i][j] 表示操作前的字符串长度i，操作后变为j
• 我们需要三重循环枚举i，枚举就， 枚举t：之前状态加上连续t长度的字母。
• 注意到 i前进长度1- 9的段对应j前进10 -99 ，N范围3000，所以j最多前进5
• 所以第三重循环枚举j前进多少，前缀和维护dp值，一个j前进对应一个区间和的i前进

#include<bits/stdc++.h>
#define ll long long
const int N = 3e3 + 5;
using namespace std;
ll f[N][N], sum[N][N];
int lg(int x) { int res = 1; while(x) ++ res, x /= 10; return res; }
void solve() {
    int n, p; cin >> n >> p;
    for ( int i = 1; i <= n; ++ i ) f[i][lg(i)] = 26;
    for ( int i = 1; i <= n; ++ i ) {
        for ( int j = lg(i) + 1; j <= min(i << 1, n); ++ j ) {
            for ( int t = 1, k = 2; t <= i; t *= 10, ++ k ) {
                f[i][j] += (((sum[i - t][j - k] - sum[i - min(i, t * 10)][j - k]) % p + p) % p) * 25 % p;

            }
        }
        for(int j=2;j<=n;j++) sum[i][j]=(sum[i-1][j]+f[i][j])%p;
    }
    ll ans = 0;
    for ( int i = lg(n); i < n; ++ i) ans = (ans + f[n][i]) % p;
    cout << ans << endl;
}
int main () {
    int t = 1; //cin >> t;
    while(t --) {
        solve();
    }
    return 0;
}