Luogu P3338 [ZJOI2014]力 （卷积 FFT）（紫）

卷积

对于一个\(O(n^2)\)的式子，如果可以化成卷积的形式，那么就能使用FFT，NTT等优化到\(O(nlogn)\)
卷积的离散形式：\((f * g)(n)=\sum_{i=-\infty}^{\infty} f(i) g(n-i)\)
对应到数组中fg[n]为g数组reverse一下，再与f数组一一对应下标相加，值相乘的结果。

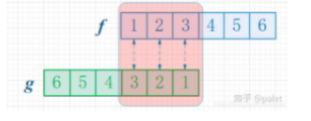
P3338

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false) ,cin.tie(0), cout.tie(0);
//#pragma GCC optimize(3,"Ofast","inline")
#define ll long long
const int N = 4e5 + 5;
const double PI = acos(-1.0);
int n;
int limit, L, RR[N];
struct Complex {
    double x, y;
    Complex operator+ (const Complex &t) const { return {x + t.x, y + t.y}; };
    Complex operator- (const Complex &t) const { return {x - t.x, y - t.y}; };
    Complex operator* (const Complex &t) const  { return {x * t.x - y * t.y, x * t.y + y * t.x}; };
}A[N], B[N], C[N];
void FTT(Complex * a, int type) {
    for ( int i = 0; i < limit; ++ i ) if(i < RR[i]) swap(a[i], a[RR[i]]);
    for ( int mid = 1; mid < limit; mid <<= 1) {
        Complex wn = {cos(PI/mid), type * sin(PI/mid)};
        for ( int pos = 0; pos < limit; pos += mid * 2) {
            Complex w = {1, 0};
            for ( int j = 0; j < mid; ++ j, w = w * wn) {
                Complex x = a[pos + j], y = w * a[pos + j + mid];
                a[pos + j] = x + y;
                a[pos + j + mid] = x - y;
            }
        }
    }
    if(type == - 1) {
        for ( int i = 0; i < limit; ++ i ) a[i].x /= limit;
    }
}
int main () {
    scanf("%d", &n);
    for ( int i = 1; i <= n; ++ i) {
        scanf("%lf", &A[i].x); C[n - i]. x = A[i].x;
        B[i].x = 1.0 / i / i;
    } //A[0] = B[0] = C[0] = {0, 0}; 傻逼C有值

    for ( limit = 1, L = 0; limit <= (n << 1); limit <<= 1, ++ L);
    for ( int i = 0; i < limit; ++ i ) RR[i] = (RR[i >> 1] >> 1) | ( (i & 1) << (L - 1) );
    FTT(A, 1); FTT(B, 1); FTT(C, 1);
    for ( int i = 0; i < limit; ++ i ) A[i] = A[i] * B[i];
    for ( int i = 0; i < limit; ++ i ) C[i] = C[i] * B[i];
    FTT(A, -1); FTT(C, -1);
    for ( int i = 1; i <= n; ++ i ) printf("%.4lf\n", A[i].x - C[n - i].x);

    return 0;
}