Acwing372. 棋盘覆盖 (匈牙利算法)

二分图最大匹配
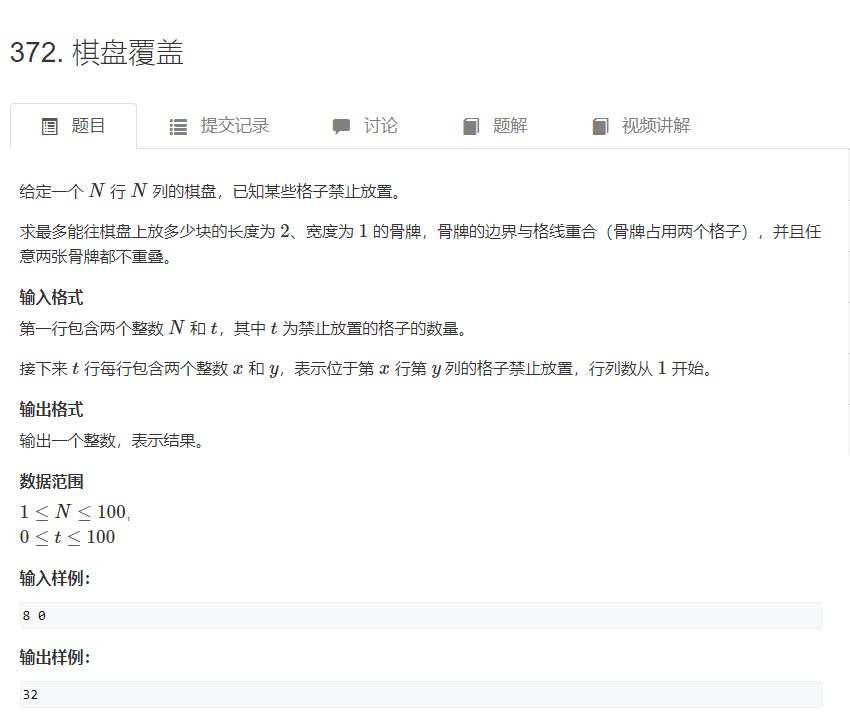
最多取多少条边,满足卡片不重叠--所有选出的边没有公共点--二分图放最多的牌--找到最多的边--二分图上最大匹配。
一条直线的两个端点要被分到两个集合，x+y值是奇数的在一个集合，是偶数的在一个集合。然后二分图最大匹配就行了，每次扫奇数点

#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N = 102;

bool g[N][N]; int n, m;
pair<int, int> match[N][N];
bool st[N][N];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
bool dfs(int x, int y) {
	for ( int i = 0; i < 4; ++ i ) {
		int nx = dx[i] + x, ny = dy[i] + y;
		if (nx && nx <= n && ny && ny <= n && !g[nx][ny] && !st[nx][ny]) {
			st[nx][ny] = 1;
			pair<int, int> t = match[nx][ny];
			if(t.x == -1 || dfs(t.x, t.y)) {
				match[nx][ny] = {x, y}; return true;//只用存第二个集合匹配第一个集合的哪个点 
			}
		}
	}
	return false;
}
int main () {
	cin >> n >> m; 
	while( m -- ) {
		int x, y; cin >> x >>y;
		g[x][y] = true;
	}
	memset(match, -1, sizeof match);
	int ans = 0;
	for ( int i = 1; i <= n; ++ i ) {
		for ( int j = 1; j <= n; ++ j ) {
			if((i + j) % 2 && !g[i][j]) {
				memset(st, 0, sizeof st);
				if(dfs(i, j)) ++ ans;
			}
		} 
	}
	cout << ans << endl;
	return 0;
}