【算法学习】动态规划的斜率优化
动态规划的状态转移方程为\(dp[i] = min(dp[j] + f(i,j)) , L(i)<=j<=R(i)\)
若\(f(i,j)\)仅与i,j中的一个有关,则可以采用单调队列优化,若\(f(i,j)\)与\(i,j\)均有关,则可以采用斜率优化
模板题
HDU3507
容易写出状态转移方程:
\(dp[i] = min(dp[j] + (s[i] - s[j])^2) + m , 0=<j<i\)
枚举一遍i,枚举一遍j的话时间复杂度是 \(n^2\)
使用斜率优化可以做到\(On\)
上面方程变换后,可看成一元线性方程y=kx+b:
\(dp[j]+s[j]^2=2s[i]*s[j]+dp[i]-s[i]^2-m\)
\(y = dp[j]+s[j]^2 , k =2s[i],x = s[j],b=dp[i]-s[i]^2-m\)
在二维坐标系考虑决策:
我们要求dp[i]最小,即b最小。 每一个决策j对应坐标系中的一个点\((s[j],dp[j]+s[j]^2)\)
将直线y=kx+b自下向上平移,第一次接触到的决策点b最小,就是最小的dp[i]
采用单调队列时需要注意两个问题:
1.处理过时决策点
枚举i ,斜率k是递增的,当前最优决策左侧的点已经过时,所以每次都将相邻两点线段斜率小于等于k的过时决策出队。这样队头就是最优决策
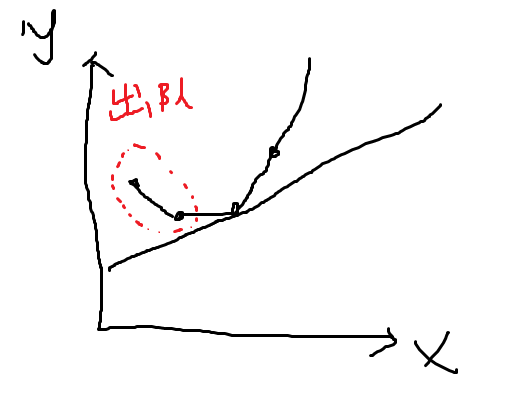
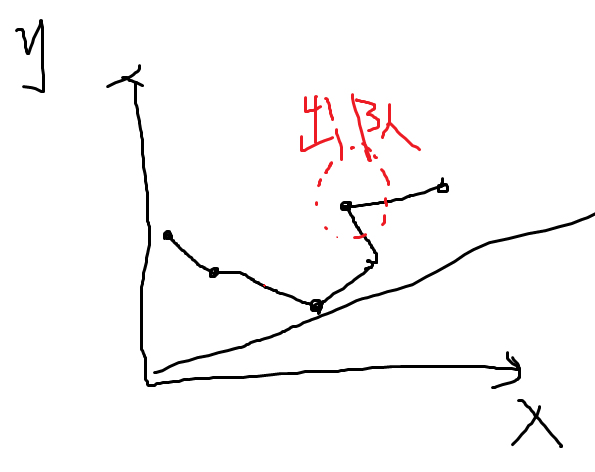
2.维护下凸壳
横坐标s[j]随着j的递增而递增,因此新的决策必然出现在下凸壳最右端。所以检查队列尾部两个点和第i个点是否下凸,若不满足,则队尾出队,直到满足,将i加入队列尾部。
点击查看代码
int n,m,c[N];
int dp[N],q[N];
int GetY(int k1,int k2){
return dp[k2]+c[k2]*c[k2]-(dp[k1]+c[k1]*c[k1]);
}
int GetX(int k1,int k2){
return c[k2]-c[k1];
}
int GetVal(int i,int j){
return dp[j]+(c[i]-c[j])*(c[i]-c[j])+m;
}
void solve(){
c[0] = 0; dp[0] = 0;
for(int i=1;i<=n;i++) scanf("%d",&c[i]) , c[i] += c[i-1];
int hh = 0,tt = - 1;
q[++tt] = 0;
for(int i=1;i<=n;i++){
while(hh< tt && GetY(q[hh],q[hh+1]) <= 2*c[i]*GetX(q[hh],q[hh+1])) ++hh;
dp[i] = GetVal(i,q[hh]);
while(hh< tt && GetY(q[tt],i)*GetX(q[tt-1],q[tt])<=GetY(q[tt-1],q[tt])*GetX(q[tt],i)) --tt;
q[++tt] = i;
}
printf("%d\n",dp[n]);
}
int main(){
while (~scanf("%d%d",&n,&m)){
solve();
}
return 0;
}
斜率优化&逆向dp
POJ1180
设\(dp[i][j]\)表示前i个作业被分成j批,前i-1个作业被分成j-1批的成本。
容易写出状态方程:
sumT[i]表消耗时间前缀和,sumF[i]是系数前缀和
\(dp[i][j]=dp[k][j-1]+(S*j+sumT[i])*(sumF[i]-sumF[k])\)
枚举i,j,k时间复杂度\(On^3\)
若不枚举j,而前面分段的时间会影响后面,为了取消后效性,进行逆向dp
sumT[i],sumF[i]改为后缀和
状态方程变成:
\(dp[i] = min(dp[j]+(sumT[i]-sumT[j]+S)*sumF[i]))\)
形如\(dp[i] = min(dp[j]+f(i,j))\)的递推式。移项,用斜率dp解决
点击查看代码
ll F[N],T[N],q[N],dp[N],s,n;
ll GetY(int a,int b){
return - dp[b] + dp[a];
}
ll GetX(int a,int b){
return - T[b] + T[a];
}
ll GetVal(int i,int j){
return dp[j] +(s+T[i]-T[j])*F[i];
}
ll GetK(int i){
return F[i];
}
void solve(){
for(int i=1;i<=n;++i) cin>>T[i]>>F[i];
for(int i=n-1;i>=1;--i) T[i]+=T[i+1],F[i]+=F[i+1];
int hh = 0,tt = -1;
q[++tt] = 0;
for(int i=n;i>=1;--i){
while(hh < tt && GetY(q[hh+1],q[hh])<=GetK(i)*GetX(q[hh+1],q[hh])) ++hh;
dp[i] = GetVal(i,q[hh]);
while(hh < tt && GetY(q[tt-1],q[tt])*GetX(q[tt],i)>=GetY(q[tt],i)*GetX(q[tt-1],q[tt])) --tt;
q[++tt] = i;
}
cout<<dp[1]<<endl;
}
int main() {
while (scanf("%d%d", &n, &s) != EOF) {
solve();
}
return 0;
}
虽然不是斜率优化,但是是二维单调队列
2020东北地区赛
毒气区只经过,我们不考虑。
\(f(i,j) = max(dp[i`][j`] + a[i][j])\) dist<=1
\(f(i,j) = max(dp[i`][j`] + a[i][j] -U)\) dist<=k
然后做二维单调队列,时间复杂度O(N*M)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);
using namespace std;
const int N = 1e3+5;
typedef long long ll;
ll g[N][N];
int n,m,k,u;
struct node{
int pos; ll val;
};
//col计算列最大值 , row计算前缀矩阵最大值
deque<int> col[N]; deque<node> row;
ll dp[N][N];
void solve(){
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin >> g[i][j],dp[i][j]=-1;
for(int i=1;i<=m;i++) col[i].clear();
dp[1][1] = g[1][1];
for(int i=1;i<=n;i++){
row.clear();
for(int j=1;j<=m;j++){
//更新队头
while (col[j].size() && col[j].front() < i - k) col[j].pop_front();//注意这题的k是个啥啊
while (row.size() && row.front().pos < j - k) row.pop_front();
//更新dp
if(g[i][j]>0){
//更新当前矩阵的最值
if(col[j].size()){
while (row.size() && row.back().val <= dp[col[j].front()][j]) row.pop_back();
row.push_back({j,dp[col[j].front()][j]});
}
//更新dp
if(row.size()) dp[i][j] = max(dp[i][j],row.front().val-u+g[i][j]);
//还原
if(col[j].size()) row.pop_back();
if (dp[i - 1][j] != -1) dp[i][j] = max(dp[i][j],dp[i - 1][j] + g[i][j]);
if (dp[i][j - 1] != -1) dp[i][j] = max(dp[i][j],dp[i][j - 1] + g[i][j]);
if (dp[i - 1][j - 1] != -1) dp[i][j] = max(dp[i][j],dp[i - 1][j - 1] + g[i][j]);
}
//更新队尾
if(dp[i][j] >= u){
while (col[j].size() && dp[col[j].back()][j] <= dp[i][j]) col[j].pop_back();
col[j].push_back(i);
}
if(col[j].size()){
while (row.size() && row.back().val <= dp[col[j].front()][j]) row.pop_back();
row.push_back({j,dp[col[j].front()][j]});
}
}
}
cout<<dp[n][m]<<endl;
}
int main(){
IOS
memset(dp,-1,sizeof dp);
while(cin>>n>>m>>k>>u){
solve();
}
return 0;
}



